Signaux physiques (PCSI)/Propagation d'un signal : Exemples de signaux, spectre

Signal mécanique transversal ou longitudinal, célérité de propagation

Déplacement d'un ébranlement le long d'une corde sur une petite durée

Déplacement d'une compression ponctuelle le long d'un ressort sur une petite durée

Modèle:AlUn signal mécanique est, a priori, une perturbation de courte durée se propageant dans un milieu matériel élastique en provoquant des déformations $($ ou ébranlements $)$ du milieu à son passage mais sans déplacement global de matière ;

Modèle:Alon distingue :

les signaux transversaux : ce sont des déformations orthogonales à la direction de propagation Modèle:Nobr la déformation d'une corde $($ ci-contre à gauche $)$ , une vague à la surface de l'eau $-$ exemple observable sur une cuve à ondes $\dots}$ ;
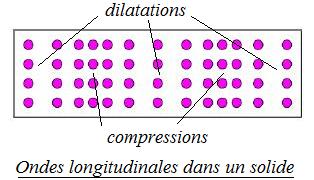
les signaux longitudinaux : ce sont des déformations parallèles à la direction de propagation Modèle:Nobr l'ensemble « compression et élongation » d'un ressort $($ ci-dessous à droite $)$ $\dots}$ .

Modèle:AlOn définit la célérité de propagation du signal mécanique notée $c$ comme la vitesse $($ non algébrisée $)$ de déplacement de la déformation mécanique c.-à-d. Modèle:Nobr

Grandeurs vibrantes en acoustique, célérité de la propagation

Modèle:AlUn signal acoustique est un signal mécanique dans un milieu matériel élastique fluide ^[1] ou solide, correspondant à une variation locale de pression ;
Modèle:Alce signal est nécessairement longitudinal dans un fluide^[1], mais longitudinal ou transversal dans un solide ^[2].

Notion de pression en mécanique

Modèle:AlQuand on exerce une force $\vec{F}$ sur un objet répartie sur une surface $S$ de l'objet, on peut décomposer cette force en une composante normale $F_{n} \vec{n}$ ^[3] et une composante tangentielle $F_{τ} \vec{τ}$ ^[4], seule la composante normale « appuie » sur l'objet, la composante tangentielle ayant tendance à déplacer l'objet tangentiellement ;

Modèle:Alla « composante normale $F_{n} \vec{n}$ est appelée force pressante » $($ cette dernière est effectivement pressante si $F_{n}$ est $> 0)$ et
Modèle:Alon définit la « pression exercée par la force pressante sur l'objet par la relation $p = \frac{F_{n}}{S}$ exprimée en $P a$ » $(1 P a = 1 N \cdot m^{- 2})$ ^[5].

Les deux principales grandeurs vibrantes en acoustique

Modèle:AlDans le cas d'un liquide « normal »^[6] ou un gaz, le signal acoustique est longitudinal, exemple :

Modèle:Al Modèle:Transparentun signal acoustique dans l'air où on observe la propagation par « compression ou dilatation » de « couches » d'air, la grandeur acoustique étant :

Modèle:Al Modèle:Transparent $≻$ l'« élongation $ξ$ de la couche d'air » c.-à-d. son déplacement par rapport à sa position au repos $($ voir ci-dessous
Modèle:Al Modèle:Transparent $≻$ à gauche $)$ ou, ce qui est une conséquence de la compression ou dilatation,
Modèle:Al Modèle:Transparent $≻$ la pression acoustique $p$ $($ ou pression relative voir le diagramme temporelle ci-dessous à droite $)$ « $p = P - P_{0}$ », $P_{0}$ étant la pression au repos et $P$ la pression instantanée, avec $p > 0$ pour une compression et $p < 0$ pour une dilatation.

Propagation du déplacement d'un piston à l'extrémité d'un tuyau rempli d'air
Propagation d'une surpression créée à l'extrémité d'un tuyau rempli d'air

Modèle:AlDans le cas d'un solide ou d'un liquide « très visqueux »^[7] le signal peut être :

longitudinal $($ onde $L)$ , exemple d'un signal acoustique $L$ dans l'acier à $1 %$ de carbone où on observe une succession de dilatations et compressions longitudinales ${$ les grandeurs acoustiques possibles étant les mêmes que celles d'un signal acoustique dans un liquide « normal »^[6] ou dans un gaz $}$ $($ voir ci-dessous à gauche $)$ ou,
transversal $($ onde $T)$ , exemple d'un signal acoustique $T$ dans le même acier où on voit une succession de cisaillements transversaux $($ voir ci-dessous à droite $)$ ,
Modèle:Transparentles grandeurs acoustiques possibles étant alors :
Modèle:Transparent $≻$ le « déplacement latéral $ζ$ des atomes » c.-à-d. leur déplacement transversal relativement à leur position au repos $($ ce déplacement est le même pour tous les atomes d'une même surface transversale, mais il diffère d'une surface transversale à une autre $)$ ou
Modèle:Transparent $≻$ la « contrainte de cisaillement $τ_{⊥}$ du matériau »^[8] définie par « $τ_{⊥} = \frac{F_{⊥}}{S}$ » où $F_{⊥}$ est la composante de force créant le déplacement latéral des atomes d'une surface transversale^[9] et $S$ l'aire de la surface sur laquelle s'exerce cette force.

Succession de dilatations et compressions à un instant $t$ dans un solide
Onde de cisaillement observée à un instant $t$ dans un solide

Célérité de propagation d'un signal acoustique

Modèle:AlLa « célérité de propagation du signal acoustique » notée « $c$ » est encore la « vitesse $($ non algébrisée $)$ de déplacement de la grandeur acoustique »,
Modèle:Transparentelle dépend de la masse volumique du milieu mais aussi de son élasticité ;
Modèle:Al Modèle:Transparent« $c$ est d'autant plus grande que la masse volumique et l'élasticité du milieu de propagation sont petites » ;
Modèle:Al Modèle:Transparentcomme la masse volumique d'un gaz est plus petite que celle d'un liquide^[10] laquelle est de même ordre de grandeur que celle d'un solide
Modèle:Al Modèle:Transparentalors que l'élasticité d'un gaz est plus grande que celle d'un liquide laquelle est plus grande que celle d'un solide,
Modèle:Al Modèle:Transparenton en déduit que :

la célérité de propagation d'une onde acoustique longitudinale dans un solide est plus grande que celle d'une onde acoustique de même nature dans un liquide « normal »^[6] $($ dans les conditions usuelles de température et de pression, elle vaut dans l'acier à $1 %$ de carbone $c_{long, acier} ≃$ $5900 m \cdot s^{- 1}$ et dans l'eau $c_{eau} ≃ 1500 m \cdot s^{- 1})$ ,
la célérité de propagation d'une onde acoustique dans un gaz $($ donc longitudinale $)$ est plus petite que celle d'une onde acoustique de même nature dans un liquide « normal »^[6]Modèle:,^[11] $($ dans les conditions usuelles de température et de pression, elle vaut dans l'eau $c_{eau} ≃ 1500 m \cdot s^{- 1}$ et dans l'air $c_{air} ≃ 340 m \cdot s^{- 1})$ .

Modèle:AlDans les solides $($ ou les liquides « très visqueux »^[7] $)$ la célérité d'un signal acoustique longitudinal est toujours plus grande que celle d'un signal acoustique transversal $($ dans les conditions usuelles de température et de pression elles valent dans l'acier à $1 %$ de carbone $c_{long, acier} ≃$ $5900 m \cdot s^{- 1}$ pour les ondes $L$ et $c_{transv, acier} ≃ 3200 m \cdot s^{- 1}$ pour les ondes $T)$ .

Grandeurs vibrantes en électricité, célérité de la propagation

Modèle:AlUn « signal électrique » est la « variation $($ de courte durée $)$ d'une grandeur électrique dans un milieu matériel conducteur de l'électricité » ^[12].

Notion d'intensité de courant et de tension

Modèle:AlCommentaire préliminaire : Ces notions seront vues plus en détail dans les paragraphes « notion de courant électrique et définition de l'intensité du courant en un point du circuit filiforme » et « potentiel d'un point d'un circuit électrique, choix de la référence de potentiel, définition de la tension entre deux points d'un circuit » du chap. $21$ de la leçon « Signaux physiques (PCSI) », seuls les éléments indispensables à la compréhension du paragraphe intitulé « grandeurs vibrantes en électricité, célérité de la propagation » sont introduits.

Notion de conducteur, isolant, semi-conducteur

Modèle:AlPour qu'un milieu soit conducteur il faut qu'il possède des éléments chargés mobiles que l'on appelle « porteurs de charge mobiles »^[13].

Modèle:AlUn milieu sera plus ou moins bon conducteur s'il y a suffisamment de porteurs de charge mobiles :

électrons de conduction pour un métal ^[14],
ions pour un électrolyte ^[15],
électrons de conduction $($ ou porteurs $n)$ et « trous » $($ ou porteurs $p)$ pour un semi-conducteur intrinsèque ^[16],
porteurs $n$ pour un semi-conducteur extrinsèque dopé $N$ ^[17] et
porteurs $p$ pour un semi-conducteur extrinsèque dopé $P$ ^[18].

Évaluation de la densité volumique particulaire des porteurs de charge mobiles dans quelques conducteurs typiques

Exemple du cuivre : il s'agit d'un conducteur métallique, les porteurs de charge mobiles sont donc les « électrons de conduction » ; en moyenne un électron de valence $($ le moins lié dans l'atome de cuivre $)$ étant libéré par atome de cuivre, on en déduit $N_{V, m} (élect de conduc) =$ $N_{V} (atomes de Cu)$ ;
Modèle:Transparent $≻$ données : densité du cuivre $d = 8, 95 = \frac{μ_{Cu}}{μ_{eau}}$ ^[19] d'où sa masse volumique $μ_{Cu} = 8950 k g \cdot m^{- 3}$ , masse molaire atomique du cuivre $M_{Cu} = 63, 5 g \cdot m o l^{- 1}$ et constante d'Avogadro^[20] $𝒩 = 6, 02 1 0^{23} m o l^{- 1}$ ;
Modèle:Transparent $≻$ on trouve $N_{V, m} ≃ N_{V} (atomes de Cu) = 𝒩 \frac{μ_{Cu}}{M_{Cu}} = 6, 02 1 0^{23} \times \frac{8950}{63, 5 1 0^{- 3}}$ soit finalement « $N_{V, m} ≃ 8, 5 1 0^{28} m^{- 3}$ ».
Exemple de solution aqueuse de chlorure de sodium : il s'agit d'un conducteur électrolytique, les porteurs de charge mobiles sont donc des « ions positifs $($ ou cations $)$ et négatifs $($ ou anions $)$ » ; le chlorure de sodium est un cristal ionique totalement dissocié dans l'eau selon « $N a C l_{s} \overset{eau}{⟶} N a_{aq}^{+} + C l_{aq}^{-}$ », les porteurs de charge mobile sont « les cations sodium hydratés $N a_{aq}^{+}$ » et « les anions chlorure hydratés $C l_{aq}^{-}$ », en même quantité $($ assurant l'électroneutralité de la solution $)$ ;
Modèle:Transparent $≻$ on considère une eau salée de concentration volumique molaire $c = 0, 1 m o l \cdot L^{- 1} = 1 0^{2} m o l \cdot m^{- 3}$ , on peut facilement évaluer $N_{V, m} (N a_{aq}^{+})$ $= N_{V, m} (C l_{aq}^{-})$ à partir de $c$ et de $𝒩$ selon « $N_{V, m} (N a_{aq}^{+}) = N_{V, m} (C l_{aq}^{-}) = 𝒩 c$ »,
Modèle:Transparent $≻$ on trouve alors $N_{V, m} (N a_{aq}^{+}) = N_{V, m} (C l_{aq}^{-}) =$ $6, 0 1 0^{23} \times 1 0^{2}$ en $m^{- 3}$ ^[21] soit « $N_{V, m} (N a_{aq}^{+}) = N_{V, m} (C l_{aq}^{-}) ≃ 6, 0 1 0^{25} m^{- 3}$ ».
Exemple de l'eau : elle est très légèrement ionisée selon « $2 H_{2} O \overset{eau}{⇄} H_{3} O_{aq}^{+} + H O_{aq}^{-}$ », les porteurs de charge mobiles sont « les cations oxonium hydratés $H_{3} O_{aq}^{+}$ »^[22] et « les anions hydroxydes hydratés $H O_{aq}^{-}$ », en même quantité dans l'eau pure $($ assurant l'électroneutralité de cette dernière $)$ ;
Modèle:Transparent $≻$ la densité volumique pour chaque porteur étant la même $N_{V, m} (H_{3} O_{aq}^{+}) = N_{V, m} (H O_{aq}^{-})$ , elle se détermine à partir de la valeur du $p H$ de l'eau pure à $25 °C$ , « $p H = 7, 0$ » d'où « une concentration volumique molaire en oxonium $[H_{3} O_{aq}^{+}] = 1 0^{- 7} m o l \cdot L^{- 1}$ » et « une densité volumique molaire du même ion $n_{V, m} (H_{3} O_{aq}^{+}) = 1 0^{- 4} m o l \cdot m^{- 3}$ »^[23] ;
Modèle:Transparent $≻$ en multipliant par $𝒩$ , on obtient la densité volumique particulaire commune des deux ions $N_{V, m} (H O_{aq}^{-}) =$ $N_{V, m} (H_{3} O_{aq}^{+}) = n_{V, m} (H_{3} O_{aq}^{+}) 𝒩 ≃ 1 0^{- 4} \times 6, 0 1 0^{23}$ soit finalement « $N_{V, m} (H_{3} O_{aq}^{+}) = N_{V, m} (H O_{aq}^{-}) ≃ 6, 0 1 0^{19} m^{- 3}$ » $($ d'où le qualificatif de « mauvais conducteur » $)$ .

Modélisation filiforme d'un conducteur, sens conventionnel du courant

Modèle:AlQuand une dimension $-$ longitudinale $-$ est très grande par rapport aux deux autres transversales, on modélise le conducteur par une portion dite « filiforme » correspondant à l'absence de dimensions transversales ;
Modèle:Alle sens du courant^[24] est, par définition, le sens de déplacement d'ensemble des porteurs de charge positive $($ et le sens contraire du déplacement d'ensemble des porteurs de charge négative $)$ ^[25].

Définition de l'intensité algébrique du courant

Modèle:AlPour algébriser l'intensité du courant, on définit $($ arbitrairement $)$ un sens $+$ de mesure de l'intensité du courant :

Modèle:All'intensité $($ algébrique $)$ « $i$ » du courant traversant le circuit filiforme en un point $M$ est « la charge traversant le point $M$ dans le sens $+$ par unité de temps » c.-à-d. par $s$ ou,

Modèle:Al Modèle:Transparentsi la charge $δ q$ traverse $M$ dans le sens $+$ pendant $δ t$ , « $i = \lim \limits_{δ t \to 0} \frac{δ q}{δ t}$ » ou,
Modèle:Al Modèle:Transparenten notant $d t$ l'infiniment petit représentant $δ t \to 0$ ^[26] et $d q$ l'infiniment petit correspondant à $δ q \to 0$ ^[27],
Modèle:Al Modèle:Transparent« $i = \frac{d q}{d t}$ s'exprimant en $A$ », $(1 A = 1 C \cdot s^{- 1})$ ;

Modèle:Alon représente le courant sur un circuit filiforme par une flèche sur les fils de connexion dans le sens $+$ de mesure de l'intensité algébrique et on indique celle-ci à côté de la flèche.

Nécessité d'imposer une tension aux bornes d'un récepteur pour qu'il soit traversé par un courant

Modèle:AlPour qu'il y ait circulation de courant dans la partie réceptrice d'un circuit filiforme, il faut que les porteurs soient soumis à une force motrice qui est d'origine électrique ; pour cela

Modèle:Al Modèle:Transparentle récepteur est relié à un générateur qui impose en tout point du récepteur un champ électrique $\vec{E} (M)$ , et par suite
Modèle:Al Modèle:Transparentun porteur de charge $q_{p}$ y subit une force électrique ${\vec{F}}_{élect} = q_{p} \vec{E}$ le mettant en mouvement dans le sens du courant si $q_{p} > 0$ et
Modèle:Al Modèle:Transparentdans le sens contraire si $q_{p} < 0$ ;
Modèle:Al Modèle:Transparenton en déduit que le courant dans un récepteur est toujours dans le sens du champ électrique $\vec{E}$ ;

Modèle:Alle porteur de charge $q_{p}$ dans le champ électrique $\vec{E}$ possède de l'énergie potentielle électrique $ℰ_{p, élec}$ ^[28] tout comme un objet ponctuel de masse $m$ dans le champ de pesanteur uniforme $\vec{g}$ possède de l'énergie potentielle de pesanteur $U_{pes}$ ;

Modèle:Al Modèle:Transparentdans l'hypothèse où $q_{p}$ est $> 0$ ^[29], son énergie potentielle électrique $ℰ_{p, élec} ↘$ dans le sens de $\vec{E}$ comme l'énergie potentielle de pesanteur de l'objet ponctuel $U_{pes} ↘$ dans le sens de $\vec{g}$ ${ℰ_{p, élec}$ est $\propto$ à $q_{p}$ comme $U_{pes}$ est $\propto$ à $m$ , l'autre facteur ne dépendant que de la position dans le champ $}$ ;

Modèle:Al Modèle:Transparenton définit l'énergie potentielle électrique du porteur de charge $q_{p} > 0$ ^[29] dans le champ électrique $\vec{E} (M)$ selon « $ℰ_{p, élec} =$ $q_{p} V (M)$ » où Modèle:Nobr représente le potentiel électrique en $M$ exprimé en $V$ » par analogie avec l'énergie potentielle de pesanteur d'un objet ponctuel de masse $m$ dans le champ de pesanteur $\vec{g}$ « $U_{pes} =$ $m g z$ »^[30] où « $z$ est l'altitude de l'objet par rapport au sol » ${$ le potentiel électrique en $M$ étant l'analogue de la grandeur $g z$ que l'on pourrait baptiser « potentiel de pesanteur en $M$ »^[31] $}$ ,

Modèle:Al Modèle:Transparentl'expression « $ℰ_{p, élec} = q_{p} V (M)$ avec $V (M)$ potentiel électrique en $M$ en $V$ » reste « applicable à un porteur de charge $q_{p} < 0$ »^[32] ;

Modèle:Al Modèle:Transparentle « potentiel électrique $V (M)$ en $M$ a la propriété de $↘$ dans le sens de $\vec{E}$ »^[33] ${$ comme le « potentiel de pesanteur en $M$ ^[31] Modèle:Nobr a la propriété de $↘$ dans le sens de $\vec{g}$ » $}$ ;

Modèle:Al Modèle:Transparentune énergie potentielle nécessitant de préciser sa référence^[34], il en est de même du potentiel électrique qui n'est donc défini qu'à une constante additive près, on choisit donc l'endroit où le potentiel est considéré comme nul et cet endroit définit la « masse » du circuit ^[35] ${$ analogue de l'origine des altitudes pour le « potentiel de pesanteur »^[31] $}$ ;

Modèle:Al Modèle:Transparenton peut donc affirmer que le courant dans un récepteur est toujours dans le sens décroissant des potentiels.

Modèle:AlDe même que l'on définit une dénivellation dans un champ de pesanteur comme une différence d'altitudes,
Modèle:Al Modèle:Transparenton définit une tension dans un champ électrique comme une différence de potentiels ou d.d.p., plus précisément
Modèle:Al Modèle:Transparentla tension $u_{A B} = V (A) - V (B)$ représentée sur le schéma d'un circuit par une flèche à côté du circuit allant de $B$ vers $A$ , sa valeur notée à côté de la flèche ;

Modèle:Alsi le courant dans un récepteur circule de

A

vers

B

, les potentiels des extrémités sont donc tels que

V (A) > V (B)

\Rightarrow

la tension

u_{A B}

est

> 0

,
Modèle:Al Modèle:Transparentla tension

u_{A B}

étant représentée par une flèche à côté du circuit allant de

B

vers

A

et le courant par une flèche sur le circuit allant de

A

vers

B

, nous en déduisons que

« la flèche tension aux bornes d'un récepteur est toujours de sens contraire à la flèche courant circulant dans le récepteur »
pourvu que les flèches tension et courant définissent des tensions et des intensités toutes deux positives.

Tension aux bornes d'un générateur et sens du courant dans ce dernier

Modèle:AlLe générateur, vis-à-vis des porteurs de charge mobiles, joue le rôle du « tire-fesses » pour des skieurs ou de « pompe » pour l'eau qui doit monter aux étages,
Modèle:Al Modèle:Transparentl'énergie potentielle électrique des porteurs de charge mobiles arrivant par la borne « $-$ » d'un générateur de tension permanente^[36]Modèle:,^[37] ou
Modèle:Al Modèle:Transparentpar la borne noire d'un générateur de fonctions^[38]
Modèle:Al Modèle:Transparentdoit croître pour que ces porteurs atteignent l'autre borne ${$ à savoir la borne Modèle:Nobr d'un générateur de tension permanente^[39] ou la borne rouge d'un générateur de fonctions^[40] $}$ ,
Modèle:Al Modèle:Transparentla croissance de l'énergie potentielle électrique des porteurs de charge mobiles lors de la traversée d'un générateur dans le sens du courant que ce dernier délivre correspond à « une force électrique s'exerçant sur un porteur ${\vec{F}}_{élect} = q_{p} \vec{E}$ résistive » tout comme la composante résistive du poids du skieur le long de la pente quand ce dernier remonte en « tire-fesses » ou comme le poids résistif de l'eau quand celle-ci est montée aux étages à l'aide d'une pompe ;

Modèle:Al Modèle:Transparentpour que ceci soit possible il faut donc que les porteurs de charge mobiles lors de la traversée d'un générateur dans le sens du courant que ce dernier délivre subissent une force motrice, cette dernière ayant une origine qui dépend de la nature du générateur $($ « origine électrochimique » pour une pile avec introduction de « phénomènes d'oxydo-réduction » ou « origine électromécanique » pour un alternateur avec introduction de « phénomènes d'induction » $)$ peut être écrite en fonction d'un « champ dit électromoteur » noté « ${\vec{E}}_{électromot} (M)$ » indépendant du porteur, « ${\vec{F}}_{électromot} = q_{p} {\vec{E}}_{électromot}$ »^[41] ; cette force due au champ électromoteur étant la cause de la mise en mouvement des porteurs de charge mobiles dans le générateur est dans le sens du courant si $q_{p}$ est $> 0$ $($ et dans le sens contraire si $q_{p}$ est $< 0)$ d'où la conclusion sur le sens du champ électromoteur dans le générateur et celui du courant délivré par ce dernier ;

Modèle:Al Modèle:Transparentle courant délivré par un générateur est toujours $($ à l'intérieur de ce dernier $)$ dans le sens du champ électromoteur ${\vec{E}}_{électromot}$ c.-à-d.
Modèle:Al Modèle:Transparentdans le sens contraire du champ électrique $\vec{E}$ ;

Modèle:Alle lien entre champ électrique et potentiel restant le même que dans un récepteur à savoir « le champ électrique est dans le sens des potentiels $↘$ », nous en déduisons que
Modèle:Al Modèle:Transparentle courant délivré par un générateur est toujours $($ à l'intérieur de ce dernier $)$ dans le sens croissant des potentiels.

Modèle:AlDéfinissant toujours une tension

u_{A B}

comme la différence de potentiels

V_{A} - V_{B}

et la représentant par une flèche à côté du générateur allant de

B

vers

A

, la valeur de la tension notée à côté de la flèche, nous pouvons affirmer que

la flèche tension aux bornes d'un générateur est toujours de même sens que la flèche courant circulant dans ce dernier

(

pourvu que les flèches tension et courant définissent des tensions et des intensités toutes deux positives^[42]

)

.

Les deux principales grandeurs vibrantes en électricité

Modèle:AlNous savons déjà qu'un signal électrique est la variation $($ de courte durée $)$ d'une grandeur électrique qui peut être une tension ou une intensité de courant :

Modèle:Alexemple : dans un câble coaxial, on crée un signal électrique de grandeur vibrante « tension » ou « intensité de courant » à une extrémité $S$ du câble $($ reliée à un générateur $)$ pour l'envoyer à l'autre extrémité $R$ $($ reliée à un récepteur $)$ , dans la section $M$ du câble on retrouve les grandeurs vibrantes « tension » ou « intensité de courant » ;

Modèle:Al Modèle:Transparentle signal associé à la grandeur vibrante « tension » $u_{M T} = V (M) - V (T)$ est transversal^[43] et
Modèle:Al Modèle:Transparentcelui associé à la grandeur vibrante « intensité du courant » $i_{S \to R} (M)$ est longitudinal^[44].

Célérité de propagation d'un signal électrique

Modèle:AlLa « célérité de propagation du signal électrique, notée $c$ », est la « vitesse $($ non algébrisée $)$ de déplacement de la grandeur électrique », elle dépend de la nature du diélectrique ^[45] séparant les deux conducteurs de la ligne, « sa valeur maximale est $c ≃ 300 000 k m \cdot s^{- 1}$ »^[46].

Modèle:AlRemarque : Parmi les différentes vitesses intervenant dans un signal électrique se propageant le long d'un câble coaxial, il convient de distinguer :
Modèle:Al Modèle:Transparent $≻$ « la célérité de la propagation » correspondant à la rapidité de transmission de l'information de valeur maximale $300 000 k m \cdot s^{- 1}$ , de
Modèle:Al Modèle:Transparent $≻$ « la vitesse d'agitation thermique des porteurs de charge mobiles » d'ordre de grandeur $100 m \cdot s^{- 1}$ à température ordinaire pour des électrons de conduction et de
Modèle:Al Modèle:Transparent $≻$ « la vitesse moyenne de ces porteurs de charge mobiles correspondant à une intensité donnée », vitesse qui dépend de la valeur de l'intensité mais qui reste, pour des intensités usuelles, inférieure à $1 m m \cdot s^{- 1}$ .

Grandeurs vibrantes en électromagnétisme, célérité de la propagation

Modèle:AlUn signal électromagnétique est la variation $($ de courte durée $)$ d'un champ électromagnétique^[47].

Notion de champ électromagnétique

Modèle:AlUn ensemble de charges ponctuelles $($ im $)$ mobiles crée, en son voisinage, un « champ électrique » $\vec{E} (M)$ ^[48] et
Modèle:Transparentsi les charges ponctuelles de l'ensemble sont mobiles, ce dernier crée, en son voisinage, en plus du champ électrique $\vec{E} (M)$ , un « champ magnétique » $\vec{B} (M)$ ^[49].

Modèle:AlRemarque : dans le cas où des charges ponctuelles sont immobiles dans un 1^er référentiel d'étude, ces dernières créent un champ électrique sans champ magnétique mais si on considère un 2^ème référentiel d'étude en mouvement par rapport au 1^er, les charges ponctuelles y devenant mobiles créent un champ magnétique en plus d'un champ électrique ;
Modèle:Al Modèle:Transparentsuivant le référentiel d'étude considéré, un ensemble de charges ponctuelles est source d'un couple de champs électrique et magnétique $($ avec, pour certains référentiels, un des deux champs Modèle:Nobr ce couple définissant un « champ électromagnétique » ${\vec{E} (M); \vec{B} (M)}$ ^[50].

Milieu de propagation et grandeur vibrante

Modèle:AlUn signal électromagnétique n'a pas besoin de milieu matériel pour se propager, il traverse, par exemple, l'espace « vide » entre une galaxie lointaine et la Terre
Modèle:Al Modèle:Transparentsous la forme d'un signal optique visible ou invisible,
Modèle:Al Modèle:Transparentd'un signal hertzien $($ ou radio $)$ ,
Modèle:Al Modèle:Transparentde rayons $X$ ou de rayons $γ$ ;

Modèle:Al Modèle:Transparenttoutefois il peut traverser un milieu matériel, par exemple il peut être « guidé le long d'un câble de transmission constitué de deux conducteurs » $($ dans ce cas le signal électromagnétique est la cause du signal électrique introduit au paragraphe « les deux principales grandeurs vibrantes en électricité » plus haut dans ce chapitre $)$ ;
Modèle:Al Modèle:Transparentautre exemple un signal optique $($ cas particulier de signal électromagnétique $)$ peut traverser des milieux matériels comme l'air, l'eau ou le verre, ces milieux sont alors qualifiés de « transparents » $($ les milieux ne permettant pas aux signaux optiques de traverser étant qualifiés d'« opaques » $)$ ;

Modèle:Alla grandeur vibrante est le « champ électromagnétique » constitué de ses deux composantes vectorielles « électrique et magnétique » ;

Modèle:Al« dans le vide le signal électromagnétique est nécessairement transversal^[51] » mais
Modèle:Al« dans la matière, à la composante transversale peut s'y ajouter une composante longitudinale ».

Célérité de propagation d'un signal électromagnétique

Modèle:AlLa « célérité de propagation du signal électromagnétique » est la « vitesse $($ non algébrisée $)$ de déplacement du champ électromagnétique »,
Modèle:Al Modèle:Transparentdans le vide, elle est notée $c$ et vaut « $c ≃ 300 000 k m \cdot s^{- 1}$ » et
Modèle:Al Modèle:Transparentdans un milieu matériel, elle est notée $v$ en vérifiant toujours « $v < c ≃ 300 000 k m \cdot s^{- 1}$ » $($ la valeur de $v$ dépendant de la nature du milieu traversé $)$ .

Limitation de l'étude aux grandeurs vibrantes périodiques

Modèle:AlPour la suite nous envisageons une grandeur vibrante « source » ^[52] « $T - périodique$ », de fréquence $f = \frac{1}{T}$ ^[53],
Modèle:Al Modèle:Transparentcette grandeur vibrante définit le « signal physique » transporté par l'« onde » ^[54], il est donc « $T - périodique$ » a priori « non sinusoïdal $($ ou non harmonique $)$ ».

Exemple de signal périodique sinusoïdal

L'onde correspondant au signal physique transporté est également dite « périodique sinusoïdale ».

Modèle:AlSi on note «

s (t)

le signal

T - périodique

source » ^[55], celui-ci est sinusoïdal s'il s'écrit sous la forme

«

s (t) = A \cos (2 π f t + φ) = A \cos (2 π \frac{t}{T} + φ) = A \cos (ω t + φ)

»

où «

ω = 2 π f = \frac{2 π}{T}

»^[56] est la « pulsation du signal source » sinusoïdal,

A

étant l'« amplitude » et

φ

la « phase à l'origine des temps

(

ou initiale

)

»,

ω t + φ

étant la « phase à l'instant

t;

».

Analyse spectrale d'un signal périodique

Modèle:AlFaire l'analyse spectrale d'un « signal » périodique de fréquence $f$ , c'est réaliser son développement en série de Fourier^[57] ;
Modèle:Al Modèle:Transparentà tout « signal » périodique $s (t)$ on associe l'éventuelle composante continue $C_{0}$ et les couples ${C_{n}, φ_{n}}$ d'amplitude et de phase initiale de l'harmonique de rang $n$ .

Modèle:Définition Modèle:Définition Modèle:Remarque

Exemple d'un signal créneau symétrique

Modèle:AlCi-dessous à gauche le tracé du graphe d'un signal créneau^[58] « symétrique »^[59] « impair »^[60] d'amplitude $1 V$ et de fréquence $1 k H z$ $($ donc de période $1 m s)$ :

Tracé d'un signal créneau^[58] « symétrique »^[59] sur un intervalle large d'une période $($ fréquence $1 k H z)$
Spectre des $20$ premiers harmoniques d'un signal créneau^[58] « symétrique »^[59] $($ fréquence $1 k H z)$

Modèle:AlCi-dessus à droite le spectre d'amplitudes^[61] d'un signal créneau^[58] « symétrique »^[59] pour les $20$ premiers harmoniques ;
Modèle:Al Modèle:Transparentla décroissance de l'amplitude des harmoniques avec leur rang se fait lentement car $\propto$ à $\frac{1}{n}$ .

Modèle:Proposition Modèle:Proposition Modèle:Preuve

Exemple d'un signal triangulaire symétrique

Modèle:AlCi-dessous à gauche le tracé du graphe d'un signal triangulaire « symétrique »^[59] « impair »^[60] d'amplitude $1 V$ et de fréquence $1 k H z$ $($ donc de période $1 m s)$ :

Tracé d'un signal triangulaire « symétrique »^[59] sur un intervalle large d'une période $($ fréquence $1 k H z)$
Spectre des $20$ premiers harmoniques d'un signal triangulaire « symétrique »^[59] $($ fréquence $1 k H z)$

Modèle:AlCi-dessus à droite le spectre d'amplitudes^[61] d'un signal triangulaire « symétrique »^[59] pour les $20$ premiers harmoniques ;
Modèle:Al Modèle:Transparentla décroissance de l'amplitude des harmoniques avec leur rang se fait assez rapidement car $\propto$ à $\frac{1}{n^{2}}$ .

Modèle:Proposition Modèle:Proposition Modèle:Preuve

Notion de filtrage linéaire et réponse fréquentielle du filtre à un signal périodique

Notion de filtre linéaire

Modèle:AlUn filtre est dit linéaire quand, d'un « signal d'entrée sinusoïdal » il donne un « signal de sortie sinusoïdal de même fréquence » ;
Modèle:Al Modèle:Transparentce « signal de sortie » est appelé « réponse du filtre au signal d'entrée »,
Modèle:Al Modèle:Transparentson amplitude et sa phase initiale dépendent de l'amplitude et la phase initiale du « signal d'entrée »
Modèle:Al Modèle:Transparentmais aussi de « sa fréquence »^[62] ;

Modèle:Alde plus pour que le filtre soit linéaire il faut que « la réponse du filtre à une somme de signaux d'entrée » soit « la somme des réponses du filtre à chaque signal d'entrée pris isolément »^[63].

Réponse fréquentielle du filtre (linéaire) à un signal d'entrée périodique

Modèle:Définition

Synthèse spectrale (de Fourier) permettant de trouver le signal périodique à partir de sa représentation fréquentielle

Modèle:AlIl s'agit de « trouver le signal de sortie $s_{s} (t)$ connaissant sa représentation fréquentielle $C_{0, s}, {C_{n, s}, φ_{n, s}}_{(n \in ℕ^{*})}$ » ;
Modèle:Al Modèle:Transparentce signal de sortie $s_{s} (t)$ est la « somme infinie $C_{0, s} + \sum_{n = 1}^{\infty} C_{n, s} \cos (2 π n f t + φ_{n, s})$ », faire cela pratiquement c'est réaliser une « synthèse $($ spectrale $)$ de Fourier »^[64].

Modèle:AlRemarque : Le signal de sortie étant une somme $($ théoriquement infinie $)$ d'harmoniques de fréquences multiples d'une même fréquence $f$ $\Rightarrow$ c'est un « signal périodique de fréquence $f$ »^[65].

Filtre passe-bas idéal

Modèle:AlIntroduit pour son utilisation dans les paragraphes « nombre minimal de 1^ers harmoniques nécessaire pour reconstruire un signal triangulaire symétrique » et « nombre minimal de 1^ers harmoniques nécessaire pour reconstruire un signal créneau symétrique » plus loin dans ce chapitre ;

Modèle:AlDescription d'un filtre passe-bas idéal : c'est un filtre idéal laissant passer, sans aucune modification, les fréquences inférieures à une fréquence critique $($ appelée fréquence de coupure $)$ et
Modèle:Al Modèle:Transparentarrêtant toutes les fréquences supérieures à cette fréquence critique ;

Modèle:Al Modèle:Transparentla fréquence de coupure du filtre passe-bas idéal ${$ utilisé dans les paragraphes « nombre minimal de 1^ers harmoniques nécessaire pour reconstruire un signal triangulaire symétrique » et « nombre minimal de 1^ers harmoniques nécessaire pour reconstruire un signal créneau symétrique » plus loin dans ce chapitre $}$
Modèle:Al Modèle:Transparentest celle de l'harmonique de rang $10$ des signaux d'entrée, c.-à-d. que le filtre laisse passer tous les harmoniques jusqu'au rang $10$ inclus.

Nombre minimal de premiers harmoniques nécessaire pour reconstruire un signal triangulaire symétrique

Modèle:AlL'utilisation des $10$ 1^ers harmoniques donne un signal triangulaire de « qualité » $($ seules les pointes correspondant aux sommets du signal triangulaire ne sont pas reproduits $)$ ;

Modèle:Alon conçoit bien qu'utiliser les harmoniques jusqu'au « rang $3$ , voire $5$ ^[66] »^[67] devrait suffire.

Modèle:Remarque Modèle:Clr

Nombre minimal de premiers harmoniques nécessaire pour reconstruire un signal créneau symétrique

Modèle:AlL'utilisation des $10$ 1^ers harmoniques donne un signal créneau^[58] de « qualité très médiocre » $($ fluctuations importantes sur les plateaux de crête et passage d'un plateau de crête à l'autre non instantané $)$ ;

Modèle:Alon conçoit bien qu'utiliser les harmoniques jusqu'au « rang $30$ , voire $50$ ^[66] »^[68] semble nécessaire.

Modèle:Remarque

Ordre de grandeur des fréquences dans les domaines acoustique et électromagnétique

Domaine acoustique

Modèle:AlSons audibles par un être humain entre $20$ et $20 000 H z$ $($ graves pour les B.F.^[69] et aigus pour les H.F.^[70] $)$ ref> La fréquence du $L a 3$ : $440 H z$ .</ref> ;

Modèle:Al Modèle:Transparenten deçà de $20 H z$ , se situent les infrasons $($ nous n'entendons pas les sons en dessous de $20 H z$ mais nous pouvons partiellement les ressentir avec notre corps, en particulier avec notre cage thoracique ; la 1^ère moitié de la 1^ère octave ^[71] perçue par l'humain $[20 H z; 40 H z]$ est à la frontière entre l'infrason et le grave, elle produit une impression, à la fois auditive et physique, qui donne une sensation de « poids » ; les tremblements de terre, éruptions volcaniques, tonnerre et d'autres phénomènes naturels produisent des infrasons à un niveau parfois extrêmement élevé ; d'autre part des études récentes ont montré que les infrasons jouent un rôle dans la communication chez certains mammifères tels que les éléphants, les girafes ou les baleines $)$ et

Modèle:Al Modèle:Transparentau-delà de $20 000 H z$ , se situent les ultrasons $($ de nombreux animaux, comme les chiens ou les chauve-souris, peuvent entendre les ultrasons, certains peuvent en émettre : les chauve-souris émettent des ultrasons qui se répercutent sur les objets environnants, ce qui leur permet ainsi de percevoir leur environnement, il s'agit du phénomène d'« écholocation » $)$ .

Domaine électromagnétique

Modèle:AlOn distingue quatre grands domaines suivant les valeurs de fréquence :

Ondes lumineuses

Modèle:AlLumières visibles par un être humain entre $4 1 0^{14}$ et $8 1 0^{14} H z$ ${$ côté de la plus B.F.^[69] « rouge » et de la plus H.F.^[70] « violet » $}$ ;

Modèle:Al Modèle:Transparenten deçà de $4 1 0^{14} H z$ se trouve l'infrarouge qui s'étend approximativement jusqu'à $3 1 0^{11} H z$ ${$ l'infrarouge est associé à la chaleur car, à température ambiante, les objets émettent spontanément des radiations dans le domaine infrarouge $}$ et

Modèle:Al Modèle:Transparentau-delà de $8 1 0^{14} H z$ se trouve l'ultraviolet qui s'étend approximativement jusqu'à $3 1 0^{16} H z$ ${$ en faible quantité, le rayonnement UV^[72] est bénéfique et est indispensable à la synthèse de vitamine $D$ ; les UV^[72] servent également à traiter plusieurs maladies, dont le rachitisme, le psoriasis, l'eczéma ; en plus hautes quantités, lors d'expositions prolongées au soleil ou à des rayonnements artificiels $($ issus par exemple de lampes ou de dispositifs industriels type poste à souder $)$ , ils peuvent provoquer des cancers cutanés ou oculaires, un vieillissement prématuré de la peau, ainsi que des cataractes $}$ .

Ondes hertziennes (ou radioélectriques)

Modèle:AlPour les ondes radio réglementées les fréquences sont entre $9 1 0^{3}$ et $3 1 0^{11} H z$ ^[73] soit entre $9 k H z$ et $300 G H z$ ;

entre $3$ et $30 k H z$ ce sont des ondes myriamétriques $($ communication avec les sous-marins, implants médicaux $\dots)$ ,
entre $30$ et $300 k H z$ des grandes ondes ou ondes longues $($ radionavigation, radiodiffusion G.O.^[74] $\dots)$ ,
entre $300 k H z$ et $3 M H z$ des petites ondes ou ondes moyennes $($ radio AM^[75], service maritime, appareil de recherche de victimes d'avalanche $)$ ,
entre $3$ et $30 M H z$ des ondes courtes $($ militaire, radiodiffusion, aéronautique, météo $\dots)$ ,
entre $30$ et $300 M H z$ des ondes ultra-courtes $($ radio FM^[76], gendarmerie nationale, pompiers $\dots)$ ,
entre $300 M H z$ et $3 G H z$ des ondes décimétriques $($ G.P.S.^[77] ou assistant de navigation, Wi-Fi^[78], télévision $\dots)$ ,
entre $3$ et $30 G H z$ des ondes centimétriques $($ micro-ondes, radar météorologique $\dots)$ ,
entre $30$ et $300 G H z$ des ondes millimétriques $($ liaison vidéo transportable $\dots)$ .

Rayons X

Modèle:AlEntre $3 1 0^{16}$ et $3 1 0^{19} H z$ $($ ou entre $30 P H z$ et $30 E H z$ ^[79] $)$ , les rayons X sont un rayonnement ionisant utilisé dans de nombreuses applications dont l'imagerie médicale par radiographie standard et la cristallographie.

Rayonnements gamma

Modèle:AlAu-delà de $3 1 0^{19} H z$ $($ c.-à-d. au-delà de $30 E H z$ ^[79] $)$ , les ondes sont nommés « rayonnements gamma » $($ noté $γ)$ , ils sont produits par la désexcitation d'un noyau atomique résultant d'une désintégration $($ processus d'émission appelé radioactivité $γ)$ ^[80] ;

Modèle:Alles rayonnements gamma provenant de retombées radioactives seraient probablement le plus grand danger dans le cas d'une guerre nucléaire ; si les rayonnements γ sont moins ionisants que les rayons α ou les rayons β, ils demandent des épaisseurs de blindage beaucoup plus importantes pour s'en protéger $($ de l'ordre de quelques mètres d'épaisseur de béton armé $)$ ; ils peuvent produire des dégâts similaires à ceux produits par les rayons X et les autres rayonnements ionisants tels que brûlures, cancers et mutations génétiques.

Notes et références

↑ ^1,0 et ^1,1 c.-à-d. liquide ou gazeux.
↑ Et aussi les liquides très visqueux.
↑ $\vec{n}$ est un vecteur unitaire $⊥$ à $S$ , dirigé vers l'intérieur de l'objet.
↑ $\vec{τ}$ est un vecteur unitaire tangentiel à $S$ , choisi dans le plan contenant $\vec{F}$ et $\vec{n}$ .
↑ La pression atmosphérique dans les conditions usuelles d'altitude et de température étant au voisinage de $1 0^{5} P a$ , on utilise une unité dérivée « le bar » dont la conversion est $1 b a r = 1 0^{5} P a$ .
↑ ^6,0 ^6,1 ^6,2 et ^6,3 Dans cette catégorie on exclut les liquides très visqueux pour lesquels on observe aussi un signal transversal.
↑ ^7,0 et ^7,1 La très grande viscosité dans un liquide fait que ce dernier a un comportement plus proche de celui d'un solide que de celui d'un liquide « normal » $($ revoir la note « ⁷ » plus haut dans ce chapitre justifiant le qualificatif « normal » $)$ .
↑ De même homogénéité qu'une surpression, s'exprimant en $P a$ et le plus souvent en un multiple le $M P a = 1 0^{6} P a = 10 b a r$ .
↑ Dans une même surface transversale $𝒮$ , si la surface transversale de droite $𝒮_{d}$ est décalée vers le haut par rapport à la surface $𝒮$ considérée, $𝒮_{d}$ exerce une force vers le haut sur $𝒮$ de composante $F_{⊥}$ et si la surface transversale de gauche $𝒮_{g}$ est décalée vers le bas par rapport à la surface $𝒮$ considérée, $𝒮_{g}$ exerce une force vers le bas sur $𝒮$ de composante $- F_{⊥}$ .
↑ Un gaz a une masse volumique plus faible qu'un liquide dans les mêmes conditions de température et de pression, approximativement d'un facteur $1000$ .
↑ La densité et l'élasticité ont des effets contraires sur la célérité, l'augmentation de la densité a pour effet de diminuer la célérité de propagation alors que la diminution de l'élasticité pour effet d'augmenter cette célérité, les liquides étant plus denses mais moins élastiques que les gaz, on remarque donc que l'effet de l'élasticité est prépondérant.
↑ La grandeur électrique peut être une tension ou une intensité de courant ; sa variation peut être constatée par rapport à son absence $($ de tension ou d'intensité $)$ ou par rapport à une tension ou intensité permanente, cette dernière constituant la valeur dite de « repos » ou de « polarisation ».
↑ Les éléments chargés fixes comme il peut en exister dans les milieux non fluides $($ c.-à-d. solides $)$ ne jouant aucun rôle dans la conduction.
↑ La densité volumique particulaire a pour ordre de grandeur $N_{V, m} ≃ 1 0^{28} m^{- 3}$ , calcul exposé ci-après dans le cas du cuivre.
↑ La densité volumique particulaire dépend de la concentration de la solution mais usuellement elle ne dépasse pas $N_{V, m} ≃ 1 0^{25} m^{- 3}$ , calcul exposé dans le cas d'une solution décimolaire de chlorure de sodium et dans le cas de l'eau pure $($ très mauvais conducteur $)$ .
↑ Un semi-conducteur intrinsèque est un semi-conducteur pur $($ par exemple du silicium $S i)$ , il est isolant à basse température $($ un isolant ayant une densité volumique particulaire $≲ 1 0^{7} m^{- 3})$ et mauvais conducteur à température ordinaire $($ seuls quelques électrons de valence ont suffisamment d'énergie pour devenir des électrons de conduction, ils laissent alors derrière eux un site de valence vide et un électron de valence des atomes voisins peut venir l'occuper laissant à son tour derrière lui son site initial de valence vide $)$ ;
Modèle:Alpour simplifier l'étude $($ pour qu'il n'y ait pas deux types de porteurs de charge négative mobiles « les électrons de conduction » et « les électrons de valence sautant d'un site occupé à un site vide » $)$ les électroniciens considèrent qu'aucun électron de valence ne peut migrer, les sites de valence restant tous occupés $($ pour les sites réellement vides, conséquence d'un électron de valence devenu électron de conduction, l'électron de conduction restant mobile ils ajoutent fictivement un électron de valence sans possibilité de migrer et ils y superposent une particule fictive mobile de charge positive qu'ils appellent « trou » $)$ du point de vue électrique ils ajoutent donc fictivement une charge nulle $($ avec la propriété suivante : la superposition d'un « trou » et d'un « électron de valence » est équivalente à un site vide $)$ ;
Modèle:Alils remplacent alors la migration d'un électron de valence d'un site occupé $(1)$ à un site vide $(2)$ par la migration d'un trou du site $(2)$ au site $(1)$ , le départ du trou du site $(2)$ découvrant l'électron de valence et le rendant réel alors que l'arrivée du trou sur le site $(1)$ couvrant l'électron de valence et rendant ce dernier fictif, la superposition étant équivalente à un site vide ;
Modèle:Alil y a donc deux types de porteurs de charge mobiles : les « électrons de conduction » et les « trous » en quantités égales.
Modèle:AlLa densité volumique particulaire à température ordinaire est nettement plus faible que dans un métal $N_{V, m} ≃ 1 0^{16} m^{- 3}$ et elle est quasi-nulle à basse température.
↑ Un semi-conducteur extrinsèque dopé $N$ est un semi-conducteur $($ par exemple $S i)$ dans lequel on a ajouté des impuretés pentavalentes $($ par exemple d'arsenic $A s)$ ${$ on rappelle la définition de la valence d'un élément : nombre d'électrons de valence qui peuvent être cédés ou captés pour que la couche de valence devienne vide ou complètement remplie $}$ l'électron supplémentaire par rapport au semi-conducteur tétravalent pouvant relativement aisément se déplacer, il constitue le porteur de charge mobile, la densité volumique particulaire ayant pour ordre de grandeur $N_{V, m} ≃ 1 0^{22} m^{- 3}$ ${$ on peut ainsi négliger la semi-conduction intrinsèque $}$ .
↑ Un semi-conducteur extrinsèque dopé $P$ est un semi-conducteur $($ par exemple $S i)$ dans lequel on a ajouté des impuretés trivalentes $($ par exemple de gallium $G a)$ , le site de l'électron « manquant » par rapport au semi-conducteur tétravalent est remplacé par la présence simultanée d'un électron de valence fictif et d'un trou fictif, et comme dans un semi-conducteur intrinsèque les électrons de valence ajoutés restent fixes et les trous peuvent se déplacer pour « recouvrir » d'autres électrons de valence, les trous constituant donc les porteurs de charge mobiles, la densité volumique particulaire ayant le même ordre de grandeur que dans les semi-conducteurs dopés $N$ , $N_{V, m} ≃$ $1 0^{22} m^{- 3}$ ${$ on peut ainsi négliger la semi-conduction intrinsèque $}$ .
↑ La masse volumique de l'eau vaut $μ_{eau} = 1000 k g \cdot m^{- 3}$ .
↑ Lorenzo Romano Amedeo Carlo Avogadro (1776 - 1856) est un physicien et chimiste du Piémont $($ région actuelle de l'Italie $)$ à qui on doit essentiellement la loi d'Avogadro Ampère qu'il énonça en $1811$ et proposée indépendamment par Ampère en $1814$ , celle-ci spécifiant que « des volumes égaux de gaz parfaits différents, aux mêmes conditions de température et de pression, contiennent le même nombre de molécules ».
Modèle:AlAndré-Marie Ampère (1775 - 1836), mathématicien, physicien, chimiste et philosophe français, peut être considéré comme l'un des premiers artisans de la mathématisation de la physique, il a édifié les fondements théoriques de l'électromagnétisme et a découvert les bases de l'électronique de la matière.
↑ En physique l'unité de volume du S.I. $($ Système international $)$ est le $m^{3}$ et non le $L$ .
↑ L'ion oxonium est encore appelé ion hydronium.
↑ Il s'agit en fait de la même grandeur mais la première est utilisée en chimie et la seconde en physique $($ pour souligner la différence d'utilisation nous adoptons des noms différents ainsi que des notations différentes $)$ ; de plus les unités employées ne sont pas les mêmes ${$ on rappelle que l'unité de volume dans le S.I. $($ Système international $)$ est le $m^{3}$ et non le $L}$ .
↑ Ce sens est qualifié de « conventionnel » car, dans la plupart des matériaux conduisant plus ou moins l'électricité, il y a deux types de porteurs de charge mobiles circulant en sens inverse $($ quand un mouvement d'ensemble est imposé $)$ , il y avait donc deux choix possibles ; c'est en $1820$ que le français Ampère définit la grandeur « courant » matérialisée par la circulation des deux types de porteurs de charge mobiles en définissant, par convention, le sens du courant comme le sens de circulation de l'un des types de porteurs de charge mobiles, les porteurs de charge mobiles de signe opposé correspondant au sens contraire du courant $\dots$ mais le choix aurait pu être l'inverse, il s'agit donc d'un choix historique ;
Modèle:AlAndré-Marie Ampère (1775 - 1836), mathématicien, physicien, chimiste et philosophe français, peut être considéré comme l'un des 1^ers artisans de la mathématisation de la physique, il a édifié les fondements théoriques de l'électromagnétisme et a découvert les bases de l'électronique de la matière.
↑ Pour qu'il y ait déplacement d'ensemble de porteurs de charge mobiles il faut que le conducteur soit branché dans un circuit dans lequel il y a au moins un générateur qui lui impose une tension entre ses bornes $($ cette notion de tension est vue ultérieurement dans les paragraphes « nécessité d'imposer une tension aux bornes d'un récepteur pour qu'il soit traversé par un courant » et « tension aux bornes d'un générateur et sens du courant dans ce dernier » plus loin dans ce chapitre $)$ .
↑ $d t$ est appelée « durée élémentaire » et correspond à l'élément différentiel de temps, voir le paragraphe « élément différentiel d'une variable » du chap. $4$ de la leçon « Outils mathématiques pour la physique (PCSI) ».
↑ $d q$ correspond à l'élément différentiel de charge, voir le paragraphe « élément différentiel d'une variable » du chap. $4$ de la leçon « Outils mathématiques pour la physique (PCSI) » ;
Modèle:Alen fait à l'échelle microscopique, la charge n'est pas une grandeur continue mais quantifiée, elle est toujours un multiple de la charge élémentaire $e ≃ 1, 6 1 0^{- 19} C$ , mais à l'échelle macroscopique ${$ ou mésoscopique $($ un échantillon est d'échelle mésoscopique s'il est de dimensions infiniment petites à l'échelle macroscopique mais infiniment grandes à l'échelle Modèle:Nobr toute charge comprenant un grande nombre de charges élémentaires $\Rightarrow$ chaque charge élémentaire peut être considérée comme quasi-nulle ce qui revient à envisager le caractère continu de la charge.
↑ Les énergies potentielles seront notées $U$ sauf quand il y a risque de confusion, ce qui est le cas en électricité, $U$ étant réservée à la tension.
↑ ^29,0 et ^29,1 On se limite au choix de $q_{p} > 0$ car on souhaite d'induire une formule pour l'énergie potentielle électrique de la charge $q_{p}$ dans le champ électrique $\vec{E}$ par analogie avec celle d'un objet ponctuel de masse $m$ $($ nécessairement $> 0)$ dans le champ de pesanteur $\vec{g}$ .
↑ Avec cette formule, l'énergie potentielle étant choisie nulle au niveau du sol, on dit que sa référence est le sol.
↑ ^31,0 ^31,1 et ^31,2 Mais cette notion de « potentiel de pesanteur au point $M$ » n'est quasiment jamais introduite $($ de plus il s'agit d'une appellation personnelle $)$ .
↑ En un point $M$ de potentiel $V (M)$ , un porteur de charge $q_{p} < 0$ ayant une énergie potentielle électrique opposée à celle d'un porteur de charge ${q^{'}}_{p} = | q_{p} | > 0$ , la décroissance de l'énergie potentielle électrique du porteur de charge $q_{p} < 0$ se fait dans le sens $↗$ des potentiels électriques alors que celle de l'énergie potentielle électrique du porteur de charge ${q^{'}}_{p} = | q_{p} | > 0$ dans le sens $↘$ des potentiels électriques, ceci étant conforme à ce qu'on attend :
Modèle:Allors du déplacement spontané du porteur de charge ${q^{'}}_{p} = | q_{p} | > 0$ son énergie potentielle électrique doit $↘$ ${$ comme l'énergie potentielle de pesanteur d'un objet ponctuel $↘$ spontanément quand il n'est soumis qu'à l'action du champ de pesanteur sans vitesse initiale $}$ et par suite son déplacement spontané doit se faire dans le sens des potentiels $↘$ ${$ comme le déplacement spontané d'un objet ponctuel soumis à la seule action du champ de pesanteur sans vitesse initiale se fait dans le sens du « potentiel de pesanteur $g z$ » $↘$ $($ l'appellation « potentiel de pesanteur » étant personnelle $)}$ et
Modèle:Allors du déplacement spontané du porteur de charge $q_{p} < 0$ son énergie potentielle électrique doit également $↘$ , ce qui correspond à un déplacement spontané dans le sens des potentiels $↗$ c.-à-d. effectivement en sens contraire du porteur de charge ${q^{'}}_{p} = | q_{p} | > 0$ .
↑ Retenir que le champ électrique est toujours dans le sens $↘$ du potentiel.
Modèle:AlSuite de la note « ³³ » $($ plus haut dans ce chapitre $)$ : le déplacement spontané du porteur de charge ${q^{'}}_{p} = | q_{p} | > 0$ devant se faire dans le sens des potentiels $↘$ , nous vérifions qu'il se fait effectivement dans le sens de $\vec{E} (M)$ et
Modèle:Al Modèle:Transparentcelui du porteur de charge $q_{p} < 0$ dans le sens des potentiels $↗$ , nous vérifions qu'il se fait effectivement dans le sens contraire de $\vec{E} (M)$ .
↑ C.-à-d. l'endroit où l'énergie potentielle est choisie nulle.
↑ On définira ultérieurement $($ autrement que par analogie $)$ le potentiel électrique à partir du champ électrique.
↑ Historiquement le qualificatif « continu » est synonyme de « permanent » ; cela n'ayant rien à voir avec la continuité en mathématique je conseille d'éviter ce qualificatif autant que possible.
↑ La borne notée « $-$ » étant celle au « plus bas potentiel ».
↑ Dans ce cas il ne s'agit pas de la borne au plus bas potentiel mais de la borne reliée à la masse du générateur servant de référence au potentiel $($ le plus souvent cette borne est reliée à la Terre par l'intermédiaire du fil de secteur $)$ .
↑ La borne notée « $+$ » étant celle au « plus haut potentiel ».
↑ Dans ce cas il ne s'agit pas de la borne au plus haut potentiel mais de la borne non reliée à la masse du générateur laquelle sert de référence au potentiel $($ si la masse du générateur est reliée à la Terre par l'intermédiaire du fil de secteur, la borne rouge est donc à un potentiel dont le signe dépend de la fonction espérée aux bornes du générateur $)$ .
↑ Toutefois on ne parle pas de « force électromotrice » car celle-ci a une autre signification $($ laquelle n'est absolument pas celle d'une force $)$ on dira « force due au champ électromoteur » s'exerçant sur le porteur de charge mobile.
↑ Ceci étant réalisé si le courant circulant dans le générateur est effectivement délivré par ce dernier.
↑ En effet il s'agit de la tension entre le conducteur intérieur $T$ du câble relié à la masse du générateur $($ laquelle est très souvent reliée à la Terre par l'intermédiaire du fil de secteur $)$ et le point $M$ du conducteur extérieur, les deux conducteurs étant séparés par un isolant.
↑ En effet le courant principal circule le long du conducteur extérieur de $S$ vers $R$ en fuyant partiellement à travers l'isolant vers le conducteur intérieur d'où l'intensité du courant dépendant de $M$ $($ le courant de fuite circulant à travers l'isolant est, quant à lui, transversal, et d'intensité très faible voire nulle si l'isolant était parfait $)$ .
↑ Plus précisément elle dépend de la « permittivité diélectrique relative » du diélectrique « $ε_{r} = \frac{ε}{ε_{0}} > 1$ » dans laquelle $ε$ est la permittivité diélectrique du milieu et $ε_{0}$ la permittivité diélectrique du vide ${$ la permittivité diélectrique relative du milieu caractérise l'effet d'« écran » de l'isolant $($ en effet deux charges ponctuelles interagissant entre elles selon une force inversement proportionnelle à $r^{2}$ et proportionnelle au produit des charges, la norme de la force est diminuée quand les charges ponctuelles sont séparées par l'isolant étudié, plus exactement divisée par $ε_{r}$ par rapport à celle qui existerait entre elles dans le vide $)}$ ;
Modèle:All'air a une permittivité diélectrique relative $≃ 1$ , mais certains milieux isolants peuvent avoir une permittivité diélectrique relative nettement plus élevée : exemple le verre $ε_{r} ≃ 7$ , les céramiques de $10$ à $3000$ $\dots$
↑ Pour observer une propagation, compte-tenu de la grande valeur de célérité maximale, il est nécessaire d'utiliser une longueur de câble coaxial suffisamment importante ; si on utilise un isolant de permittivité diélectrique relative égale à $7$ , la célérité chute d'un facteur $\sqrt{7}$ et elle devient approximativement égale à $110 000 k m \cdot s^{- 1}$ .
↑ Le plus souvent il s'agit d'une variation par rapport à l'absence de champ mais cela pourrait être aussi une variation par rapport à un champ permanent $($ même si cette dernière situation est très rare $)$ .
↑ La présence du champ électrique en un point $M$ se détecte en plaçant en $M$ une charge ponctuelle témoin $q$ et en cherchant l'éventuelle force électrique s'exerçant sur elle ; on en déduit $\vec{E} (M) = \frac{{\vec{F}}_{élec, q \leftarrow \vec{E}} (M)}{q}$ .
↑ La présence du champ magnétique en un point $M$ se détecte en plaçant en $M$ une charge ponctuelle témoin $q$ mobile de vecteur vitesse $\vec{V} (M)$ et en cherchant l'éventuelle force magnétique $($ de Lorentz $)$ ${\vec{F}}_{Lor, q \vec{V} \leftarrow \vec{B}} (M)$ s'exerçant sur elle ${$ voir le paragraphe « cas particuliers (de force de Lorentz exercée sur une charge ponctuelle mobile dans un champ électromagnétique donné) » du chap. $21$ de la leçon « Mécanique 1 (PCSI) » $}$ ; en faisant deux expériences avec des vitesses judicieusement choisies on pourra en déduire $\vec{B} (M)$ mais l'expression est nettement plus compliquée que celle permettant de déduire $\vec{E} (M)$ de la force électrique ${\vec{F}}_{élec, q \leftarrow \vec{E}} (M)$ ${$ voir le paragraphe « définition du vecteur champ magnétique par le vecteur force magnétique de Lorentz que subit une charge témoin mobile » du chap. $1$ de la leçon « Induction et forces de Laplace » $}$ .
Modèle:AlHendrik Antoon Lorentz (1853 - 1928) est un physicien néerlandais principalement connu pour ses travaux sur l'électromagnétisme, il a laissé son nom aux « transformations dites de Lorentz » $[$ en fait les équations définitives des transformations de Lorentz ont été formulées en $1905$ par Henri Poincaré après avoir été introduites sous forme tâtonnante par quelques physiciens dont Hendrik Lorentz dès $1892$ pour ce dernier $]$ , transformations utilisées dans la théorie de la relativité restreinte élaborée par Albert Einstein en $1905$ ; Hendrik Lorentz partagea, en $1902$ , le prix Nobel de physique avec Pieter Zeeman (1865 - 1943) physicien néerlandais pour leurs recherches sur l'influence du magnétisme sur les phénomènes radiatifs $[$ Pieter Zeeman ayant découvert l'effet qui porte son nom en $1886]$ .
Modèle:AlHenri Poincaré (1854 - 1912) mathématicien, physicien, philosophe et ingénieur français à qui on doit des résultats d'importance en calcul infinitésimal, des avancées sur le problème à trois corps qui font de lui un des fondateurs de l'étude qualitative des systèmes d'équations différentielles et de la théorie du chaos, une participation active à la théorie de la relativité restreinte ainsi qu'à la théorie des systèmes dynamiques $\dots$
Modèle:AlAlbert Einstein (1879 - 1955), physicien théoricien d'origine allemande, devenu apatride en $1896$ puis suisse en $1901$ ; on lui doit la théorie de la relativité restreinte publiée en $1905$ , la relativité générale en $1916$ ainsi que bien d'autres avancées dans le domaine de la mécanique quantique et la cosmologie ; il a reçu le prix Nobel de physique en $1921$ pour son explication de l'effet photoélectrique.
↑ $\vec{E} (M)$ est la composante électrique du champ et $\vec{B} (M)$ sa composante magnétique.
↑ Le champ électromagnétique étant, dans le vide, $⊥$ à la direction de propagation.
↑ C.-à-d. créée à une extrémité du milieu de propagation.
↑ Avec les unités « $f$ en $H z$ » et « $T$ en $s$ ».
↑ Une onde est définie comme un phénomène physique dans lequel une perturbation locale $($ c.-à-d. un signal $)$ se déplace dans l'espace sans qu'il y ait de déplacement de matière en moyenne ;
Modèle:Alpour une onde donnée il peut y avoir plusieurs signaux physiques transportés par l'onde, par exemple :
Modèle:Al $≻$ pour une onde acoustique dans un tuyau d'air, il y a deux signaux principaux transportés par l'onde, l'élongation d'une tranche d'air et la surpression qui lui est associée,
Modèle:Al $≻$ pour une onde électromagnétique, les signaux transportés sont le champ électrique ou magnétique ;
Modèle:Alpour qu'un signal physique soit transporté par l'onde, il doit être nul dans l'état de repos et apparaître avec la perturbation.
↑ Ce signal peut aussi être vectoriel par exemple s'il est transporté par une onde électromagnétique, il suffit alors de remplacer la grandeur scalaire $s$ par la grandeur vectorielle $\vec{A}$ où $\vec{A}$ représenterait le champ électrique ou le champ magnétique, mais ceci ne sera fait pratiquement que si le caractère vectoriel joue un rôle, sinon on conservera la notation $s$ .
↑ $ω$ est exprimée en $r a d \cdot s^{- 1}$ .
↑ Voir le paragraphe « deuxième développement en série de Fourier » du chap. $5$ de la leçon « Outils mathématiques pour la physique (PCSI) » ; on choisit le 2^ème développement ${$ voir les paragraphes « 2^ème développement en série de Fourier » et « « harmonique instantané complexe de rang n » du chap. $5$ de la leçon « Signaux physiques - bis (PCSI) » $}$ ;
Modèle:AlJean-Baptiste Joseph Fourier (1768 - 1830) mathématicien et physicien français connu pour ses travaux sur la décomposition de fonctions périodiques et leur application au problème de la propagation de la chaleur.
↑ ^58,0 ^58,1 ^58,2 ^58,3 ^58,4 et ^58,5 Encore appelé « carré ».
↑ ^59,00 ^59,01 ^59,02 ^59,03 ^59,04 ^59,05 ^59,06 ^59,07 ^59,08 et ^59,09 Un signal alterné $($ c.-à-d. périodique avec une alternance positive et une négative $)$ est dit « symétrique » si la durée de l'alternance positive est égale à celle de l'alternance négative.
↑ ^60,0 et ^60,1 Le signal étant tracé sur l'intervalle $] 0, T [$ est impair car sa valeur sur $] - \frac{T}{2}, 0 [$ est opposée à celle sur $] 0, \frac{T}{2} [$ ainsi que celle sur $] - T, - \frac{T}{2} [$ opposée à celle $] \frac{T}{2}, T [$ .
↑ ^61,0 et ^61,1 Erreur de référence : Balise <ref> incorrecte : aucun texte n’a été fourni pour les références nommées spectre d'amplitudes
↑ L'amplitude de la réponse du filtre au signal d'entrée s'obtient en multipliant l'amplitude du signal d'entrée par le « gain du filtre pour la fréquence considérée » et
Modèle:Alla phase à l'origine de la réponse du filtre au signal d'entrée s'obtient en ajoutant à la phase à l'origine du signal d'entrée le déphasage du filtre pour la fréquence considérée, déphasage que l'on appelle « phase du filtre pour la fréquence considérée » ;
Modèle:Alpour les notions de gain $($ et de phase $)$ de filtre ${$ dispositif électronique caractérisé par une fonction de transfert $}$ , voir le paragraphe « définition d'une fonction de transfert harmonique d'un Q.L.P. fermé sur une charge et alimenté en entrée par une source fonctionnant en r.s.f. » du chap. $6$ de la leçon « Signaux physiques - bis (PCSI) ».
↑ Ceci constituant le théorème de superposition applicable à tout phénomène linéaire reliant causes à effets : « si à chaque cause ${cause}_{k}$ prise isolément on observe un effet ${effet}_{k}$ par un phénomène linéaire », « l'action de l'ensemble des causes prises simultanément $\sum_{k} {cause}_{k}$ aura pour effet, par le phénomène linéaire précédent, l'ensemble des effets $\sum_{k} {effet}_{k}$ ».
↑ Erreur de référence : Balise <ref> incorrecte : aucun texte n’a été fourni pour les références nommées Fourier
↑ L'addition manuelle serait très laborieuse $($ sauf dans le cas peu fréquent où il n'y aurait que deux ou trois harmoniques $)$ et de toute façon prendrait énormément de temps d'où la nécessité de la réaliser grâce à un logiciel.
↑ ^66,0 et ^66,1 Si on est plus exigeant.
↑ Peu d'harmoniques sont nécessaires car la forme du signal triangulaire est très proche de celle d'un signal sinusoïdal ; cela se justifie aussi par le fait que l'amplitude des harmoniques d'un signal triangulaire varie très rapidement en $\frac{1}{n^{2}}$ .
↑ Un nombre important d'harmoniques est nécessaire car la forme du signal créneau est assez éloignée de celle d'un signal sinusoïdal ; cela se justifie aussi par le fait que l'amplitude des harmoniques d'un signal créneau varie assez lentement en $\frac{1}{n}$ .
↑ ^69,0 et ^69,1 Basse Fréquence.
↑ ^70,0 et ^70,1 Haute Fréquence.
↑ Intervalle séparant deux sons dont la fréquence fondamentale du plus aigu est le double de celle du plus grave.
↑ ^72,0 et ^72,1 Ultraviolet.
↑ Au-dessous de $9 1 0^{3} H z$ ce sont encore des ondes radio mais elles ne sont pas réglementées.
↑ Grandes Ondes.
↑ Modulation d'Amplitude.
↑ Modulation de Fréquence.
↑ Global Positioning System.
↑ Wireless Fidelity.
↑ ^79,0 et ^79,1 Préfixes multiplicateurs : $P$ ou « Peta » $= 1 0^{15}$ et $E$ ou « Exa » $= 1 0^{18}$ $($ il y a encore $T$ ou « Téra » $= 1 0^{12}$ , $G$ ou « Giga » $= 1 0^{9}$ $\dots)$
↑ On réserve usuellement le nom de « rayons gamma » $($ noté $γ)$ aux rayonnements issus de l'annihilation d'une paire électron-positron, dans les autres cas on parle plutôt de « rayonnements gamma » $($ noté $γ)$ .

Modèle:Bas de page

[fluide-1] 1,0 et ^1,1 c.-à-d. liquide ou gazeux.

[2] Et aussi les liquides très visqueux.

[3] $\vec{n}$ est un vecteur unitaire $⊥$ à $S$ , dirigé vers l'intérieur de l'objet.

[4] $\vec{τ}$ est un vecteur unitaire tangentiel à $S$ , choisi dans le plan contenant $\vec{F}$ et $\vec{n}$ .

[5] La pression atmosphérique dans les conditions usuelles d'altitude et de température étant au voisinage de $1 0^{5} P a$ , on utilise une unité dérivée « le bar » dont la conversion est $1 b a r = 1 0^{5} P a$ .

[liquide_normal-6] 6,0 ^6,1 ^6,2 et ^6,3 Dans cette catégorie on exclut les liquides très visqueux pour lesquels on observe aussi un signal transversal.

[liquide_très_visqueux-7] 7,0 et ^7,1 La très grande viscosité dans un liquide fait que ce dernier a un comportement plus proche de celui d'un solide que de celui d'un liquide « normal » $($ revoir la note « ⁷ » plus haut dans ce chapitre justifiant le qualificatif « normal » $)$ .

[8] De même homogénéité qu'une surpression, s'exprimant en $P a$ et le plus souvent en un multiple le $M P a = 1 0^{6} P a = 10 b a r$ .

[9] Dans une même surface transversale $𝒮$ , si la surface transversale de droite $𝒮_{d}$ est décalée vers le haut par rapport à la surface $𝒮$ considérée, $𝒮_{d}$ exerce une force vers le haut sur $𝒮$ de composante $F_{⊥}$ et si la surface transversale de gauche $𝒮_{g}$ est décalée vers le bas par rapport à la surface $𝒮$ considérée, $𝒮_{g}$ exerce une force vers le bas sur $𝒮$ de composante $- F_{⊥}$ .

[10] Un gaz a une masse volumique plus faible qu'un liquide dans les mêmes conditions de température et de pression, approximativement d'un facteur $1000$ .

[11] La densité et l'élasticité ont des effets contraires sur la célérité, l'augmentation de la densité a pour effet de diminuer la célérité de propagation alors que la diminution de l'élasticité pour effet d'augmenter cette célérité, les liquides étant plus denses mais moins élastiques que les gaz, on remarque donc que l'effet de l'élasticité est prépondérant.

[12] La grandeur électrique peut être une tension ou une intensité de courant ; sa variation peut être constatée par rapport à son absence $($ de tension ou d'intensité $)$ ou par rapport à une tension ou intensité permanente, cette dernière constituant la valeur dite de « repos » ou de « polarisation ».

[13] Les éléments chargés fixes comme il peut en exister dans les milieux non fluides $($ c.-à-d. solides $)$ ne jouant aucun rôle dans la conduction.

[14] La densité volumique particulaire a pour ordre de grandeur $N_{V, m} ≃ 1 0^{28} m^{- 3}$ , calcul exposé ci-après dans le cas du cuivre.

[15] La densité volumique particulaire dépend de la concentration de la solution mais usuellement elle ne dépasse pas $N_{V, m} ≃ 1 0^{25} m^{- 3}$ , calcul exposé dans le cas d'une solution décimolaire de chlorure de sodium et dans le cas de l'eau pure $($ très mauvais conducteur $)$ .

[16] Un semi-conducteur intrinsèque est un semi-conducteur pur $($ par exemple du silicium $S i)$ , il est isolant à basse température $($ un isolant ayant une densité volumique particulaire $≲ 1 0^{7} m^{- 3})$ et mauvais conducteur à température ordinaire $($ seuls quelques électrons de valence ont suffisamment d'énergie pour devenir des électrons de conduction, ils laissent alors derrière eux un site de valence vide et un électron de valence des atomes voisins peut venir l'occuper laissant à son tour derrière lui son site initial de valence vide $)$ ;
Modèle:Alpour simplifier l'étude $($ pour qu'il n'y ait pas deux types de porteurs de charge négative mobiles « les électrons de conduction » et « les électrons de valence sautant d'un site occupé à un site vide » $)$ les électroniciens considèrent qu'aucun électron de valence ne peut migrer, les sites de valence restant tous occupés $($ pour les sites réellement vides, conséquence d'un électron de valence devenu électron de conduction, l'électron de conduction restant mobile ils ajoutent fictivement un électron de valence sans possibilité de migrer et ils y superposent une particule fictive mobile de charge positive qu'ils appellent « trou » $)$ du point de vue électrique ils ajoutent donc fictivement une charge nulle $($ avec la propriété suivante : la superposition d'un « trou » et d'un « électron de valence » est équivalente à un site vide $)$ ;
Modèle:Alils remplacent alors la migration d'un électron de valence d'un site occupé $(1)$ à un site vide $(2)$ par la migration d'un trou du site $(2)$ au site $(1)$ , le départ du trou du site $(2)$ découvrant l'électron de valence et le rendant réel alors que l'arrivée du trou sur le site $(1)$ couvrant l'électron de valence et rendant ce dernier fictif, la superposition étant équivalente à un site vide ;
Modèle:Alil y a donc deux types de porteurs de charge mobiles : les « électrons de conduction » et les « trous » en quantités égales.
Modèle:AlLa densité volumique particulaire à température ordinaire est nettement plus faible que dans un métal $N_{V, m} ≃ 1 0^{16} m^{- 3}$ et elle est quasi-nulle à basse température.

[17] Un semi-conducteur extrinsèque dopé $N$ est un semi-conducteur $($ par exemple $S i)$ dans lequel on a ajouté des impuretés pentavalentes $($ par exemple d'arsenic $A s)$ ${$ on rappelle la définition de la valence d'un élément : nombre d'électrons de valence qui peuvent être cédés ou captés pour que la couche de valence devienne vide ou complètement remplie $}$ l'électron supplémentaire par rapport au semi-conducteur tétravalent pouvant relativement aisément se déplacer, il constitue le porteur de charge mobile, la densité volumique particulaire ayant pour ordre de grandeur $N_{V, m} ≃ 1 0^{22} m^{- 3}$ ${$ on peut ainsi négliger la semi-conduction intrinsèque $}$ .

[18] Un semi-conducteur extrinsèque dopé $P$ est un semi-conducteur $($ par exemple $S i)$ dans lequel on a ajouté des impuretés trivalentes $($ par exemple de gallium $G a)$ , le site de l'électron « manquant » par rapport au semi-conducteur tétravalent est remplacé par la présence simultanée d'un électron de valence fictif et d'un trou fictif, et comme dans un semi-conducteur intrinsèque les électrons de valence ajoutés restent fixes et les trous peuvent se déplacer pour « recouvrir » d'autres électrons de valence, les trous constituant donc les porteurs de charge mobiles, la densité volumique particulaire ayant le même ordre de grandeur que dans les semi-conducteurs dopés $N$ , $N_{V, m} ≃$ $1 0^{22} m^{- 3}$ ${$ on peut ainsi négliger la semi-conduction intrinsèque $}$ .

[19] La masse volumique de l'eau vaut $μ_{eau} = 1000 k g \cdot m^{- 3}$ .

[Avogadro-20] Lorenzo Romano Amedeo Carlo Avogadro (1776 - 1856) est un physicien et chimiste du Piémont $($ région actuelle de l'Italie $)$ à qui on doit essentiellement la loi d'Avogadro Ampère qu'il énonça en $1811$ et proposée indépendamment par Ampère en $1814$ , celle-ci spécifiant que « des volumes égaux de gaz parfaits différents, aux mêmes conditions de température et de pression, contiennent le même nombre de molécules ».
Modèle:AlAndré-Marie Ampère (1775 - 1836), mathématicien, physicien, chimiste et philosophe français, peut être considéré comme l'un des premiers artisans de la mathématisation de la physique, il a édifié les fondements théoriques de l'électromagnétisme et a découvert les bases de l'électronique de la matière.

[21] En physique l'unité de volume du S.I. $($ Système international $)$ est le $m^{3}$ et non le $L$ .

[22] L'ion oxonium est encore appelé ion hydronium.

[23] Il s'agit en fait de la même grandeur mais la première est utilisée en chimie et la seconde en physique $($ pour souligner la différence d'utilisation nous adoptons des noms différents ainsi que des notations différentes $)$ ; de plus les unités employées ne sont pas les mêmes ${$ on rappelle que l'unité de volume dans le S.I. $($ Système international $)$ est le $m^{3}$ et non le $L}$ .

[24] Ce sens est qualifié de « conventionnel » car, dans la plupart des matériaux conduisant plus ou moins l'électricité, il y a deux types de porteurs de charge mobiles circulant en sens inverse $($ quand un mouvement d'ensemble est imposé $)$ , il y avait donc deux choix possibles ; c'est en $1820$ que le français Ampère définit la grandeur « courant » matérialisée par la circulation des deux types de porteurs de charge mobiles en définissant, par convention, le sens du courant comme le sens de circulation de l'un des types de porteurs de charge mobiles, les porteurs de charge mobiles de signe opposé correspondant au sens contraire du courant $\dots$ mais le choix aurait pu être l'inverse, il s'agit donc d'un choix historique ;
Modèle:AlAndré-Marie Ampère (1775 - 1836), mathématicien, physicien, chimiste et philosophe français, peut être considéré comme l'un des 1^ers artisans de la mathématisation de la physique, il a édifié les fondements théoriques de l'électromagnétisme et a découvert les bases de l'électronique de la matière.

[25] Pour qu'il y ait déplacement d'ensemble de porteurs de charge mobiles il faut que le conducteur soit branché dans un circuit dans lequel il y a au moins un générateur qui lui impose une tension entre ses bornes $($ cette notion de tension est vue ultérieurement dans les paragraphes « nécessité d'imposer une tension aux bornes d'un récepteur pour qu'il soit traversé par un courant » et « tension aux bornes d'un générateur et sens du courant dans ce dernier » plus loin dans ce chapitre $)$ .

[26] $d t$ est appelée « durée élémentaire » et correspond à l'élément différentiel de temps, voir le paragraphe « élément différentiel d'une variable » du chap. $4$ de la leçon « Outils mathématiques pour la physique (PCSI) ».

[27] $d q$ correspond à l'élément différentiel de charge, voir le paragraphe « élément différentiel d'une variable » du chap. $4$ de la leçon « Outils mathématiques pour la physique (PCSI) » ;
Modèle:Alen fait à l'échelle microscopique, la charge n'est pas une grandeur continue mais quantifiée, elle est toujours un multiple de la charge élémentaire $e ≃ 1, 6 1 0^{- 19} C$ , mais à l'échelle macroscopique ${$ ou mésoscopique $($ un échantillon est d'échelle mésoscopique s'il est de dimensions infiniment petites à l'échelle macroscopique mais infiniment grandes à l'échelle Modèle:Nobr toute charge comprenant un grande nombre de charges élémentaires $\Rightarrow$ chaque charge élémentaire peut être considérée comme quasi-nulle ce qui revient à envisager le caractère continu de la charge.

[28] Les énergies potentielles seront notées $U$ sauf quand il y a risque de confusion, ce qui est le cas en électricité, $U$ étant réservée à la tension.

[choix_de_qp_positive-29] 29,0 et ^29,1 On se limite au choix de $q_{p} > 0$ car on souhaite d'induire une formule pour l'énergie potentielle électrique de la charge $q_{p}$ dans le champ électrique $\vec{E}$ par analogie avec celle d'un objet ponctuel de masse $m$ $($ nécessairement $> 0)$ dans le champ de pesanteur $\vec{g}$ .

[30] Avec cette formule, l'énergie potentielle étant choisie nulle au niveau du sol, on dit que sa référence est le sol.

[potentiel_de_pesanteur-31] 31,0 ^31,1 et ^31,2 Mais cette notion de « potentiel de pesanteur au point $M$ » n'est quasiment jamais introduite $($ de plus il s'agit d'une appellation personnelle $)$ .

[32] En un point $M$ de potentiel $V (M)$ , un porteur de charge $q_{p} < 0$ ayant une énergie potentielle électrique opposée à celle d'un porteur de charge ${q^{'}}_{p} = | q_{p} | > 0$ , la décroissance de l'énergie potentielle électrique du porteur de charge $q_{p} < 0$ se fait dans le sens $↗$ des potentiels électriques alors que celle de l'énergie potentielle électrique du porteur de charge ${q^{'}}_{p} = | q_{p} | > 0$ dans le sens $↘$ des potentiels électriques, ceci étant conforme à ce qu'on attend :
Modèle:Allors du déplacement spontané du porteur de charge ${q^{'}}_{p} = | q_{p} | > 0$ son énergie potentielle électrique doit $↘$ ${$ comme l'énergie potentielle de pesanteur d'un objet ponctuel $↘$ spontanément quand il n'est soumis qu'à l'action du champ de pesanteur sans vitesse initiale $}$ et par suite son déplacement spontané doit se faire dans le sens des potentiels $↘$ ${$ comme le déplacement spontané d'un objet ponctuel soumis à la seule action du champ de pesanteur sans vitesse initiale se fait dans le sens du « potentiel de pesanteur $g z$ » $↘$ $($ l'appellation « potentiel de pesanteur » étant personnelle $)}$ et
Modèle:Allors du déplacement spontané du porteur de charge $q_{p} < 0$ son énergie potentielle électrique doit également $↘$ , ce qui correspond à un déplacement spontané dans le sens des potentiels $↗$ c.-à-d. effectivement en sens contraire du porteur de charge ${q^{'}}_{p} = | q_{p} | > 0$ .

[33] Retenir que le champ électrique est toujours dans le sens $↘$ du potentiel.
Modèle:AlSuite de la note « ³³ » $($ plus haut dans ce chapitre $)$ : le déplacement spontané du porteur de charge ${q^{'}}_{p} = | q_{p} | > 0$ devant se faire dans le sens des potentiels $↘$ , nous vérifions qu'il se fait effectivement dans le sens de $\vec{E} (M)$ et
Modèle:Al Modèle:Transparentcelui du porteur de charge $q_{p} < 0$ dans le sens des potentiels $↗$ , nous vérifions qu'il se fait effectivement dans le sens contraire de $\vec{E} (M)$ .

[référence_d'une_énergie_potentielle-34] C.-à-d. l'endroit où l'énergie potentielle est choisie nulle.

[35] On définira ultérieurement $($ autrement que par analogie $)$ le potentiel électrique à partir du champ électrique.

[36] Historiquement le qualificatif « continu » est synonyme de « permanent » ; cela n'ayant rien à voir avec la continuité en mathématique je conseille d'éviter ce qualificatif autant que possible.

[37] La borne notée « $-$ » étant celle au « plus bas potentiel ».

[38] Dans ce cas il ne s'agit pas de la borne au plus bas potentiel mais de la borne reliée à la masse du générateur servant de référence au potentiel $($ le plus souvent cette borne est reliée à la Terre par l'intermédiaire du fil de secteur $)$ .

[39] La borne notée « $+$ » étant celle au « plus haut potentiel ».

[40] Dans ce cas il ne s'agit pas de la borne au plus haut potentiel mais de la borne non reliée à la masse du générateur laquelle sert de référence au potentiel $($ si la masse du générateur est reliée à la Terre par l'intermédiaire du fil de secteur, la borne rouge est donc à un potentiel dont le signe dépend de la fonction espérée aux bornes du générateur $)$ .

[41] Toutefois on ne parle pas de « force électromotrice » car celle-ci a une autre signification $($ laquelle n'est absolument pas celle d'une force $)$ on dira « force due au champ électromoteur » s'exerçant sur le porteur de charge mobile.

[42] Ceci étant réalisé si le courant circulant dans le générateur est effectivement délivré par ce dernier.

[43] En effet il s'agit de la tension entre le conducteur intérieur $T$ du câble relié à la masse du générateur $($ laquelle est très souvent reliée à la Terre par l'intermédiaire du fil de secteur $)$ et le point $M$ du conducteur extérieur, les deux conducteurs étant séparés par un isolant.

[44] En effet le courant principal circule le long du conducteur extérieur de $S$ vers $R$ en fuyant partiellement à travers l'isolant vers le conducteur intérieur d'où l'intensité du courant dépendant de $M$ $($ le courant de fuite circulant à travers l'isolant est, quant à lui, transversal, et d'intensité très faible voire nulle si l'isolant était parfait $)$ .

[45] Plus précisément elle dépend de la « permittivité diélectrique relative » du diélectrique « $ε_{r} = \frac{ε}{ε_{0}} > 1$ » dans laquelle $ε$ est la permittivité diélectrique du milieu et $ε_{0}$ la permittivité diélectrique du vide ${$ la permittivité diélectrique relative du milieu caractérise l'effet d'« écran » de l'isolant $($ en effet deux charges ponctuelles interagissant entre elles selon une force inversement proportionnelle à $r^{2}$ et proportionnelle au produit des charges, la norme de la force est diminuée quand les charges ponctuelles sont séparées par l'isolant étudié, plus exactement divisée par $ε_{r}$ par rapport à celle qui existerait entre elles dans le vide $)}$ ;
Modèle:All'air a une permittivité diélectrique relative $≃ 1$ , mais certains milieux isolants peuvent avoir une permittivité diélectrique relative nettement plus élevée : exemple le verre $ε_{r} ≃ 7$ , les céramiques de $10$ à $3000$ $\dots$

[46] Pour observer une propagation, compte-tenu de la grande valeur de célérité maximale, il est nécessaire d'utiliser une longueur de câble coaxial suffisamment importante ; si on utilise un isolant de permittivité diélectrique relative égale à $7$ , la célérité chute d'un facteur $\sqrt{7}$ et elle devient approximativement égale à $110 000 k m \cdot s^{- 1}$ .

[47] Le plus souvent il s'agit d'une variation par rapport à l'absence de champ mais cela pourrait être aussi une variation par rapport à un champ permanent $($ même si cette dernière situation est très rare $)$ .

[48] La présence du champ électrique en un point $M$ se détecte en plaçant en $M$ une charge ponctuelle témoin $q$ et en cherchant l'éventuelle force électrique s'exerçant sur elle ; on en déduit $\vec{E} (M) = \frac{{\vec{F}}_{élec, q \leftarrow \vec{E}} (M)}{q}$ .

[49] La présence du champ magnétique en un point $M$ se détecte en plaçant en $M$ une charge ponctuelle témoin $q$ mobile de vecteur vitesse $\vec{V} (M)$ et en cherchant l'éventuelle force magnétique $($ de Lorentz $)$ ${\vec{F}}_{Lor, q \vec{V} \leftarrow \vec{B}} (M)$ s'exerçant sur elle ${$ voir le paragraphe « cas particuliers (de force de Lorentz exercée sur une charge ponctuelle mobile dans un champ électromagnétique donné) » du chap. $21$ de la leçon « Mécanique 1 (PCSI) » $}$ ; en faisant deux expériences avec des vitesses judicieusement choisies on pourra en déduire $\vec{B} (M)$ mais l'expression est nettement plus compliquée que celle permettant de déduire $\vec{E} (M)$ de la force électrique ${\vec{F}}_{élec, q \leftarrow \vec{E}} (M)$ ${$ voir le paragraphe « définition du vecteur champ magnétique par le vecteur force magnétique de Lorentz que subit une charge témoin mobile » du chap. $1$ de la leçon « Induction et forces de Laplace » $}$ .
Modèle:AlHendrik Antoon Lorentz (1853 - 1928) est un physicien néerlandais principalement connu pour ses travaux sur l'électromagnétisme, il a laissé son nom aux « transformations dites de Lorentz » $[$ en fait les équations définitives des transformations de Lorentz ont été formulées en $1905$ par Henri Poincaré après avoir été introduites sous forme tâtonnante par quelques physiciens dont Hendrik Lorentz dès $1892$ pour ce dernier $]$ , transformations utilisées dans la théorie de la relativité restreinte élaborée par Albert Einstein en $1905$ ; Hendrik Lorentz partagea, en $1902$ , le prix Nobel de physique avec Pieter Zeeman (1865 - 1943) physicien néerlandais pour leurs recherches sur l'influence du magnétisme sur les phénomènes radiatifs $[$ Pieter Zeeman ayant découvert l'effet qui porte son nom en $1886]$ .
Modèle:AlHenri Poincaré (1854 - 1912) mathématicien, physicien, philosophe et ingénieur français à qui on doit des résultats d'importance en calcul infinitésimal, des avancées sur le problème à trois corps qui font de lui un des fondateurs de l'étude qualitative des systèmes d'équations différentielles et de la théorie du chaos, une participation active à la théorie de la relativité restreinte ainsi qu'à la théorie des systèmes dynamiques $\dots$
Modèle:AlAlbert Einstein (1879 - 1955), physicien théoricien d'origine allemande, devenu apatride en $1896$ puis suisse en $1901$ ; on lui doit la théorie de la relativité restreinte publiée en $1905$ , la relativité générale en $1916$ ainsi que bien d'autres avancées dans le domaine de la mécanique quantique et la cosmologie ; il a reçu le prix Nobel de physique en $1921$ pour son explication de l'effet photoélectrique.

[50] $\vec{E} (M)$ est la composante électrique du champ et $\vec{B} (M)$ sa composante magnétique.

[51] Le champ électromagnétique étant, dans le vide, $⊥$ à la direction de propagation.

[52] C.-à-d. créée à une extrémité du milieu de propagation.

[53] Avec les unités « $f$ en $H z$ » et « $T$ en $s$ ».

[54] Une onde est définie comme un phénomène physique dans lequel une perturbation locale $($ c.-à-d. un signal $)$ se déplace dans l'espace sans qu'il y ait de déplacement de matière en moyenne ;
Modèle:Alpour une onde donnée il peut y avoir plusieurs signaux physiques transportés par l'onde, par exemple :
Modèle:Al $≻$ pour une onde acoustique dans un tuyau d'air, il y a deux signaux principaux transportés par l'onde, l'élongation d'une tranche d'air et la surpression qui lui est associée,
Modèle:Al $≻$ pour une onde électromagnétique, les signaux transportés sont le champ électrique ou magnétique ;
Modèle:Alpour qu'un signal physique soit transporté par l'onde, il doit être nul dans l'état de repos et apparaître avec la perturbation.

[55] Ce signal peut aussi être vectoriel par exemple s'il est transporté par une onde électromagnétique, il suffit alors de remplacer la grandeur scalaire $s$ par la grandeur vectorielle $\vec{A}$ où $\vec{A}$ représenterait le champ électrique ou le champ magnétique, mais ceci ne sera fait pratiquement que si le caractère vectoriel joue un rôle, sinon on conservera la notation $s$ .

[56] $ω$ est exprimée en $r a d \cdot s^{- 1}$ .

[57] Voir le paragraphe « deuxième développement en série de Fourier » du chap. $5$ de la leçon « Outils mathématiques pour la physique (PCSI) » ; on choisit le 2^ème développement ${$ voir les paragraphes « 2^ème développement en série de Fourier » et « « harmonique instantané complexe de rang n » du chap. $5$ de la leçon « Signaux physiques - bis (PCSI) » $}$ ;
Modèle:AlJean-Baptiste Joseph Fourier (1768 - 1830) mathématicien et physicien français connu pour ses travaux sur la décomposition de fonctions périodiques et leur application au problème de la propagation de la chaleur.

[carré-58] 58,0 ^58,1 ^58,2 ^58,3 ^58,4 et ^58,5 Encore appelé « carré ».

[signal_symétrique-59] 59,00 ^59,01 ^59,02 ^59,03 ^59,04 ^59,05 ^59,06 ^59,07 ^59,08 et ^59,09 Un signal alterné $($ c.-à-d. périodique avec une alternance positive et une négative $)$ est dit « symétrique » si la durée de l'alternance positive est égale à celle de l'alternance négative.

[signal_impair-60] 60,0 et ^60,1 Le signal étant tracé sur l'intervalle $] 0, T [$ est impair car sa valeur sur $] - \frac{T}{2}, 0 [$ est opposée à celle sur $] 0, \frac{T}{2} [$ ainsi que celle sur $] - T, - \frac{T}{2} [$ opposée à celle $] \frac{T}{2}, T [$ .

[spectre_d'amplitudes-61] 61,0 et ^61,1 Erreur de référence : Balise <ref> incorrecte : aucun texte n’a été fourni pour les références nommées spectre d'amplitudes

[62] L'amplitude de la réponse du filtre au signal d'entrée s'obtient en multipliant l'amplitude du signal d'entrée par le « gain du filtre pour la fréquence considérée » et
Modèle:Alla phase à l'origine de la réponse du filtre au signal d'entrée s'obtient en ajoutant à la phase à l'origine du signal d'entrée le déphasage du filtre pour la fréquence considérée, déphasage que l'on appelle « phase du filtre pour la fréquence considérée » ;
Modèle:Alpour les notions de gain $($ et de phase $)$ de filtre ${$ dispositif électronique caractérisé par une fonction de transfert $}$ , voir le paragraphe « définition d'une fonction de transfert harmonique d'un Q.L.P. fermé sur une charge et alimenté en entrée par une source fonctionnant en r.s.f. » du chap. $6$ de la leçon « Signaux physiques - bis (PCSI) ».

[63] Ceci constituant le théorème de superposition applicable à tout phénomène linéaire reliant causes à effets : « si à chaque cause ${cause}_{k}$ prise isolément on observe un effet ${effet}_{k}$ par un phénomène linéaire », « l'action de l'ensemble des causes prises simultanément $\sum_{k} {cause}_{k}$ aura pour effet, par le phénomène linéaire précédent, l'ensemble des effets $\sum_{k} {effet}_{k}$ ».

[Fourier-64] Erreur de référence : Balise <ref> incorrecte : aucun texte n’a été fourni pour les références nommées Fourier

[65] L'addition manuelle serait très laborieuse $($ sauf dans le cas peu fréquent où il n'y aurait que deux ou trois harmoniques $)$ et de toute façon prendrait énormément de temps d'où la nécessité de la réaliser grâce à un logiciel.

[Exigence-66] 66,0 et ^66,1 Si on est plus exigeant.

[67] Peu d'harmoniques sont nécessaires car la forme du signal triangulaire est très proche de celle d'un signal sinusoïdal ; cela se justifie aussi par le fait que l'amplitude des harmoniques d'un signal triangulaire varie très rapidement en $\frac{1}{n^{2}}$ .

[68] Un nombre important d'harmoniques est nécessaire car la forme du signal créneau est assez éloignée de celle d'un signal sinusoïdal ; cela se justifie aussi par le fait que l'amplitude des harmoniques d'un signal créneau varie assez lentement en $\frac{1}{n}$ .

[B.F.-69] 69,0 et ^69,1 Basse Fréquence.

[H.F.-70] 70,0 et ^70,1 Haute Fréquence.

[71] Intervalle séparant deux sons dont la fréquence fondamentale du plus aigu est le double de celle du plus grave.

[UV-72] 72,0 et ^72,1 Ultraviolet.

[73] Au-dessous de $9 1 0^{3} H z$ ce sont encore des ondes radio mais elles ne sont pas réglementées.

[G.O.-74] Grandes Ondes.

[AM-75] Modulation d'Amplitude.

[FM-76] Modulation de Fréquence.

[G.P.S.-77] Global Positioning System.

[Wi-Fi-78] Wireless Fidelity.

[Préfixes_multiplicateurs-79] 79,0 et ^79,1 Préfixes multiplicateurs : $P$ ou « Peta » $= 1 0^{15}$ et $E$ ou « Exa » $= 1 0^{18}$ $($ il y a encore $T$ ou « Téra » $= 1 0^{12}$ , $G$ ou « Giga » $= 1 0^{9}$ $\dots)$

[80] On réserve usuellement le nom de « rayons gamma » $($ noté $γ)$ aux rayonnements issus de l'annihilation d'une paire électron-positron, dans les autres cas on parle plutôt de « rayonnements gamma » $($ noté $γ)$ .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[79]

[80]

Signaux physiques (PCSI)/Propagation d'un signal : Exemples de signaux, spectre

Signal mécanique transversal ou longitudinal, célérité de propagation

Grandeurs vibrantes en acoustique, célérité de la propagation

Notion de pression en mécanique

Les deux principales grandeurs vibrantes en acoustique

Célérité de propagation d'un signal acoustique

Grandeurs vibrantes en électricité, célérité de la propagation

Notion d'intensité de courant et de tension

Notion de conducteur, isolant, semi-conducteur

Évaluation de la densité volumique particulaire des porteurs de charge mobiles dans quelques conducteurs typiques

Modélisation filiforme d'un conducteur, sens conventionnel du courant

Définition de l'intensité algébrique du courant

Nécessité d'imposer une tension aux bornes d'un récepteur pour qu'il soit traversé par un courant

Tension aux bornes d'un générateur et sens du courant dans ce dernier

Les deux principales grandeurs vibrantes en électricité

Célérité de propagation d'un signal électrique

Grandeurs vibrantes en électromagnétisme, célérité de la propagation

Notion de champ électromagnétique

Milieu de propagation et grandeur vibrante

Célérité de propagation d'un signal électromagnétique

Limitation de l'étude aux grandeurs vibrantes périodiques

Exemple de signal périodique sinusoïdal

Analyse spectrale d'un signal périodique

Exemple d'un signal créneau symétrique

Exemple d'un signal triangulaire symétrique

Notion de filtrage linéaire et réponse fréquentielle du filtre à un signal périodique

Notion de filtre linéaire

Réponse fréquentielle du filtre (linéaire) à un signal d'entrée périodique

Synthèse spectrale (de Fourier) permettant de trouver le signal périodique à partir de sa représentation fréquentielle

Filtre passe-bas idéal

Nombre minimal de premiers harmoniques nécessaire pour reconstruire un signal triangulaire symétrique

Nombre minimal de premiers harmoniques nécessaire pour reconstruire un signal créneau symétrique

Ordre de grandeur des fréquences dans les domaines acoustique et électromagnétique

Domaine acoustique

Domaine électromagnétique

Ondes lumineuses

Ondes hertziennes (ou radioélectriques)

Rayons X

Rayonnements gamma

Notes et références

Menu de navigation

Rechercher