Signaux physiques (PCSI)/Introduction au monde quantique : oscillateur harmonique
En compléments : opérateurs linéaires « énergie potentielle », « énergie cinétique non relativiste » et « hamiltonien », équation de Schrödinger (applicable en mécanique quantique non relativiste)
Opérateur linéaire « énergie potentielle » d'une particule quantique
Modèle:AlÀ la grandeur « énergie potentielle » de la particule « quantique », on associe l'opérateur linéaire « énergie potentielle » «»,
Modèle:All'action de cet opérateur linéaire
sur la fonction d'onde
qui modélise l'état de la particule « quantique »
Modèle:AlModèle:Transparentdonnant la valeur
à l'énergie potentielle de la particule dont l'état est décrit par la fonction d'onde
[1],
Opérateur linéaire « énergie cinétique non relativiste » d'une particule quantique massique
Modèle:AlÀ la grandeur « énergie cinétique non relativiste » de la particule « quantique » massique où est la masse de la particule et
Modèle:AlModèle:Transparent sa quantité de mouvement non relativiste[2], on associe
Modèle:AlModèle:Transparentl'opérateur linéaire « énergie cinétique non relativiste » défini selon «»[3] soit ou «»[4],
Modèle:All'action de cet opérateur linéaire
sur la fonction d'onde décrivant un état de la particule « quantique » non relativiste[5] pour lequel l'énergie cinétique est fixée
Modèle:AlModèle:Transparentdonnant toutes les valeurs possibles d'énergie cinétique non relativiste de la particule dont l'état est décrit par la fonction d'onde particulière
[6], soit
Opérateur linéaire « hamiltonien » d'une particule quantique massique non relativiste
Introduction : notion d'« hamiltonien » en mécanique analytique
Modèle:AlLa notion d'« hamiltonien » d'une particule classique a été introduite par William Rowan Hamilton[7] en lors de la création de la mécanique hamiltonienne, qui est une reformulation de la mécanique lagrangienne créée par Joseph-Louis Lagrange[8] à partir de , elle-même une reformulation de la mécanique newtonienne
Mécanique lagrangienne
Modèle:AlDans le cadre de la mécanique classique, le lagrangien d'une particule squelette de la mécanique lagrangienne est une fonction de sa position , de et du temps , toutes variables supposées indépendantes[9], défini par «»[10] ;
Modèle:Alà partir du lagrangien de la particule, on obtient les équations du mouvement de cette dernière en écrivant que l'« action » sur définie par «»[11]
Modèle:AlModèle:Transparentest stationnaire sur la trajectoire[12], plus exactement
Modèle:AlModèle:Transparenton obtient d'abord les équations d'Euler-Lagrange[13]Modèle:,[8] «» voir l'établissement dans l'encart ci-dessous,
Modèle:Encart
Modèle:AlModèle:Transparentpuis on déduit les équations du mouvement en explicitant les équations d'Euler-Lagrange[13]Modèle:,[8] «» dans lesquelles Modèle:Nobr » ainsi que «» d'où «» soit
Modèle:AlModèle:Transparentfinalement l'équation vectorielle du mouvement de la particule «»[14] dans laquelle est le vecteur accélération de la particule ou, en utilisant le lien entre la force appliquée à la particule et l'énergie potentielle dont elle dérive «»[15],
Modèle:AlModèle:Transparentl'équation différentielle du 2ème ordre régissant le mouvement de la particule «».
Mécanique hamiltonienne
Modèle:AlEn mécanique hamiltonienne la variable [16] est remplacée par la variable appelée « moment conjugué » correspondant aux composantes Modèle:Nobr » appelées « moments conjugués » ou encore, quand les coordonnées correspondent à des coordonnées cartésiennes, « impulsions »[17] s'identifiant, en repérage cartésien, à celles de la quantité de mouvement pour un mouvement réel le long de la trajectoire réellement suivie[18] c.-à-d. « en cartésien » ;
est la transformée de Legendre[19] du lagrangien
soit
Modèle:Aldans le cas où la variable correspond à un mouvement réel le long de la trajectoire réellement suivie permettant de remplacer par «» ou encore
Modèle:AlModèle:Transparent«»[22] soit
Modèle:AlModèle:Transparent«»[23] ;
Modèle:Alde la différentielle de l'hamiltonien avec utilisation des équations d'Euler-Lagrange[13]Modèle:,[8] on tire les équations canoniques de Hamilton[7] «» Modèle:Nobr l'établissement dans l'encart ci-dessous,
Modèle:Encart
Modèle:AlModèle:Transparentpuis on tire des équations canoniques de Hamilton[7], dans la mesure où correspond à un mouvement réel le long de la trajectoire réellement suivie[24] :
Modèle:AlModèle:Transparentla définition de la quantité de mouvement de la particule car « » d'où
Modèle:AlModèle:Transparentla réécriture des 1ères équations canoniques de Hamilton[7] «» «»,
Modèle:AlModèle:Transparentla relation fondamentale de la dynamique car « »[25] d'où
Modèle:AlModèle:Transparentla réécriture des 2èmes équations canoniques de Hamilton[7] «» «» et
Modèle:AlModèle:Transparentla conservation de l'énergie mécanique de la particule si son énergie potentielle ne dépend pas explicitement du temps[26]
Modèle:AlModèle:Transparent«» «» d'où
Modèle:AlModèle:Transparentla réécriture de la 3ème équation canonique de Hamilton[7] «».
Construction de l'opérateur linéaire « hamiltonien » d'une particule quantique massique non relativiste
Modèle:AlEn utilisant la forme de l'hamiltonien d'une particule non relativiste «
»[27] nous en déduisons
Modèle:AlModèle:Transparentl'« opérateur linéaire hamiltonien » d'une particule « quantique » massique non relativiste à partir des opérateurs linéaires « énergie cinétique non relativiste »[28] et « énergie Modèle:Nobr
Modèle:All'action de cet opérateur linéaire
sur la fonction d'onde qui décrit un état stationnaire de la particule « quantique » non relativiste pour lequel l'énergie mécanique est fixée
Modèle:AlModèle:Transparentdonnant toutes les valeurs possibles d'énergie mécanique de « la particule en état stationnaire de composante spatiale de fonction d'onde
Équation de Schrödinger applicable à une particule quantique massique non relativiste
Expression de l'équation de Schrödinger suivie par une particule quantique massique non relativiste
Modèle:AlL'équation de Schrödinger[32] permet de décrire l'évolution temporelle de la fonction d'onde de la particule « quantique » massique non relativiste selon
Recherche des états propres de l'opérateur linéaire « hamiltonien » à énergie potentielle ne dépendant pas explicitement du temps, équation de Schrödinger indépendante du temps
Modèle:AlIntroduction : Dans le cas où l'énergie potentielle de la particule « quantique » ne dépend pas explicitement du temps,
Modèle:AlModèle:Transparentla particule peut être dans un état stationnaire voir la note « 35 » plus haut dans ce chapitre et,
Modèle:AlModèle:Transparentdans l'hypothèse où cette possibilité devient réalité, « la fonction d'onde de la particule se met sous la forme d'un produit avec fonction Modèle:Nobr
Modèle:AlExposé : L'équation de Schrödinger[32] d'une particule « quantique » dans un état stationnaire de fonction d'onde associée « avec fonction réelle »[33]
Modèle:AlModèle:Transparentse réécrit «» dans laquelle
Modèle:AlModèle:Transparent«»[34] et
Modèle:AlModèle:Transparent«»[35] d'où, par report
Modèle:AlModèle:Transparent«» puis
Modèle:AlModèle:Transparentaprès simplification par , «» soit,
Modèle:AlModèle:Transparenten supposant non identiquement nulle et en divisant chaque membre par ,
Modèle:AlModèle:Transparent«» dans laquelle le 1er membre de l'équation étant une fonction de et
Modèle:AlModèle:Transparentle 2nd Modèle:Transparentune fonction de ,
Modèle:AlModèle:Transparentceci n'est possible que si la fonction commune à chaque membre est une fonction constante ;
Modèle:AlModèle:Transparentnotant cette fonction constante nous obtenons less deux équations suivantes
Modèle:AlModèle:Transparent«» ;
Modèle:AlModèle:Transparentla 1ère équation «» s'intègre en « avec une constante réelle d'intégration » d'où la partie temporelle de la fonction d'onde de la particule « quantique » dans un état stationnaire « avec une constante complexe d'intégration » ;
Modèle:AlModèle:Transparentla 2ème équation se réécrit, en multipliant chaque membre par , «» appelée
Modèle:AlModèle:Transparent« équation de Schrödinger[32] indépendante du temps » ou,
Modèle:AlModèle:Transparentà l'aide de l'« opérateur linéaire hamiltonien » «»[36],
Modèle:AlModèle:Transparent«» représentant
Modèle:AlModèle:Transparentl'équation de recherche des états propres de l'« opérateur linéaire hamiltonien ».
Modèle:AlConclusion : Dans le cas où l'énergie potentielle de la particule « quantique » ne dépend pas explicitement du temps, cette dernière peut être dans un état stationnaire avec une fonction d'onde sous la forme forme «» dans laquelle est une valeur propre de l'« opérateur linéaire hamiltonien » de la particule c.-à-d. telle que «», la partie spatiale «» de la fonction d'onde étant une fonction propre associée à la valeur propre ces valeurs propres de l'« opérateur linéaire hamiltonien » de la particule s'identifient aux valeurs possibles de l'énergie mécanique de cette dernière[37] ;
Modèle:AlModèle:Transparentpour un niveau d'énergie connu de la particule « quantique » dans un état stationnaire, la partie spatiale «» de la fonction d'onde de la particule est solution de l'« équation de Schrödinger[32] indépendante du temps » équation aux dérivées partielles linéaire du 2ndordre «».
Modèle:AlPrincipaux résultats : Les valeurs de l'énergie de la particule « quantique » dans un état stationnaire peuvent être discrètes ou continues et
Modèle:AlModèle:Transparentà une valeur d'énergie fixée il peut correspondre plusieurs composantes spatiales de la fonction d'onde on dit dans ce cas que le niveau d'énergie est « dégénéré » :
- Modèle:Transparentdans le cas où le spectre d'énergie propre est discret et « pour un niveau d'énergie propre non dégénéré quantification des niveaux d'énergie, usuellement pour lequel la partie spatiale de la fonction d'onde propre s'écrit » solution de l'équation de Schrödinger[32] indépendante du temps Modèle:Nobr », la fonction d'onde propre complète de la particule dans cet état stationnaire s'écrit « » ;
- Modèle:Transparentdans le cas où le spectre d'énergie propre est discret et pour un niveau d'énergie propre dégénéré le caractère « dégénéré » des niveaux d'énergie n'engendrant usuellement aucune modification sur leur quantification pour lequel les parties spatiales des fonctions d'onde propres s'écrivent la dégénérescence d'un niveau d'énergie entraînant l'intervention d'au moins un 2ème paramètre discret usuellement permettant de distinguer les parties spatiales des fonctions d'onde entre elles» solutions indépendantes les unes des autres de l'équation de Schrödinger[32] indépendante du temps « », la fonction d'onde propre complète de la particule dans cet état propre du niveau d'énergie dégénéré s'écrivant « », la fonction d'onde propre complète de la particule dans l'état stationnaire de niveau d'énergie dégénéré est alors une C.L.[38] de chaque fonction d'onde propre complète correspondant à l'état propre du niveau d'énergie dégénéré [39] soit
Expression de la fonction d'onde décrivant un état quelconque de la particule quantique massique non relativiste à énergie potentielle ne dépendant pas explicitement du temps en utilisant les fonctions propres de l'opérateur linéaire « hamiltonien »
Modèle:AlDans le cas d'un spectre discret d'énergie
propre
de l'« opérateur linéaire hamiltonien » d'une particule « quantique » non relativiste à énergie potentielle ne dépendant pas explicitement du temps
Modèle:AlModèle:Transparent
chaque niveau d'énergie
étant considéré comme pouvant être dégénéré[42]
Modèle:AlModèle:Transparentavec, pour fonctions d'onde
complètes de la particule dans les états
propres
correspondants «
Modèle:Nobr
Modèle:AlModèle:Transparentla fonction d'onde complète décrivant un état quelconque de la particule peut être décomposée sur tous ces états propres et on obtient l'expression suivante
« est l'amplitude de l'état décrit par dans l'état propre »[43],
« étant la probabilité de trouver l'énergie lors d'une mesure de l'énergie de la particule »[44].
Conséquence du confinement spatial d'un oscillateur harmonique unidimensionnel dans le cadre de la mécanique quantique, l'impossibilité théorique d'être dans un état d'immobilité : notion d'énergie minimale de l'oscillateur harmonique quantique
Présentation d'un oscillateur harmonique unidimensionnel quantique
Modèle:AlUn oscillateur harmonique unidimensionnel quantique est une particule « quantique » non relativiste de masse restant localisée au voisinage d'un point sur un axe et
Modèle:AlModèle:Transparentpossédant une énergie potentielle de forme parabolique
Modèle:AlModèle:Transparenttelle que l'« amplitude d'oscillations[45] devant un ordre de grandeur de la longueur d'onde de Modèle:Nobr
Modèle:Alon réalise une réduction canonique en posant «» correspondant à sa pulsation propre[45] d'où une réécriture de l'énergie potentielle «» et par suite
Modèle:AlModèle:Transparentde l'hamiltonien[46] «» dans lequel l'énergie cinétique non relativiste s'écrit « étant la grandeur conjuguée de [47]» soit, après report dans l'expression de l'hamiltonien[46]
Modèle:AlModèle:Transparent«».
Exemples d'oscillateurs harmoniques unidimensionnels quantiques
- vibrations des atomes dans un solide : si les atomes sont alignés suivant trois directions, il y a un oscillateur harmonique unidimensionnel sur chacune d'elles traduisant les vibrations entre atomes voisins Modèle:Nobr façon schématique de représenter les interactions entre atomes est de les supposer reliées par un ressort de longueur à vide égale à la distance séparant les atomes voisins à l'équilibre et à spires non jointives, la compression du ressort traduisant une force répulsive et son allongement une force attractive ; les atomes dans un solide vibrant dans l'infra-rouge, l'amplitude de vibration peut correspondre effectivement à un oscillateur harmonique unidimensionnel quantique[48] ;
- vibrations des atomes dans une molécule diatomique comme la molécule de chlorure d'hydrogène : le système étant écarté légèrement de sa position d'équilibre stable oscille pour retrouver cette dernière, comme, par exemple, dans une molécule diatomique de chlorure d'hydrogène dans laquelle on a éloigné modérément les atomes et ;
Modèle:AlCommentaires : dans les exemples ci-dessus on considère deux objets en interaction assimilable à l'action d'un ressort
Modèle:AlModèle:Transparentmais la définition d'un oscillateur harmonique unidimensionnel évoquée au chap. intitulé oscillateur harmonique de la leçon « Signaux physiques (PCSI) »
Modèle:AlModèle:Transparentconcerne un objet soumis à l'action d'un ressort ;
Modèle:AlModèle:Transparenton peut effectivement s'y ramener car
Modèle:AlModèle:Transparentl'étude d'un système de deux points matériels se réduit à l'étude du mouvement de son « C.D.I.[49] »[50] et
Modèle:AlModèle:Transparentà celle d'un autre point fictif « le mobile réduit »[51] dans le « référentiel barycentrique »[52],
Modèle:AlModèle:Transparentpoint de masse dite réduite «» dont le mouvement barycentrique s'identifie au mouvement relatif de l'objet par rapport à Modèle:Nobr s'il est soumis à la force que l'objet exerce sur l'objet [53] c.-à-d., dans le cas présent, à l'action du ressort
Modèle:AlModèle:Transparenton est ramené à l'étude d'un oscillateur harmonique unidimensionnel évoquée au chap. oscillateur harmonique de la leçon « Signaux physiques (PCSI) ».
En complément : équation de Schrödinger de l'oscillateur harmonique unidimensionnel quantique indépendante du temps
Modèle:AlÀ partir de l'expression de l'hamiltonien d'un oscillateur harmonique unidimensionnel classique[54] «»
Modèle:AlModèle:Transparentétablie dans le paragraphe « présentation d'un oscillateur harmonique unidimensionnel quantique » plus haut dans ce chapitre, nous en déduisons
Modèle:AlModèle:Transparentcelle de l'« opérateur linéaire hamiltonien »[55] de l'oscillateur harmonique unidimensionnel quantique «»[4] ou
Modèle:AlModèle:Transparent«» d'où,
Modèle:AlModèle:Transparentl'expression de l'équation de Schrödinger[32] indépendante du temps à laquelle satisfait cet oscillateur harmonique unidimensionnel quantique
Modèle:AlModèle:Transparent«» avec
Modèle:AlModèle:Transparent« la partie spatiale de la ou de l'une des fonction(s) d'onde de cet oscillateur d'énergie », ou encore,
Modèle:AlModèle:Transparent«» soit
Modèle:AlModèle:Transparentune équation différentielle linéaire homogène du 2ème ordre en sans terme du 1er ordre[56].
Utilisation du confinement spatial d'un oscillateur harmonique unidimensionnel quantique
Modèle:AlUn oscillateur harmonique unidimensionnel classique ayant une énergie potentielle parabolique reste « confinée spatialement au voisinage de l'origine de l'axe »[57] ;
Modèle:Alnous allons déduire de l'inégalité de Heisenberg[58] spatiale[59] l'impossibilité théorique que l'oscillateur reste à l'équilibre c.-à-d. soit dans un état quantique d'immobilité, en effet
- Modèle:All'hypothèse de l'oscillateur quantique restant à sa position d'équilibre supposerait d'une part son abscisse parfaitement déterminée c.-à-d. à incertitude quantique nulle soit et
- Modèle:AlModèle:Transparentd'autre part sa quantité de mouvement exactement fixée c.-à-d. à incertitude quantique nulle soit ,
- Modèle:Alor la simultanéité des deux est en contradiction avec l'inégalité de Heisenberg[58] spatiale c.-à-d. en contradiction avec «»
- Modèle:AlModèle:Transparentd'où l'impossibilité théorique que l'oscillateur harmonique unidimensionnel quantique soit à l'équilibre ;
Modèle:Alles valeurs d'énergies propres de l'oscillateur harmonique unidimensionnel quantique étant a priori [60], l'impossibilité d'un état quantique d'immobilité à l'équilibrel'interdiction d'une valeur nulle Modèle:Nobr effet, pour que l'oscillateur harmonique unidimensionnel quantique ait une valeur nulle d'énergie il faudrait qu'il soit dans un état où simultanément et , ceci correspondant aussi à un état où simultanément et c.-à-d. un état quantique d'immobilité à l'équilibre, état interdit par inégalité de Heisenberg[58] spatiale[59].
Ordre de grandeur de l'énergie minimale de l'oscillateur harmonique unidimensionnel quantique
Modèle:AlToujours en utilisant l'inégalité de Heisenberg[58] spatiale[59] on se propose de déterminer un ordre de grandeur de l'énergie minimale de l'oscillateur harmonique unidimensionnel quantique c.-à-d.
Modèle:AlModèle:Transparentl'énergie de son état fondamental ;
Modèle:AlModèle:Transparentpour cela on détermine les propriétés ci-dessous[61] :
- oscillateur invariant par symétrie centrale de centre énergie potentielle paire valeur moyenne de sa position[45] «» soit une même probabilité[62] d'avoir la valeur et ;
compte-tenu du lien[45] entre et [63], la valeur moyenne de sa quantité de mouvement est aussi «»[64] correspondant à une même probabilité[62] d'avoir la valeur et ; - l'écart quadratique moyen sur les valeurs[45] de est donc «»[65]Modèle:,[66] ainsi que
Modèle:AlModèle:Transparentcelui sur les valeurs[45] de défini par «»[65]Modèle:,[66],
Modèle:Transparentces valeurs[62] « et » étant respectivement l'incertitude « quantique »[67] sur la position et la quantité de mouvement ; - l'énergie de l'oscillateur à valeur fixée[45] s'identifie à sa valeur moyenne [62] soit «»[65] ou encore, avec ,
Modèle:AlModèle:Transparentla valeur d'énergie suivante «»[65] ; - l'inégalité de Heisenberg[58] spatiale[59] liant les deux incertitudes « quantiques »[67] selon «» pour une incertitude « quantique »[67] sur la position fixée égale à ,
Modèle:AlModèle:Transparentune valeur minimale de l'incertitude « quantique »[67] sur sa quantité de mouvement
Modèle:AlModèle:Transparent«» soit,
Modèle:AlModèle:Transparenten reportant dans l'expression de l'énergie ci-dessus « Modèle:Nobr
Modèle:AlModèle:Transparentl'expression « optimale »[68] de l'énergie exprimée uniquement en fonction de l'incertitude « quantique »[67] sur la position «»
Modèle:AlModèle:Transparent«» ; - on cherche alors la valeur d'incertitude « quantique »[67] sur la position rendant minimale l'expression optimale de l'énergie , valeur notée «»,
Modèle:AlModèle:Transparent « Modèle:Nobr
Modèle:AlModèle:Transparentavec «» dont
Modèle:AlModèle:Transparentl'annulation donne «»[69] ; - la valeur minimale de l'expression optimale de l'énergie vaut donc «» soit finalement « ».
Modèle:AlConclusion : par utilisation de l'inégalité de Heisenberg[58] spatiale[59] on a obtenu un ordre de grandeur de l'énergie minimale d'un oscillateur harmonique unidimensionnel quantique «»,
Modèle:AlModèle:Transparentpour établir toutes les valeurs d'énergies possibles d'un tel oscillateur, la meilleure méthode est celle de Dirac[70] signalée dans la note « 62 » plus haut dans ce chapitre, en particulier
Modèle:AlModèle:Transparenton y établit celle de son énergie minimale, appelée « énergie du point zéro » c.-à-d. l'énergie de l'état Modèle:Nobr
Modèle:AlModèle:Transparentqui vaut effectivement «» ;
Modèle:AlModèle:Transparentce résultat n'est pas uniquement théorique, il explique entre autres, le fait que l'isotope de l'hélium «» reste liquide aux températures proches de [71].
Quantification (admise) de l'énergie d'un oscillateur harmonique unidimensionnel quantique
Spectre des niveaux d'énergie d'un oscillateur harmonique unidimensionnel quantique
Modèle:AlNous avons déjà dit que la méthode de Dirac[70] signalée dans la note « 62 » plus haut dans ce chapitre permet d'établir[72] toutes les valeurs d'énergies possibles d'un tel oscillateur ; on obtient
ou encore, à l'aide de la « fréquence propre de l'oscillateur »,
le spectre discret de niveaux d'énergie «»[74].
En complément : composante spatiale de la « fonction d'onde de l'état fondamental » d'un oscillateur harmonique unidimensionnel quantique

Modèle:AlÀ l'« énergie de l'état fondamental » correspond une “ seule ”[75] composante spatiale de fonction d'onde choisie Modèle:Nobr
Modèle:AlModèle:Transparent«»[76] dont le diagramme en fonction de est représenté ci-contre étant une unité de longueur arbitraire et une valeur particulière, homogène à , pouvant être quelconque et choisie égale à pour le tracé :
Modèle:Alon peut vérifier que cette composante est normalisée en évaluant la probabilité de l'état fondamental sur tout l'espace « »[77]Modèle:,[78] donnant lors son évaluation, en utilisant l'intégrale de Gauss[79] Modèle:Nobr », le résultat attendu dans le cas d'une normalisation «»[80].
En complément : composante spatiale de la « fonction d'onde de l'état correspondant au niveau n » d'un oscillateur harmonique unidimensionnel quantique
Modèle:AlÀ l'« énergie de l'état du niveau à savoir » correspond une “ seule ”[81] composante spatiale de fonction d'onde choisie réelle[82] égale à
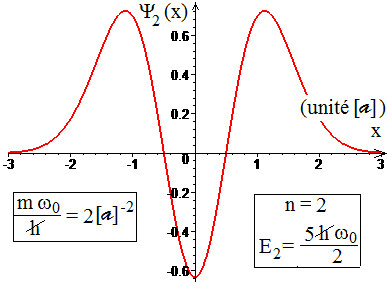
Modèle:AlModèle:Transparent« »[83]Modèle:,[84] dont les diagrammes de , de et de en fonction de sont représentés ci-dessous étant une unité de longueur arbitraire et une valeur particulière, homogène à , pouvant être quelconque et choisie égale à 2 pour le tracé :
-
Diagramme de la fonction d'onde de l'état de niveau d'énergie d'un oscillateur harmonique unidimensionnel quantique en fonction du paramètre de position
-
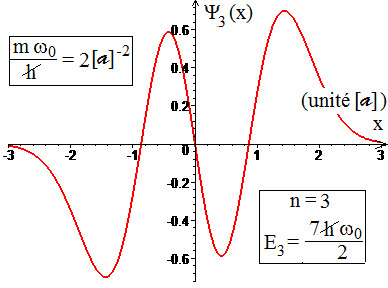
Diagramme de la fonction d'onde de l'état de niveau d'énergie d'un oscillateur harmonique unidimensionnel quantique en fonction du paramètre de position
-
Diagramme de la fonction d'onde de l'état de niveau d'énergie d'un oscillateur harmonique unidimensionnel quantique en fonction du paramètre de position
En complément : allure des diagrammes de densité linéique de probabilité de présence dans l'« état correspondant au niveau n » d'un oscillateur harmonique unidimensionnel quantique
Modèle:AlLa densité « linéique »[85] de probabilité de présence est liée à la composante spatiale de la fonction d'onde par «»[78] ;
Modèle:Alci-dessous de la gauche vers la droite les tracés, avec les mêmes conventions que précédemment, des diagrammes de :
- la densité linéique de probabilité de présence dans l'état fondamental «»[78] et
- la densité linéique de probabilité de présence dans l'état du 1er niveau excité «»[78],
-
Diagramme de la densité linéique de probabilité de présence de l'état fondamental d'un oscillateur harmonique unidimensionnel quantique en fonction du paramètre de position
-
Diagramme de la densité linéique de probabilité de présence de l'état de niveau d'énergie d'un oscillateur harmonique unidimensionnel quantique en fonction du paramètre de position
Modèle:Alpuis ci-dessous de la gauche vers la droite les tracés, avec les mêmes conventions que précédemment, des diagrammes de :
- la densité linéique de probabilité de présence dans l'état du 2ème niveau excité «»[78],
- la densité linéique de probabilité de présence dans l'état du 3ème niveau excité «»[78]
-
Diagramme de la densité linéique de probabilité de présence de l'état de niveau d'énergie d'un oscillateur harmonique unidimensionnel quantique en fonction du paramètre de position
-
Diagramme de la densité linéique de probabilité de présence de l'état de niveau d'énergie d'un oscillateur harmonique unidimensionnel quantique en fonction du paramètre de position
Modèle:AlRemarques : on constate que « la densité linéique de probabilité de présence est grossièrement maximale pour », ceci étant d'autant mieux vérifié que est grand [86], « cette valeur remplaçant l'amplitude des oscillations de l'oscillateur harmonique unidimensionnel classique »[87] ;
Modèle:AlModèle:Transparenton pourrait vérifier que n'est pas fonction propre de l'opérateur linéaire « quantité de mouvement » car [88].
-
Diagramme de la fonction d'onde de l'état de niveau d'énergie d'un oscillateur harmonique unidimensionnel quantique en fonction du paramètre de position
-
Diagramme de la densité linéique de probabilité de présence de l'état de niveau d'énergie d'un oscillateur harmonique unidimensionnel quantique en fonction du paramètre de position
Notes et références
- ↑ On peut donc affirmer que n'importe quelle valeur est valeur propre de l'opérateur linéaire « énergie potentielle » pour n'importe quelle fonction d'onde décrivant l'état de la particule « quantique », étant alors la fonction propre associée à la valeur propre .
- ↑ L'énergie cinétique d'une particule traduit la « réserve cinétique » de cette particule en intensité contrairement à la quantité de mouvement qui donne des informations sur la direction et le sens Modèle:Nobr le paragraphe « définition de l'énergie cinétique d'un point matériel dans le référentiel d'étude à partir des grandeurs d'inertie et cinétique précédemment introduite du point (cinétique newtonienne) » du chap. de la leçon « Mécanique 1 (PCSI) ».
- ↑ On rappelle l'expression de l'opérateur linéaire « quantité de mouvement » «», l'indice signifiant que l'on dérive à constant voir le paragraphe « inuction de l'opérateur linéaire quantité de mouvement » du chap. de la leçon « Signaux physiques (PCSI) ».
- ↑ 4,0 4,1 4,2 4,3 4,4 et 4,5 L'opérateur linéaire «» définissant l'opérateur linéaire du 2ème ordre « laplacien » noté voir le paragraphe « champ scalaire laplacien d'une fonction scalaire de l'espace » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » ;
Modèle:Alen repérage cartésien le laplacien s'écrit «» voir le paragraphe « expression du laplacien d'une fonction scalaire de l'espace en cartésien » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ». - ↑ Action qui revient à prendre le laplacien de la fonction d'onde à un facteur multiplicatif près.
- ↑ Les valeurs d'énergie cinétique non relativiste sont donc les valeurs propres de l'opérateur linéaire « énergie cinétique non relativiste », les fonctions d'onde particulières décrivant l'état de la particule étant les fonctions propres associées.
- ↑ 7,0 7,1 7,2 7,3 7,4 et 7,5 William Rowan Hamilton (1805 - 1865) mathématicien, physicien et astronome irlandais connu pour sa découverte des quaternions mais a contribué aussi au développement de l'optique, de la dynamique et de l'algèbre ; il est aussi connu comme l'inventeur de la mécanique hamiltonienne fondée sur un principe variationnel, le principe de moindre action.
- ↑ 8,0 8,1 8,2 et 8,3 Joseph-Louis Lagrange (1736 -1803) mathématicien, mécanicien et astronome français d'origine italienne, ayant jeté les bases du calcul variationnel à l'âge de ans qui lui permirent d'achever ans plus tard la construction de la mécanique analytique connue actuellement sous le nom de mécanique lagrangienne ; on lui doit beaucoup d'autres travaux dans le domaine des mathématiques, celui de la mécanique mécanique des fluides et celui de l'astronomie problème des trois corps.
- ↑ La variable n'étant, pour l'instant, pas considérée comme la dérivée temporelle de la position il ne s'agit donc, pour l'instant, qu'une simple notation et non, a priori, la vitesse ; toutefois les deux variables et sont supposées être des fonctions indépendantes du temps , la 2ème variable devenant la dérivée temporelle de la 1ère c.-à-.d la vitesse pour un mouvement réel le long de la trajectoire réellement suivie.
- ↑ Dans laquelle est l'énergie potentielle de la particule, le 1er terme devenant son énergie cinétique dès lors que la variable est interprétée comme sa vitesse.
- ↑ Qu'on notera simplement, en absence d'ambiguïté, .
- ↑ C.-à-d. que l'« action » sur l'intervalle ne varie pas à l'ordre un lors d'une perturbation infinitésimale des variables et relativement à leur valeur correspondant à un mouvement réel le long de la trajectoire réellement suivie soit,
- pour la 1ère variable étant la perturbation infinitésimale de la 1ère variable et
- pour la 2ème étant la perturbation infinitésimale de la 2ème variable, dérivée temporelle de de façon à ce que la 2ème variable devienne la vitesse si ,
- étant l'infiniment petit d'ordre un et une fonction vectorielle différentiable telle que assurant que la trajectoire réellement suivie passe par les points extrêmes définis par et , la vitesse en ces points étant alors définie par et .
- ↑ 13,0 13,1 et 13,2 Leonhard Euler (1707 - 1783) mathématicien et physicien suisse qui passa la plus grande partie de sa vie dans l'Empire russe et en Allemagne, surtout connu pour ses travaux en analyse mathématique ainsi qu'en mécanique des fluides, optique et astronomie, considéré comme l'un des plus grands et plus prolifiques mathématiciens de tous les temps ;
Modèle:Alen mathématiques il fit d'importantes découvertes dans des domaines aussi variés que le calcul infinitésimal et la théorie des graphes, il introduisit également une grande partie de la terminologie et de la notation des mathématiques modernes, en particulier pour l'analyse mathématique, comme la notion de fonction mathématique ; il est aussi connu pour ses travaux en mécanique, en dynamique des fluides, en optique et en astronomie. - ↑ Voir le paragraphe « composantes cartésiennes du gradient d'une fonction scalaire de l'espace » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ Voir le paragraphe « énergie potentielle d'un point matériel dans un champ de force conservative » du chap. de la leçon « Mécanique 1 (PCSI) ».
- ↑ Laquelle s'identifie à la dérivée temporelle de la position c.-à-d. à la vitesse pour un mouvement réel le long de la trajectoire réellement suivie.
- ↑ Dans le cadre de la mécanique analytique regroupant la mécanique lagrangienne et la mécanique hamiltonienne elles sont encore appelées, quand les coordonnées sont des coordonnées cartésiennes, « moments linéaires » pour souligner que ces variables ne sont pas associées à des coordonnées angulaires.
- ↑ En effet .
- ↑ Adrien-Marie Legendre (1752 - 1833) mathématicien français fit d’importantes contributions à la statistique, à la théorie des nombres, aux algèbres abstraites et à l'analyse en particulier sur les polynômes dits de Legendre mais une grande partie de ses travaux fut finalisée par d'autres.
- ↑ Il s'agit en fait de l'opposé de la transformée de Legendre défini dans l'article transformation de Legendre de wikipedia, la raison étant qu'il n'y a pas de convention de signe dans le choix de la définition, la convention choisie dans l'article précitée aurait donné et aurait été tout aussi licite.
- ↑ Avec cette convention de signe l'hamiltonien s'écrit encore «».
- ↑ On rappelle la définition du lagrangien dans laquelle on remplace par .
- ↑ L'hamiltonien s'identifie donc à l'énergie mécanique, somme de l'énergie cinétique et de l'énergie potentielle si toutefois il représente un mouvement réel le long de la trajectoire réellement Modèle:Nobr
- ↑ Ce qui est le cas car, pour les établir, on a utilisé les équations d'Euler-Lagrange qui ont été déduites de l'application du principe de moindre action.
- ↑ En utilisant le lien entre la force appliquée à la particule et l'énergie potentielle dont elle dérive «» voir les notes « 18 » et «19 » plus haut dans ce chapitre.
- ↑ C'est le cas le plus usuel, lequel nécessite que la force ne dépendant pas explicitement du temps soit conservative voir le paragraphe « 1ère définition d'une force conservative » du chap. de la leçon « Mécanique 1 (PCSI) ».
- ↑ Cette forme suppose que la particule a un mouvement réel sur la trajectoire réellement suivie c.-à-d. que son mouvement obéit au principe variationnel de la mécanique « le principe de moindre action » ce qui a pour conséquence les trois équations canoniques de Hamilton dont la 1ère rend le moment conjugué identique à la quantité de mouvement de la particule.
- ↑ 28,0 et 28,1 Voir le paragraphe « opérateur linéaire énergie cinétique non relativiste d'une particule quantique massique » plus haut dans ce chapitre.
- ↑ Erreur de référence : Balise
<ref>incorrecte : aucun texte n’a été fourni pour les références nomméesopérateur énergie potentielle - ↑ Pour qu'une particule non quantique ait une valeur constante de son hamiltonien, il est nécessaire que son énergie potentielle ne dépende pas explicitement du temps 3ème équation canonique de Hamilton, il s'en suit alors la conservation de l'énergie mécanique ;
Modèle:Aldu point de vue quantique, dans la mesure où l'énergie potentielle de la particule ne dépend pas du temps, la particule peut être dans un état stationnaire c.-à-d. que le module de la fonction d'onde qui modélise l'état considéré ne dépend pas non plus du temps la fonction d'onde peut alors être cherchée sous la forme du produit d'une composante spatiale et d'une composante temporelle de module unité dont l'argument dépend de l'état stationnaire considéré, la composante spatiale étant solution de l'équation de Schrödinger indépendante du temps voir le paragraphe « recherche des états propres de l'opérateur linéaire hamiltonien à énergie potentielle ne dépendant pas explicitement du temps, équation de Schrödinger indépendante du temps » plus loin dans ce chapitre, c.-à-d. «» ou «» la composante spatiale de la fonction d'onde associée à un état stationnaire est une fonction propre de l'« opérateur linéaire hamiltonien » associée à la valeur propre la constance de l'hamiltonien d'une particule non quantique et par suite la conservation de son énergie mécanique devient, pour une particule « quantique » dans un état stationnaire, le fait que ce dernier est un état propre de l'« opérateur linéaire hamiltonien », la valeur propre associée étant l'énergie de la particule énergie restant constante hors influence extérieure. - ↑ Dans la mesure où la particule est dans un état stationnaire, ses valeurs d'énergie mécanique non relativiste sont donc les valeurs propres de l'« opérateur linéaire hamiltonien », les fonctions d'onde décrivant l'état stationnaire de la particule étant les fonctions propres associées.
- ↑ 32,0 32,1 32,2 32,3 32,4 32,5 et 32,6 Erwin Rudolf Josef Alexander Schrödinger (1887 - 1961) physicien, philosophe et théoricien scientifique autrichien est à l'origine du développement d'un des formalismes théoriques de la mécanique quantique connu sous le nom de mécanique ondulatoire ; la formulation de l'équation d'onde connue sous le nom d'équation de Schrödinger lui a valu de partager le prix Nobel de physique en avec Paul Dirac lequel a été honoré pour la découverte de formes nouvelles et utiles de la théorie atomique ; on doit encore à Erwin Schrödinger l'expérience de pensée proposée à Albert Einstein en et connue sous le nom chat de Schrödinger.
Modèle:AlPaul Adrien Maurice Dirac (1902 - 1984) physicien et mathématicien britannique : voir la note « 77 » plus bas dans ce chapitre pour plus de détails.
Modèle:AlAlbert Einstein (1879 - 1955), physicien théoricien d'origine allemande, devenu apatride en puis suisse en ; on lui doit la théorie de la relativité restreinte publiée en , la relativité générale en ainsi que bien d'autres avancées dans le domaine de la mécanique quantique et la cosmologie ; il a reçu le prix Nobel de physique en pour son explication de l'effet photoélectrique. - ↑ Erreur de référence : Balise
<ref>incorrecte : aucun texte n’a été fourni pour les références nomméesforme de fonction d'onde associée à un état stationnaire - ↑ restant constant lors de la prise de laplacien à figé.
- ↑ restant constant lors de la dérivation partielle par rapport au temps à figé voir le paragraphe « définition des dérivées partielles » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) », la généralisation à plus de deux variables indépendantes ne présentant aucune difficulté apparente.
- ↑ Voir le paragraphe « construction de l'opérateur linéaire hamiltonien d'une particule quantique non relativiste » plus haut dans ce chapitre.
- ↑ Revoir la note « 36 » plus haut dans ce chapitre.
- ↑ Combinaison Linéaire.
- ↑ L'ensemble des étant le degré de dégénérescence du niveau d'énergie formant une base de l'espace propre associé au niveau d'énergie .
- ↑ Il s'agit d'une façon raccourcie de dire « amplitude de l'état stationnaire décrit par la fonction d'onde sur l'état propre décrit par » ;
Modèle:Alchaque scalaire est l'analogue de la composante sur un vecteur de base d'un vecteur d'un espace à dimensions, étant le degré de dégénérescence du niveau d'énergie considéré. - ↑ Il s'agit d'une façon raccourcie de dire « probabilité de l'état propre décrit par la fonction d'onde dans l'état de la particule décrit par la fonction d'onde Modèle:Nobr
Modèle:Alpour des probabilités normalisées quand cela est possible la condition de normalisation s'écrit «» certitude que la particule étudiée est dans le niveau d'énergie . - ↑ S'il est dégénéré, chaque état propre est indexé par un paramètre et s'il ne l'est pas ne prend que la valeur .
- ↑ Il s'agit d'une façon raccourcie de dire « amplitude de l'état décrit par la fonction d'onde sur l'état propre décrit par » ;
Modèle:Alchaque scalaire est l'analogue de la composante d'un vecteur quelconque sur un vecteur de base du sous-espace à dimensions étant le degré de dégénérescence du niveau d'énergie . - ↑ Pour des probabilités normalisées quand cela est possible la condition de normalisation s'écrit «» certitude de trouver une valeur lors de la mesure de l'énergie de la particule dans l'état décrit par la fonction d'onde .
- ↑ 45,0 45,1 45,2 45,3 45,4 45,5 et 45,6 Au sens classique.
- ↑ 46,0 et 46,1 Qui s'identifie à l'énergie mécanique dans le cadre classique d'une particule.
- ↑ À signification de quantité de mouvement pour une particule classique.
- ↑ En effet nous avons précisé dans la note « 51 » plus haut dans ce chapitre que la condition pour que l'oscillateur soit quantique est que l'amplitude de vibrations satisfasse Modèle:Nobr ou, avec dans laquelle est la fréquence de vibration, «» soit, avec et , « », les atomes étant séparés de quelques les uns des autres, l'amplitude de vibration devrait être à une fraction de cette distance tout à fait envisageable.
- ↑ Centre D'Inertie.
- ↑ Notion introduite au paragraphe « centre d'inertie d'un système (discret) fermé de points matériels » du chap. de la leçon « Mécanique 1 (PCSI) » définissant le centre d'inertie comme le « barycentre des positions des points affectés de leur masse comme cœfficient » voir le paragraphe « définition du barycentre d'un système de n points pondérés » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ N'est pas au programme de physique de P.C.S.I. mais c'est pourtant fondamental dans l'étude des systèmes de deux points, lesquels sont au programme voir le paragraphe « notion de mobile réduit » du chap. de la leçon « Mécanique des systèmes de points ».
- ↑ Référentiel en translation par rapport au référentiel d'étude et tel que le C.D.I. centre d'inertie y soit immobile voir le paragraphe « définition (du référentiel barycentrique d'un système de deux points matériels) » du chap. de la leçon « Mécanique des systèmes de points ».
- ↑ Voir le paragraphe « recherche de la force à imposer au mobile réduit pour que son mouvement barycentrique s'identifie au mouvement relatif de M2 par rapport à M1 et conséquence » du chap. de la leçon « Mécanique des systèmes de points ».
- ↑ « Classique » au sens de « non quantique » et « non relativiste ».
- ↑ Voir le paragraphe « construction de l'opérateur linéaire hamiltonien d'une particule quantique massique non relativiste » plus haut dans ce chapitre.
- ↑ Cette équation n'étant pas à cœfficients constants, sa résolution ne relève pas de la recherche de solutions de forme exponentielle et par conséquent de la résolution de l'équation caractéristique correspondante ;
Modèle:Alde toute façon l'équation de Schrödinger étant un complément, nous ne chercherons pas à la résoudre, la résolution mathématique du type d'équation différentielle suivie par l'oscillateur harmonique unidimensionnel quantique serait d'ailleurs, hors de portée au niveau de la présentation, car nécessitant de connaître les développements de fonctions en séries entières, elle ne présente toutefois pas de difficultés majeures mais conduit à des calculs un peu laborieux ;
Modèle:Ald'autre part la méthode de résolution par développement en séries entières étant peu explicite physiquement, une autre approche, impulsée par Paul Adrien Maurice Dirac, lui est préférable, elle fournit les valeurs propres de l'« opérateur linéaire hamiltonien » , c.-à-d. les valeurs d'énergie sans résoudre explicitement l'équation différentielle.
Modèle:AlPaul Adrien Maurice Dirac (1902 - 1984) physicien et mathématicien britannique : voir la note « 77 » plus bas dans ce chapitre pour plus de détails.
Modèle:AlErwin Rudolf Josef Alexander Schrödinger (1887 - 1961) physicien, philosophe et théoricien scientifique autrichien : voir la note « 37 » plus haut dans ce chapitre pour plus de détails. - ↑ Une 2ème définition d'un oscillateur harmonique unidimensionnel classique c.-à-d. « objet piégé dans un puits d'énergie potentielle parabolique » est justifiée dans le paragraphe « rappel de l'intégrale 1ère énergétique de l'oscillateur harmonique à une dimension constitué d'un pendule élastique horizontal non amorti (P.E.H.N.A.) » du chap. de la leçon « Mécanique 1 (PCSI) » et
Modèle:Alla propriété de « confinement spatial » d'un oscillateur harmonique unidimensionnel classique établie dans le paragraphe « présence de deux murs d'énergie potentielle : trajectoire du point matériel cinétiquement bornée » du même chap. de la même leçon « Mécanique 1 (PCSI) ». - ↑ 58,0 58,1 58,2 58,3 58,4 et 58,5 Werner Heisenberg (1901 - 1976) physicien allemand, l'un des fondateurs de la mécanique quantique, a obtenu le prix Nobel de physique en pour la création d'une forme de mécanique quantique connue sous le nom de mécanique matricielle, dont l’application a mené, entre autres, à la découverte des variétés allotropiques de l'hydrogène le dihydrogène existe sous deux formes allotropiques « ortho » où les spins sont parallèles et « para » où ils sont antiparallèles, le dihydrogène ortho étant présent à à température élevée et sa proportion diminuant quand sa température diminue.
- ↑ 59,0 59,1 59,2 59,3 et 59,4 Voir le paragraphe « induction de l'inégalité de Heisenberg spatiale à partir de la relation de diffraction appliquée à un photon » du chap. de la leçon « Signaux physiques (PCSI) ».
- ↑ Comme c'est le cas pour un oscillateur harmonique unidimensionnel classique, l'énergie étant la somme de l'énergie cinétique et de l'énergie potentielle toutes deux positives ou nulles.
- ↑ Pour les deux 1ères en restant dans le cadre de la mécanique classique puis en admettant leur validité dans le cadre de la mécanique ondulatoire.
- ↑ 62,0 62,1 62,2 et 62,3 Au sens quantique.
- ↑ On rappelle qu'en cinétique newtonienne .
- ↑ L'invariance du mouvement par symétrie centrale entraînant .
- ↑ 65,0 65,1 65,2 et 65,3 La notation représentation la valeur moyenne pour une série de valeurs de la grandeur , notation équivalente à .
- ↑ 66,0 et 66,1 Voir le paragraphe « incertitudes théoriques sur la quantité de mouvement et sur la position transversales du photon lors de l'expériences de diffraction appliquée à un photon » du chap. de la leçon Signaux physiques (PCSI) », la généralisation à n'importe quelle particule quantique ne faisant sans restriction.
- ↑ 67,0 67,1 67,2 67,3 67,4 et 67,5 On parle d'incertitude « quantique » car c'est une incertitude théorique contenue dans les principes de la mécanique quantique, et non une incertitude « expérimentale ».
- ↑ Au sens où l'incertitude quantique sur la quantité de mouvement est la plus faible, du point de vue théorique, relativement à l'incertitude quantique sur la position.
- ↑ L'expression optimale de l'énergie «» est effectivement minimale pour cette valeur «» car
Modèle:AlModèle:Transparentla dérivée calculée «» est- pour les valeurs de à elle tend vers quand donc y est et
- pour les valeurs de à elle tend vers quand donc y est .
- ↑ 70,0 et 70,1 Paul Adrien Maurice Dirac (1902 - 1984) physicien et mathématicien britannique, colauréat du prix Nobel de physique en , on lui doit des avancées cruciales dans le domaine de la mécanique statistique et de la physique quantique des atomes, il démontra l'équivalence physique entre la mécanique ondulatoire de Schrödinger et la mécanique matricielle de Heisenberg, deux présentations de la même mécanique quantique et enfin, pour les besoins du formalisme quantique, il inventa la notion, sans fondement mathématique précis, connue de nos jours sous le nom de distribution de Dirac et dont la description rigoureuse fut établie par le mathématicien français Laurent Schwartz dans sa théorie des distributions ; Paul Dirac fut colauréat du prix Nobel de Physique en pour la découverte de formes nouvelles et utiles de la théorie atomique, l'autre moitié du prix Nobel étant décernée à Erwin Schrödinger pour la formulation de l'équation d'onde dite de Schrödinger.
Modèle:AlErwin Rudolf Josef Alexander Schrödinger (1887 - 1961) physicien, philosophe et théoricien scientifique autrichien : voir la note « 37 » plus haut dans ce chapitre pour plus de détails.
Modèle:AlWerner Heisenberg (1901 - 1976) physicien allemand, l'un des fondateurs de la mécanique quantique : voir la note « 64 » plus haut dans ce chapitre pour plus de détails.
Modèle:AlLaurent Schwartz (1915 - 2002) mathématicien français, ayant été le 1er français à obtenir la médaille Fields équivalent du prix Nobel en mathématiques en pour ses travaux sur la théorie des distributions sorte de prolongement des fonctions dans des domaines avec discontinuité . - ↑ Au voisinage de une approche classique conduirait à une énergie nulle avec absence de mouvements relatifs entre molécules et par suite une impossibilité de phase liquide à l'absence de mouvements relatifs entre molécules ou atomes ne s'observant que dans une phase solide, ce qui n'est pas ce qu'on observe, d'où la nécessité de faire une approche quantique conduisant à une « énergie non nulle quand l'hélium s'approche de » et permettant l'explication de la phase liquide de ce dernier aux températures voisines de .
- ↑ Néanmoins nous ne le ferons pas, bien que la construction du spectre des valeurs propres de l'énergie soit sans difficultés majeures mais toutefois un peu délicate pour les raisons suivantes :
- d'une part leur établissement n'est pas au programme de physique de PCSI seul le résultat admis l'étant et
- d'autre part c'est un peu long à détailler ;
Modèle:AlModèle:Transparentles sous-paragraphes « introduction d'opérateurs sans dimension » étant noté dans ce Modèle:Nobr
Modèle:AlModèle:Transparent« opérateurs d'échelle » où est utilisée la notion d'opérateur hermitique ou hermitien et donc non-hermitique ou non-hermitien pour cela voir aussi la définition de l'opérateur adjoint d'un opérateur dans ce sous-paragraphe ainsi que la notion de commutateur de deux opérateurs linéaires Modèle:Nobr la note « 41 » du chap. de la leçon « Signaux physiques (PCSI) » et enfin le dernier sous-paragraphe
Modèle:AlModèle:Transparent« calcul des valeurs propres ».
Modèle:AlCharles Hermite (1822 - 1901) mathématicien français connu pour ses travaux sur la théorie des nombres, les formes quadratiques, les polynômes othogonaux, les fonctions elliptiques et les équations différentielles, il fut aussi l'un des 1ers à utiliser les matrices ; le qualificatif « hermitien » donné à certaines entités mathématiques l'a été pour lui rendre hommage. - ↑ Il y a donc quantification de l'énergie, celle-ci dépendant du nombre quantique entier naturel, le quantum étant .
- ↑ Le quantum d'énergie se réécrit donc .
- ↑ L'état fondamental n'est donc pas dégénéré.
- ↑ Là encore, bien que la résolution de l'équation de Schrödinger indépendante du temps de l'oscillateur harmonique unidimensionnel quantique dans son état fondamental ne présente pas de difficultés majeures tout en étant un peu délicate nous ne la présenterons pas pour les raisons suivantes :
- d'une part la résolution n'est pas au programme de physique de PCSI même le résultat ne l'est pas, bien qu'intéressant à observer et
- d'autre part c'est un peu long à détailler ;
Modèle:AlModèle:Transparentle sous-paragraphe « non-dégénrescence de l'état fondamental » nécessitant l'utilisation des « opérateurs d'échelle » où est utilisée la notion d'opérateur hermitique ou hermitien et donc non-hermitique ou non-hermitien pour cela voir aussi la définition de l'opérateur adjoint d'un opérateur dans ce sous-paragraphe ainsi que la notion de commutateur de deux opérateurs linéaires Modèle:Nobr la note « 41 » du chap. de la leçon « Signaux physiques (PCSI) ».
Modèle:AlErwin Rudolf Josef Alexander Schrödinger (1887 - 1961) physicien, philosophe et théoricien scientifique autrichien : voir la note « 37 » plus haut dans ce chapitre pour plus de détails.
Modèle:AlCharles Hermite (1822 - 1901) mathématicien français : voir la note « 79 » plus haut dans ce chapitre pour plus de détails. - ↑ Il s'agit d'une intégrale généralisée voir le paragraphe « intégrale généralisée sur un ouvert dont au moins une des bornes est infinie » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » pour laquelle théoriquement on calcule l'intégrale sur et on vérifie qu'elle admet une limite finie quand , mais la fonction à intégrer ici n'admettant pas de primitives parmi les fonctions usuelles, cette façon de vérifier la convergence ne pourra être faite toutefois elle converge ;
Modèle:Alon utilise alors le résultat de l'intégrale «» connue sous le nom d'« intégrale de Gauss », très utilisée en statistique et probabilité.
Modèle:AlCarl Friedrich Gauss (1777 - 1855), mathématicien, astronome et physicien allemand, est considéré comme l'un des plus grands mathématiciens de tous les temps il fut surnommé « le prince des mathématiciens » : voir la note « 87 » plus bas dans ce chapitre pour plus de détails. - ↑ 78,0 78,1 78,2 78,3 78,4 et 78,5 Voir le paragraphe « notion de fonction d'onde de matière (densité volumique de probabilité de présence) » du chap. de la leçon « Signaux physiques (PCSI) », la densité volumique devant être remplacée par densité linéique dans le cas d'un objet à une dimension.
- ↑ Carl Friedrich Gauss (1777 - 1855), mathématicien, astronome et physicien allemand, est considéré comme l'un des plus grands mathématiciens de tous les temps il fut surnommé « le prince des mathématiciens », on lui doit d'importantes contributions dans les trois domaines « mathématiques, astronomie et physique » :
Modèle:Alen , Gauss, à l'âge de dix-neuf ans, caractérisa presque complètement tous les polygones réguliers constructibles à la règle et au compas et il demanda par la suite qu'un heptadécagone Modèle:Nobr régulier de côtés soit gravé sur son tombeau ; bien d'autres découvertes de mathématiques lui sont dues dont, en particulier, en la 1ère démonstration de la loi de réciprocité quadratique conjecturée par Euler en un nombre premier est congru à un carré de nombre entier modulo un autre nombre premier, par exemple ou ou encore de même que Leonhard Euler (1707 - 1783) mathématicien et physicien suisse qui passa la plus grande partie de sa vie dans l'Empire russe et en Allemagne : voir la note « 13 » plus haut dans ce chapitre pour plus de détails ;
Modèle:Aldans le domaine de l'astronomie Gauss publia un travail très important sur le mouvement des corps célestes contenant le développement de la méthode des moindres carrés ; auparavant, en , il développa une nouvelle méthode de calcul lui permettant de prédire où doit se trouver Cérès une planète naine de la ceinture des astéroïdes entre Mars et Jupiter ;
Modèle:Aldans le domaine de la physique il est l'auteur de deux des quatre équations de Maxwell gérant l'électromagnétisme James Clerk Maxwell (1831 - 1879) physicien et mathématicien écossais, principalement connu pour ses équations unifiant l'électricité, le magnétisme et l'induction ainsi que pour l'établissement du caractère électromagnétique des ondes lumineuses, mais aussi pour sa distribution des vitesses utilisée dans une description statistique de la théorie cinétique des gaz ; le tire-bouchon fictif permettant de déterminer l'orientation à droite d'un espace tridimensionnel ou le caractère direct d'un triplet de vecteurs a été baptisé « tire-bouchon de Maxwell » en son honneur ;
Modèle:Alcertaines des contributions de Gauss n'ont été mises à jour qu'à titre posthume, à la fin du XIXème siècle, Gauss n'ayant publié qu'une partie de ses découvertes. - ↑ En effet .
- ↑ L'état de niveau n'est donc pas dégénéré.
- ↑ Erreur de référence : Balise
<ref>incorrecte : aucun texte n’a été fourni pour les références nomméeschoisie réelle - ↑ Là encore, bien que la résolution de l'équation de Schrödinger indépendante du temps de l'oscillateur harmonique unidimensionnel quantique dans l'état de niveau ne présente pas de difficultés majeures tout en étant un peu délicate nous ne la présenterons pas pour les raisons suivantes :
- d'une part la résolution n'est pas au programme de physique de PCSI même le résultat ne l'est pas, bien qu'intéressant à observer et
- d'autre part c'est un peu long à détailler ;
Modèle:AlModèle:Transparentle sous-paragraphe « états propres de l'opérateur N » nécessitant l'utilisation des « opérateurs d'échelle » où est utilisée la notion d'opérateur hermitique ou hermitien et donc non-hermitique ou non-hermitien pour cela voir aussi la définition de l'opérateur adjoint d'un opérateur dans ce sous-paragraphe ainsi que la notion de commutateur de deux opérateurs linéaires Modèle:Nobr la note « 41 » du chap. de la leçon « Signaux physiques (PCSI) ».
Modèle:AlErwin Rudolf Josef Alexander Schrödinger (1887 - 1961) physicien, philosophe et théoricien scientifique autrichien : voir la note « 37 » plus haut dans ce chapitre pour plus de détails.
Modèle:AlCharles Hermite (1822 - 1901) mathématicien français : voir la note « 79 » plus haut dans ce chapitre pour plus de détails. - ↑ Pratiquement est obtenue, à un facteur multiplicatif près, en appliquant fois successivement l'opérateur à la composante spatiale de la fonction d'onde de l'état fondamental , le facteur multiplicatif arbitraire de pouvant être déterminé par normalisation de la fonction d'onde.
- ↑ Remplace la densité volumique pour un objet à une dimension.
- ↑ Voir les tracés ci-après de et de le cas a été choisi comme suffisamment grand pour vérifier la propriété énoncée sans toutefois l'être trop sachant que « plus est grand plus la durée nécessaire pour obtenir le tracé l'est ».
- ↑ En effet à cet endroit, l'oscillateur harmonique unidimensionnel classique ayant une vitesse minimale en fait nulle pour un oscillateur purement classique c'est l'endroit où la probabilité de le trouver à un instant choisi au hasard est la plus grande ; c'est aussi l'endroit où sa quantité de mouvement est minimale en fait nulle si l'oscillateur est purement classique et sa longueur d'onde de de Broglie maximale en fait infinie si l'oscillateur est purement classique, donc l'endroit où les phénomènes quantiques seront les plus apparents, la condition d'inobservation sur l'amplitude de des phénomènes quantiques étant ayant un risque quasi nul d'être réalisée voir la note « 51 » plus haut dans ce chapitre.
Modèle:AlLouis Victor de Broglie (1892 - 1987) se prononce « Brogle » mathématicien et physicien français : voir la note « 51 » plus haut dans ce chapitre pour plus de détails. - ↑ La non proportionnalité de à assurant que n'est pas fonction propre de , s'il y avait eu proportionnalité, le cœfficient de proportionnalité aurait été la valeur propre correspondant à la fonction propre, on retrouve ainsi que la quantité de mouvement n'a pas de valeur fixée dans cet état.