Outils mathématiques pour la physique (PCSI)/Barycentre d'un système de points

Modèle:AlOn va se limiter au cadre de la géométrie élémentaire pour introduire la notion de barycentre d'un système de points $($avec son utilisation pratique en physique$)$.

Barycentre de deux points

Modèle:AlCette notion peut être introduite dès lors qu'on associe à chaque point une grandeur additive, non nulle caractérisant le point,
Modèle:AlModèle:Transparenton dit alors que les points sont « pondérés » par cette grandeur, celle-ci définissant le cœfficient affecté au point .

Définition du barycentre d'un système de deux points pondérés

Modèle:AlSoit le système de deux points pondérés $\{A(\alpha ),B(\beta )\}$, les cœfficients affectés aux points étant tous deux $\ne 0$, on appelle
Modèle:AlModèle:Transparentbarycentre de ce système de deux points pondérés le point $G$ tel que «$\alpha \overrightarrow{GA}+\beta \overrightarrow{GB}=\overrightarrow{0}$».

Modèle:AlCondition d'existence et d'unicité : Supposons l'existence du barycentre du système $\{A(\alpha ),B(\beta )\}$ et
Modèle:AlModèle:Transparentappliquons la relation de Chasles $\overrightarrow{GB}=$ $\overrightarrow{GA}+\overrightarrow{AB}$ que l'on reporte dans la définition de $G$ soit
Modèle:AlModèle:Transparent$\alpha \overrightarrow{GA}+\beta (\overrightarrow{GA}+\overrightarrow{AB})=\overrightarrow{0}$ d'où l'équation suivante $(\alpha +\beta )\overrightarrow{GA}=-\beta \overrightarrow{AB}$ ;
Modèle:AlModèle:Transparenton en déduit une C.N. d'existence du barycentre du système $\{A(\alpha ),B(\beta )\}$ qui est «$\alpha +\beta \ne 0$» et
Modèle:AlModèle:Transparentsous cette condition on obtient une solution unique «$\overrightarrow{GA}=-\frac{\beta }{\alpha +\beta }\overrightarrow{AB}$».
Modèle:AlModèle:TransparentConclusion : le barycentre du système $\{A(\alpha ),B(\beta )\}$ n'existe et est unique que si «$\alpha +\beta \ne 0$».

Modèle:AlRemarque : On peut prolonger la définition du barycentre du système $\{A(\alpha ),B(\beta )\}$ au cas où $\alpha +\beta =0$ à condition d'admettre que le barycentre puisse être un point à l'infini sur une direction, ainsi
Modèle:AlModèle:Transparentde $(\alpha +\beta )\overrightarrow{AG}=\beta \overrightarrow{AB}$ on déduit que « le barycentre du système $\{A(\alpha ),B(\beta )\}$ avec $\alpha +\beta =0$ est le point à l'infini de la direction $(AB)$» .

Vecteur position du barycentre du système de deux points pondérés

Modèle:Al$O$ étant un point quelconque de l'espace, on utilise la relation de Chasles pour réécrire $\left\{\begin{array}{c}\overrightarrow{GA}=\overrightarrow{OA}-\overrightarrow{OG}\\ \overrightarrow{GB}=\overrightarrow{OB}-\overrightarrow{OG}\end{array}\right\}$ que l'on reporte dans la définition du barycentre «$\alpha \overrightarrow{GA}+\beta \overrightarrow{GB}=\overrightarrow{0}$» $\Rightarrow$
Modèle:AlModèle:Transparent$\alpha [\overrightarrow{OA}-\overrightarrow{OG}]+\beta [\overrightarrow{OB}-\overrightarrow{OG}]=\overrightarrow{0}$ $\iff$ «$(\alpha +\beta )\overrightarrow{OG}=\alpha \overrightarrow{OA}+\beta \overrightarrow{OB}$» soit,
Modèle:AlModèle:Transparentdans le cas d'un barycentre restant à distance finie c.-à-d. «$\alpha +\beta \ne 0$», «$\overrightarrow{OG}=\frac{\alpha }{\alpha +\beta }\overrightarrow{OA}+\frac{\beta }{\alpha +\beta }\overrightarrow{OB}$».

Méthode de construction du barycentre du système de deux points pondérés

Exposé de la méthode de construction du barycentre du système $\{A(1),B(2)\}$ par utilisation du théorème de Modèle:Nobr

Modèle:AlLe point $O$ étant un point quelconque peut être choisi en un des points par exemple $A$ $\Rightarrow$
Modèle:Alla formule précisant le vecteur position du barycentre se réécrit selon $\overrightarrow{AG}=\cancel{\frac{\alpha }{\alpha +\beta }\overrightarrow{AA}}+\frac{\beta }{\alpha +\beta }\overrightarrow{AB}$
Modèle:AlModèle:Transparentétablissant que le point $G$ se trouve sur la droite $(AB)$ plus précisément

• si $\alpha$ et $\beta$ sont tous deux $>0$, $G$ se trouve sur le segment $\left[AB\right]$
  Modèle:Transparentsitué, à partir de $A$ à la fraction $\frac{\beta }{\alpha +\beta }$ de la longueur du segment $\left[AB\right]$,
  Modèle:Transparentles points $A$, $B$ et $G$ sont alignés dans l'ordre $A,G,B$ ;
• si $\beta$ est $>0$ et $\alpha <0$ de valeur absolue $|\alpha |<\beta$, $G$ se trouve au-delà du segment $\left[AB\right]$
  Modèle:Transparentsitué, à partir de $A$ à la fraction $\frac{\beta }{\alpha +\beta }>1$ de la longueur du segment $\left[AB\right]$,
  Modèle:Transparentles points $A$, $B$ et $G$ sont alignés dans l'ordre $A,B,G$ ;
• si $\beta$ est $>0$ et $\alpha <0$ de valeur absolue $|\alpha |>\beta$, $G$ se trouve en-deçà du segment $\left[AB\right]$
  Modèle:Transparentsitué, à partir de $A$ à la fraction $\frac{\beta }{\alpha +\beta }<0$ de la longueur du segment $\left[AB\right]$,
  Modèle:Transparentles points $A$, $B$ et $G$ sont alignés dans l'ordre $G,A,B$.

Modèle:AlExemple de construction : Soit à construire le barycentre du système $\{A(1),B(2)\}$
Modèle:AlModèle:Transparentd'après ce qui précède on en déduit $\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AB}$ c.-à-d. que
Modèle:AlModèle:Transparent$G$ se trouve sur le segment $\left[AB\right]$ au $\frac{2}{3}$ de la longueur du segment à partir de $A$
Modèle:AlModèle:Transparentvoir construction ci-dessus utilisant le théorème de Thalès .

Propriété d'homogénéité

Modèle:AlSi $G$ est le barycentre du système $\{A(\alpha ),B(\beta )\}$ avec $\alpha +\beta \ne 0$, $\Rightarrow$ « pour tout réel $k\ne 0$, le barycentre du système $\{A(k\alpha ),B(k\beta )\}$ est encore $G$».

Modèle:AlDémonstration : la définition du barycentre du système $\{A(\alpha ),B(\beta )\}$ étant $\alpha \overrightarrow{GA}+\beta \overrightarrow{GB}=\overrightarrow{0}$, multipliant cette dernière par $k\ne 0$ et
Modèle:AlModèle:Transparentutilisant la distributivité de la multiplication par un scalaire relativement à l'addition vectorielle $\Rightarrow$
Modèle:AlModèle:Transparent$k\alpha \overrightarrow{GA}+k\beta \overrightarrow{GB}=\overrightarrow{0}$ c.-à-d. la définition du barycentre du système $\{A(k\alpha ),B(k\beta )\}$.

Cas particulier : isobarycentre d'un système de deux points

Modèle:AlOn parle d'« isobarycentre d'un système de deux points » quand les cœfficients qui leur sont affectés sont égaux ou si tous les cœfficients sont égaux à $1$ ;

Modèle:Alpropriété : l'isobarycentre d'un système de deux points est le milieu du segment joignant les deux points.

Barycentre de trois points

Modèle:AlOn généralise aisément la notion de barycentre à un système de trois points pondérés $\dots$

Définition du barycentre d'un système de trois points pondérés

Modèle:AlSoit le système de trois points pondérés $\{A(\alpha ),B(\beta ),C(\gamma )\}$, les cœfficients affectés aux points étant tous trois $\ne 0$, on appelle
Modèle:AlModèle:Transparentbarycentre de ce système de trois points pondérés le point $G$ tel que «$\alpha \overrightarrow{GA}+\beta \overrightarrow{GB}+\gamma \overrightarrow{GC}=\overrightarrow{0}$».

Modèle:AlCondition d'existence et d'unicité : Supposons l'existence du barycentre du système $\{A(\alpha ),B(\beta ),C(\gamma )\}$ et
Modèle:AlModèle:Transparentappliquons les relations de Chasles $\left\{\begin{array}{c}\overrightarrow{GB}=\overrightarrow{GA}+\overrightarrow{AB}\\ \overrightarrow{GC}=\overrightarrow{GA}+\overrightarrow{AC}\end{array}\right\}$ que l'on reporte dans la définition de $G$ soit
Modèle:AlModèle:Transparent$\alpha \overrightarrow{GA}+\beta (\overrightarrow{GA}+\overrightarrow{AB})+\gamma (\overrightarrow{GA}+\overrightarrow{AC})=\overrightarrow{0}$ d'où l'équation suivante $(\alpha +\beta +\gamma )\overrightarrow{GA}=-\beta \overrightarrow{AB}-\gamma \overrightarrow{AC}$ ;
Modèle:AlModèle:Transparenton en déduit une C.N. d'existence du barycentre du système $\{A(\alpha ),B(\beta ),C(\gamma )\}$ qui est «$\alpha +\beta +\gamma \ne 0$» et
Modèle:AlModèle:Transparentsous cette condition on obtient une solution unique «$\overrightarrow{GA}=-\frac{\beta }{\alpha +\beta +\gamma }\overrightarrow{AB}-\frac{\gamma }{\alpha +\beta +\gamma }\overrightarrow{AC}$».
Modèle:AlModèle:TransparentConclusion : le barycentre du système $\{A(\alpha ),B(\beta ),C(\gamma )\}$ n'existe et est unique que si «$\alpha +\beta +\gamma \ne 0$».

Modèle:AlRemarque : On peut prolonger la définition du barycentre du système $\{A(\alpha ),B(\beta ),C(\gamma )\}$ au cas où $\alpha +\beta +\gamma =0$ si on admet que le barycentre puisse être le point à l'infini d'une direction, ainsi
Modèle:AlModèle:Transparentde $(\alpha +\beta +\gamma )\overrightarrow{AG}=\beta \overrightarrow{AB}+\gamma \overrightarrow{AC}$ on déduit que « le barycentre du système des trois points $\{A(\alpha ),B(\beta ),C(\gamma )\}$ avec $\alpha +\beta +\gamma =0$
Modèle:AlModèle:Transparentest le point à l'infini de la direction de $\beta \overrightarrow{AB}+\gamma \overrightarrow{AC}$» .

Vecteur position du barycentre du système de trois points pondérés

Modèle:Al$O$ étant un point quelconque de l'espace, on utilise les relations de Chasles pour $\left\{\begin{array}{c}\overrightarrow{GA}=\overrightarrow{OA}-\overrightarrow{OG}\\ \overrightarrow{GB}=\overrightarrow{OB}-\overrightarrow{OG}\\ \overrightarrow{GC}=\overrightarrow{OC}-\overrightarrow{OG}\end{array}\right\}$ que l'on reporte dans la définition du barycentre «$\alpha \overrightarrow{GA}+\beta \overrightarrow{GB}+\gamma \overrightarrow{GC}=\overrightarrow{0}$» $\Rightarrow$
Modèle:AlModèle:Transparent$\alpha [\overrightarrow{OA}-\overrightarrow{OG}]+\beta [\overrightarrow{OB}-\overrightarrow{OG}]+\gamma [\overrightarrow{OC}-\overrightarrow{OG}]=\overrightarrow{0}\iff (\alpha +\beta +\gamma )\overrightarrow{OG}=\alpha \overrightarrow{OA}+\beta \overrightarrow{OB}+\gamma \overrightarrow{OC}$ soit,
Modèle:AlModèle:Transparentdans le cas d'un barycentre restant à distance finie c.-à-d. «$\alpha +\beta +\gamma \ne 0$», «$\overrightarrow{OG}=\frac{\alpha }{\alpha +\beta +\gamma }\overrightarrow{OA}+\frac{\beta }{\alpha +\beta +\gamma }\overrightarrow{OB}+\frac{\gamma }{\alpha +\beta +\gamma }\overrightarrow{OC}$».

Propriétés de commutativité et d'associativité de la prise de barycentre, notion de barycentre partiel

Modèle:AlLa définition du barycentre d'un système de deux $($ou trois$)$ points pondérés ne précisant pas l'ordre des points, la prise de barycentre est évidemment commutative ;

Modèle:Alla prise de barycentre du système des trois points pondérés $\{A(\alpha ),B(\beta ),C(\gamma )\}$ avec $\alpha +\beta +\gamma \ne 0$
Modèle:AlModèle:Transparentest associative si $\left\{\begin{array}{c}\alpha +\beta \ne 0\\ \beta +\gamma \ne 0\\ \gamma +\alpha \ne 0\end{array}\right\}$, cela se traduisant alors, avec $O$ point quelconque pris pour origine, selon
Modèle:AlModèle:Transparentle vecteur position $\overrightarrow{OG}$ du barycentre du système des trois points pondérés $\{A(\alpha ),B(\beta ),C(\gamma )\}$
Modèle:AlModèle:Transparentpeut se réécrire en réduisant l'une quelconque des sommes vectorielles selon
Modèle:AlModèle:Transparent$\left\{\begin{array}{c}\alpha \overrightarrow{OA}+\beta \overrightarrow{OB}=(\alpha +\beta )\overrightarrow{O{G}_{A,B}}\\ \beta \overrightarrow{OB}+\gamma \overrightarrow{OC}=(\beta +\gamma )\overrightarrow{O{G}_{B,C}}\\ \gamma \overrightarrow{OC}+\alpha \overrightarrow{OA}=(\gamma +\alpha )\overrightarrow{O{G}_{C,A}}\end{array}\right\}$ où les éléments du triplet
Modèle:AlModèle:Transparent$\{G_{A,B},G_{B,C},G_{C,A}\}$ sont respectivement les « barycentres partiels » du système des deux points
Modèle:AlModèle:Transparentpondérés $\{A(\alpha ),B(\beta )\}$, $\{B(\beta ),C(\gamma )\}$ et $\{C(\gamma ),A(\alpha )\}$ ; ainsi
Modèle:AlModèle:Transparentla somme vectorielle $\alpha \overrightarrow{OA}+\beta \overrightarrow{OB}+\gamma \overrightarrow{OC}$ peut se réécrire selon
Modèle:AlModèle:Transparent$\alpha \overrightarrow{OA}+\beta \overrightarrow{OB}+\gamma \overrightarrow{OC}=\left\{\begin{array}{c}(\alpha +\beta )\overrightarrow{O{G}_{A,B}}+\gamma \overrightarrow{OC}\\ (\beta +\gamma )\overrightarrow{O{G}_{B,C}}+\alpha \overrightarrow{OA}\\ (\gamma +\alpha )\overrightarrow{O{G}_{C,A}}+\beta \overrightarrow{OB}\end{array}\right\}$ d'où
Modèle:AlModèle:Transparenttrois façons de réécrire le vecteur position $\overrightarrow{OG}$ du barycentre du système des trois points pondérés $\{A(\alpha ),B(\beta ),C(\gamma )\}$
Modèle:AlModèle:Transparenten utilisant l'un des trois barycentres partiels $\{G_{A,B},G_{B,C},G_{C,A}\}$
Modèle:AlModèle:Transparent«$\overrightarrow{OG}=\left\{\begin{array}{c}\frac{\alpha +\beta }{\alpha +\beta +\gamma }\overrightarrow{O{G}_{A,B}}+\frac{\gamma }{\alpha +\beta +\gamma }\overrightarrow{OC}\\ \frac{\beta +\gamma }{\alpha +\beta +\gamma }\overrightarrow{O{G}_{B,C}}+\frac{\alpha }{\alpha +\beta +\gamma }\overrightarrow{OA}\\ \frac{\gamma +\alpha }{\alpha +\beta +\gamma }\overrightarrow{O{G}_{C,A}}+\frac{\beta }{\alpha +\beta +\gamma }\overrightarrow{OB}\end{array}\right\}$».

Méthode de construction du barycentre du système de trois points pondérés

Modèle:AlLa méthode la plus simple consiste à définir le barycentre partiel entre deux points judicieusement choisis par exemple entre $A(\alpha )$ et $B(\beta )$, le barycentre partiel étant $G_{A,B}(\alpha +\beta )$ puis
Modèle:AlModèle:Transparentà déterminer le barycentre $G(\alpha +\beta +\gamma )$ du système des deux points pondérés $\{G_{A,B}(\alpha +\beta ),C(\gamma )\}$ lequel
Modèle:AlModèle:Transparents'identifie au barycentre du système des trois points pondérés $\{A(\alpha ),B(\beta ),C(\gamma )\}$ :

Disposition des trois atomes d'une molécule d'eau dans le but de déterminer leur barycentre, chaque atome étant affecté de son nombre de masse

Modèle:AlExemple de construction du barycentre du système des trois atomes d'une molécule d'eau, chaque atome étant affecté de son nombre de masse  :
Modèle:AlModèle:Transparentune molécule d'eau est constitué de deux atomes d'hydrogène, notés $H_a$ et $H_b$ pour les distinguer
Modèle:AlModèle:Transparentliés à un atome d'oxygène, noté $O$,
Modèle:AlModèle:Transparentl'angle entre les liaisons étant $\widehat{H_{a}O{H}_b}=\alpha \simeq 105\text{°}$ et
Modèle:AlModèle:Transparentla longueur de chaque liaison $H-O$ étant la même égale à $d\simeq 0,96\text{Å}$,
Modèle:AlModèle:Transparentle nombre de masse d'un atome d'hydrogène étant $1$ et celui d'un atome d'oxygène $16$ ;
Modèle:AlModèle:Transparenton cherche donc le barycentre $G$ du système des trois atomes pondérés $\{O(16),H_a(1),H_b(1)\}$ et pour cela
Modèle:AlModèle:Transparenton détermine d'abord l'isobarycentre $I$ des deux atomes d'hydrogène $H_a$ et $H_b$ qui est
Modèle:AlModèle:Transparentau milieu du segment joignant ces derniers , il est donc
Modèle:AlModèle:Transparentsur la bissectrice de l'angle $\widehat{H_{a}O{H}_b}=\alpha$ situé
Modèle:AlModèle:Transparentà la distance $OI=OH\cos \left(\frac{\alpha }{2}\right)$ de l’atome d'oxygène, soit numériquement,
Modèle:AlModèle:Transparent$OI\simeq 0,96\times \cos (52,5\text{°})$ en $\text{Å}$ ou $OI\simeq 0,584\text{Ǻ}$, puis
Modèle:AlModèle:Transparenton détermine le barycentre $G$ des deux points pondérés $\{O(16),I(2)\}$, $G$ étant sur la bissectrice de l'angle $\widehat{H_{a}O{H}_b}=\alpha$
Modèle:AlModèle:Transparenttel que $\overrightarrow{OG}=\cancel{\frac{16}{18}\overrightarrow{OO}}+\frac{2}{18}\overrightarrow{OI}=\frac{1}{9}\overrightarrow{OI}$,
Modèle:AlModèle:Transparentà la distance $OG=\frac{OI}{9}\simeq \frac{0,584}{9}$ en $\text{Å}$ soit $OG\simeq 0,065\text{Ǻ}$.

Isobarycentre d'un système de trois points non alignés, conséquence sur la propriété des médianes d'un triangle quelconque

Modèle:AlOn parle d'« isobarycentre d'un système de trois points » quand les cœfficients qui leur sont affectés sont égaux ou si tous les cœfficients sont égaux à $1$.

Schéma d'un triangle $ABC$ quelconque avec tracé des trois médianes $A{A}^{\prime }$ issue de $A$, $B{B}^{\prime }$ issue de $B$ et $C{C}^{\prime }$ issue de $C$, propriété de concours de ces trois médianes en $G$ appelé centre de gravité du triangle

Modèle:AlPropriété : l'isobarycentre du système de trois points $\{A(1),B(1),C(1)\}$ peut se déterminer en faisant intervenir l'un des trois isobarycentres partiels
Modèle:AlModèle:Transparent$[$dans ce qui suit les trois points sont non alignés de façon à former un triangle$]$ :
Modèle:AlModèle:Transparent$\bullet$utiliser l'isobarycentre partiel du système $\{B(1),C(1)\}$ qui est $A^{\prime }$ milieu du segment $\left[BC\right]$ puis
Modèle:AlModèle:Transparenten déduire $G$ comme barycentre du système des deux points $\{A(1),A^{\prime }(2)\}$ donc
Modèle:AlModèle:Transparenttel que $\overrightarrow{AG}=\cancel{\frac{1}{3}\overrightarrow{AA}}+\frac{2}{3}\overrightarrow{A{A}^{\prime }}$ établissant que
Modèle:AlModèle:Transparent$G$ se trouve sur la médiane $\left(A{A}^{\prime }\right)$ au $\frac{2}{3}$ de la longueur de la médiane à partir de $A$ ou
Modèle:AlModèle:Transparent$\bullet$utiliser l'isobarycentre partiel du système $\{A(1),C(1)\}$ qui est $B^{\prime }$ milieu du segment $\left[AC\right]$ puis
Modèle:AlModèle:Transparenten déduire $G$ comme barycentre du système des deux points $\{B(1),B^{\prime }(2)\}$ donc
Modèle:AlModèle:Transparenttel que $\overrightarrow{BG}=\cancel{\frac{1}{3}\overrightarrow{BB}}+\frac{2}{3}\overrightarrow{B{B}^{\prime }}$ établissant que
Modèle:AlModèle:Transparent$G$ se trouve sur la médiane $\left(B{B}^{\prime }\right)$ au $\frac{2}{3}$ de la longueur de la médiane à partir de $B$ ou enfin
Modèle:AlModèle:Transparent$\bullet$utiliser l'isobarycentre partiel du système $\{A(1),B(1)\}$ qui est $C^{\prime }$ milieu du segment $\left[AB\right]$ puis
Modèle:AlModèle:Transparenten déduire $G$ comme barycentre du système des deux points $\{C(1),C^{\prime }(2)\}$ donc
Modèle:AlModèle:Transparenttel que $\overrightarrow{CG}=\cancel{\frac{1}{3}\overrightarrow{CC}}+\frac{2}{3}\overrightarrow{C{C}^{\prime }}$ établissant que
Modèle:AlModèle:Transparent$G$ se trouve sur la médiane $\left(C{C}^{\prime }\right)$ au $\frac{2}{3}$ de la longueur de la médiane à partir de $C$ ;

Modèle:AlModèle:Transparenton en déduit que les trois médianes d'un triangle quelconque sont concourantes, le point de concours $G$, appelé « centre de gravité du triangle »,
Modèle:AlModèle:Transparentétant, sur chaque médiane, au $\frac{2}{3}$ de sa longueur à partir du sommet ;

Modèle:AlModèle:Transparentle centre de gravité $G$ du triangle $ABC$ est donc défini par «$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$»,
Modèle:AlModèle:Transparentson vecteur position relativement à un point $O$ quelconque étant «$\overrightarrow{OG}=\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}$» .

Barycentre de n points

Modèle:AlOn généralise la notion de barycentre à un système de n points pondérés, $n\in {\mathbb{N}}^{*}/\left\{1\right\}$ $\dots$

Définition du barycentre d'un système de n points pondérés

Modèle:AlSoit le système de $n$ points pondérés $\{A_1({\alpha }_1),A_2({\alpha }_2),\dots ,A_k({\alpha }_k),\dots ,A_n({\alpha }_n)\}$, les cœfficients affectés aux points étant tous $\ne 0$, on appelle
Modèle:AlModèle:Transparentbarycentre de ce système de n points pondérés le point $G$ tel que «$\sum _{k=1}^n{\alpha }_k\overrightarrow{G{A}_k}=\overrightarrow{0}$».

Modèle:AlCondition d'existence et d'unicité : On admet qu'une C.N. d'existence du barycentre du système $\{A_1({\alpha }_1),A_2({\alpha }_2),\dots ,A_k({\alpha }_k),\dots ,A_n({\alpha }_n)\}$ est «$\sum _{k=1}^n{\alpha }_k\ne 0$» et
Modèle:AlModèle:Transparentque sous cette condition on obtient une solution unique.

Notion d'espace affine de direction l'espace vectoriel associé

Modèle:AlÉtant donné un espace vectoriel ${ℰ}_{\text{vect}}$ sur le corps des réels $ℝ$ on appelle
Modèle:AlModèle:Transparentespace affine ${ℰ}_{\text{aff}}$ de direction ${ℰ}_{\text{vect}}$ l'ensemble non vide muni d'une application $\phi$ qui, à chaque bipoint $(A,B)$ de ${ℰ}_{\text{aff}}^2$ associe un élément de ${ℰ}_{\text{vect}}$ noté $\overrightarrow{AB}$
Modèle:AlModèle:Transparentvérifiant les deux propriétés suivantes :
Modèle:AlModèle:Transparent$\bullet$«$\mathrm{\forall }(A,B,C)\in {ℰ}_{\text{aff}}^3$, la relation de Chasles $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$
Modèle:AlModèle:Transparents'applique dans ${ℰ}_{\text{vect}}$» et
Modèle:AlModèle:Transparent$\bullet$«$\mathrm{\forall }A\in {ℰ}_{\text{aff}}$, $\mathrm{\forall }\overrightarrow{v}\in {ℰ}_{\text{vect}}$, il existe un translaté unique de $A$ par $\overrightarrow{v}$» c.-à-d.
Modèle:AlModèle:Transparent«$\mathrm{\exists }!B\in {ℰ}_{\text{aff}}$ tel que $\overrightarrow{AB}=\overrightarrow{v}$» .

Modèle:AlOn définit la dimension de l'espace affine ${ℰ}_{\text{aff}}$ par celle de l'espace vectoriel ${ℰ}_{\text{vect}}$ qui lui est associé ;

Modèle:Alexemples : espace affine de dimension $1$ encore appelé « droite affine » dont la direction est l'espace vectoriel généré par un vecteur $\overrightarrow{i}$ ;

Modèle:AlModèle:Transparentespace affine de dimension $2$ encore appelé « plan affine » dont la direction est l'espace vectoriel généré par $(\overrightarrow{i},\overrightarrow{j})$ deux vecteurs non colinéaires ;

Modèle:AlModèle:Transparentespace affine de dimension $3$ dont la direction est l'espace vectoriel généré par $(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})$ trois vecteurs non coplanaires ;

Modèle:AlModèle:Transparentespace affine de dimension $n⩾4$ dont la direction est l'espace vectoriel généré par ${\left({\overrightarrow{u}}_i\right)}_{i=1\dots n⩾4}$, $n⩾4$ formant une famille libre ,
Modèle:AlModèle:Transparent$[$non concevable par notre cerveau dont l'imaginaire ne peut représenter que trois dimensions au maximum $]$.

Modèle:AlPropriété : si on fixe un point origine $O$ dans l'espace affine ${ℰ}_{\text{aff}}$, il existe une application ${\phi }_O$ de ${ℰ}_{\text{aff}}$ dans sa direction ${ℰ}_{\text{vect}}$
Modèle:AlModèle:Transparentqui, à tout point $M$ de ${ℰ}_{\text{aff}}$ associe le vecteur $\overrightarrow{OM}$ ; cette application ${\phi }_O$ est alors bijective .

Isobarycentre d'un système de quatre points non coplanaires, conséquence sur la propriété des médianes d'un tétraèdre quelconque

Modèle:AlOn parle d'« isobarycentre d'un système de quatre points » quand les cœfficients qui leur sont affectés sont égaux ou si tous les cœfficients sont égaux à $1$.

Schéma d'un tétraèdre $ABCD$ quelconque avec tracé de trois des quatre médianes $A{A}^{\prime }$ issue de $A$, $B{B}^{\prime }$ issue de $B$, $C{C}^{\prime }$ issue de $C$ $(D{D}^{\prime }$ issue de $D$ n'ayant pas été tracée pour ne pas surcharger$)$, propriété de concours de ces quatre médianes en $G$ appelé centre de gravité du tétraèdre

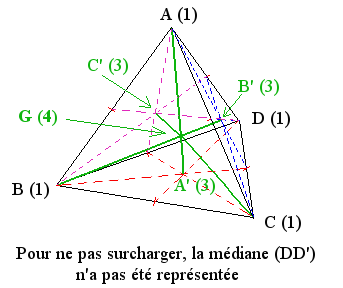
Modèle:AlPropriété : l'isobarycentre du système de quatre points $\{A(1),B(1),C(1),D(1)\}$
Modèle:AlModèle:Transparentpeut se déterminer en faisant intervenir l'un des quatre isobarycentres partiels
Modèle:AlModèle:Transparent$[$dans ce qui suit les quatre points sont non coplanaires de façon à former un tétraèdre$]$ :
Modèle:AlModèle:Transparent$\bullet$utiliser l'isobarycentre partiel $A^{\prime }$ du système $\{B(1),C(1),D(1)\}$,
Modèle:AlModèle:Transparent$A^{\prime }$ étant le centre de gravité de la face $\left(BCD\right)$ puis
Modèle:AlModèle:Transparenten déduire $G$ comme barycentre du système $\{A(1),A^{\prime }(3)\}$ donc
Modèle:AlModèle:Transparenttel que $\overrightarrow{AG}=\cancel{\frac{1}{4}\overrightarrow{AA}}+\frac{3}{4}\overrightarrow{A{A}^{\prime }}$ établissant que
Modèle:AlModèle:Transparent$G$ se trouve sur la médiane $\left(A{A}^{\prime }\right)$
Modèle:AlModèle:Transparentau $\frac{3}{4}$ de la longueur de la médiane à partir de $A$ ou
Modèle:AlModèle:Transparent$\bullet$utiliser l'isobarycentre partiel $B^{\prime }$ du système $\{A(1),C(1),D(1)\}$,
Modèle:AlModèle:Transparent$B^{\prime }$ étant le centre de gravité de la face $\left(ACD\right)$ puis
Modèle:AlModèle:Transparenten déduire $G$ comme barycentre du système $\{B(1),B^{\prime }(3)\}$ donc
Modèle:AlModèle:Transparenttel que $\overrightarrow{BG}=\cancel{\frac{1}{4}\overrightarrow{BB}}+\frac{3}{4}\overrightarrow{B{B}^{\prime }}$ établissant que
Modèle:AlModèle:Transparent$G$ se trouve sur la médiane $\left(B{B}^{\prime }\right)$
Modèle:AlModèle:Transparentau $\frac{3}{4}$ de la longueur de la médiane à partir de $B$ ou
Modèle:AlModèle:Transparent$\bullet$utiliser l'isobarycentre partiel $C^{\prime }$ du système $\{A(1),B(1),D(1)\}$,
Modèle:AlModèle:Transparent$C^{\prime }$ étant le centre de gravité de la face $\left(ABD\right)$ puis
Modèle:AlModèle:Transparenten déduire $G$ comme barycentre du système $\{C(1),C^{\prime }(3)\}$ donc tel que $\overrightarrow{CG}=\cancel{\frac{1}{4}\overrightarrow{CC}}+\frac{3}{4}\overrightarrow{C{C}^{\prime }}$ établissant que
Modèle:AlModèle:Transparent$G$ se trouve sur la médiane $\left(C{C}^{\prime }\right)$ au $\frac{3}{4}$ de la longueur de la médiane à partir de $C$ ou enfin
Modèle:AlModèle:Transparent$\bullet$utiliser l'isobarycentre partiel $D^{\prime }$ du système $\{A(1),B(1),C(1)\}$, $D^{\prime }$ étant le centre de gravité de la face $\left(ABC\right)$ puis
Modèle:AlModèle:Transparenten déduire $G$ comme barycentre du système $\{D(1),D^{\prime }(3)\}$ donc tel que $\overrightarrow{DG}=\cancel{\frac{1}{4}\overrightarrow{DD}}+\frac{3}{4}\overrightarrow{D{D}^{\prime }}$ établissant que
Modèle:AlModèle:Transparent$G$ se trouve sur la médiane $\left(D{D}^{\prime }\right)$ au $\frac{3}{4}$ de la longueur de la médiane à partir de $D$ ;

Modèle:AlModèle:Transparenton en déduit que les quatre médianes d'un tétraèdre quelconque sont concourantes, le point de concours $G$, appelé « centre de gravité du tétraèdre »,
Modèle:AlModèle:Transparentétant, sur chaque médiane, au $\frac{3}{4}$ de sa longueur à partir du sommet ;

Modèle:AlModèle:Transparentle centre de gravité $G$ du tétraèdre $ABCD$ est donc défini selon la relation «$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$»,
Modèle:AlModèle:Transparentson vecteur position relativement à un point $O$ quelconque étant «$\overrightarrow{OG}=\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}}{4}$» .

Notion de fonction vectorielle de Leibniz

Modèle:AlOn se place dans un espace affine ${ℰ}_{\text{aff}}$ de direction l'espace vectoriel ${ℰ}_{\text{vect}}$ tous deux de dimension $p\in {\mathbb{N}}^{*}$ ;

${\left(A_k\right)}_{k=1,\dots ,n⩾p+1}$

une famille de

$n$

points de

${ℰ}_{\text{aff}}$

et

${\left({\alpha }_k\right)}_{k=1,\dots ,n⩾p+1}$

une famille de

$n$

scalaires réels, on appelle

fonction vectorielle de Leibniz associée au système de $n$ points pondérés ${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$ de l'espace affine ${ℰ}_{\text{aff}}$,
« l'application $\overrightarrow{f}$ de ${ℰ}_{\text{aff}}$ dans ${ℰ}_{\text{vect}}$ qui, au point $M\in {ℰ}_{\text{aff}}$ associe le vecteur $\overrightarrow{f}(M)=\sum _{k=1}^n{\alpha }_k\overrightarrow{M{A}_k}\in {ℰ}_{\text{vect}}$».

Modèle:AlPropriétés : si

$\sum _{k=1}^{n⩾p+1}{\alpha }_k\ne 0$

, la fonction vectorielle de Leibniz associée au système de

$n$

points pondérés

${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$

de l'espace affine

${ℰ}_{\text{aff}}$

Modèle:AlModèle:Transparents'annule pour un unique point

$G\in {ℰ}_{\text{aff}}$

définissant le barycentre du système des

$n$

points pondérés

${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$

 ;

en conclusion « si $\sum _{k=1}^{n⩾p+1}{\alpha }_k\ne 0$», «$\mathrm{\exists }!G\in {ℰ}_{\text{aff}}$ tel que $\overrightarrow{f}(G)=\sum _{k=1}^{n⩾p+1}{\alpha }_k\overrightarrow{G{A}_k}=\overrightarrow{0}$» ;

Modèle:AlModèle:Transparent« si $\sum _{k=1}^{n⩾p+1}{\alpha }_k\ne 0$», la fonction vectorielle de Leibniz associée au système de $n$ points pondérés ${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$ de l'espace affine ${ℰ}_{\text{aff}}$
Modèle:AlModèle:Transparentpeut être simplifiée en utilisant le barycentre $G$ du système des $n$ points pondérés ${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$
Modèle:AlModèle:Transparentselon «$\overrightarrow{f}(M)=\sum _{k=1}^{n⩾p+1}{\alpha }_k\overrightarrow{M{A}_k}=\left(\sum _{k=1}^{n⩾p+1}{\alpha }_k\right)\overrightarrow{MG}$» ;

Modèle:AlModèle:Transparent« si

$\sum _{k=1}^{n⩾p+1}{\alpha }_k\ne 0$

», avec

$O\in {ℰ}_{\text{aff}}$

choisi comme origine du vecteur position du barycentre

$G$

du système des

$n$

points pondérés

${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$

, on obtient

«$\overrightarrow{OG}=\frac{\overrightarrow{f}(O)}{\sum _{k=1}^{n⩾p+1}{\alpha }_k}=\frac{\sum _{k=1}^{n⩾p+1}{\alpha }_k\overrightarrow{O{A}_k}}{\sum _{k=1}^{n⩾p+1}{\alpha }_k}$».

Modèle:AlRemarque : « si $\sum _{k=1}^{n⩾p+1}{\alpha }_k=0$», on démontre que la fonction vectorielle de Leibniz associée au système de $n$ points pondérés de l'espace affine ${ℰ}_{\text{aff}}$ à savoir ${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$
Modèle:AlModèle:Transparentest constante ;
Modèle:AlModèle:Transparent« avec ${\alpha }_1\ne 0$» la constante s'écrit «$\overrightarrow{f}(M)=\sum _{k=1}^{n⩾p+1}{\alpha }_k\overrightarrow{M{A}_k}={\alpha }_1\overrightarrow{G_1{A}_1}$ avec $G_1$ le barycentre du système des $n-1$ points pondérés autres que $A_1$»,
Modèle:Transparenten effet si ${\alpha }_1\ne 0$, « la somme $\sum _{k=1}^{n⩾p+1}{\alpha }_k=0$ se réécrit $\sum _{k=2}^{n⩾p+1}{\alpha }_k=-{\alpha }_1\ne 0$» $\Rightarrow$ « l'existence et l'unicité du barycentre $G_1$ des $n-1$ points pondérés
Modèle:Transparent${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=2,\dots ,n⩾p+1}$» soit
Modèle:Transparent«$\sum _{k=2}^{n⩾p+1}{\alpha }_k\overrightarrow{M{A}_k}=\left(\sum _{k=2}^{n⩾p+1}{\alpha }_k\right)\overrightarrow{M{G}_1}$» ou encore
Modèle:Transparent«$\sum _{k=2}^{n⩾p+1}{\alpha }_k\overrightarrow{M{A}_k}=-{\alpha }_1\overrightarrow{M{G}_1}$» que l'on reporte dans la définition de
Modèle:Transparentla fonction vectorielle de Leibniz
Modèle:AlModèle:Transparent«$\overrightarrow{f}(M)={\alpha }_1\overrightarrow{M{A}_1}+\sum _{k=2}^{n⩾p+1}{\alpha }_k\overrightarrow{M{A}_k}={\alpha }_1\overrightarrow{M{A}_1}-{\alpha }_1\overrightarrow{M{G}_1}$» soit, par utilisation de la relation de Chasles
Modèle:AlModèle:Transparent«$\overrightarrow{f}(M)={\alpha }_1[\overrightarrow{M{A}_1}-\overrightarrow{M{G}_1}]={\alpha }_1\overrightarrow{G_1{A}_1}$» C.Q.F.D. .

Utilisation de la notion de barycentre à la détermination de lieu de points défini par une relation scalaire particulière

Lieu des points M tel que le rapport des distances à deux points distincts d'un espace affine euclidien à trois dimensions soit égal à un réel positif différent de un

Modèle:AlEspace vectoriel euclidien : un espace vectoriel est dit « euclidien » si on définit sur lui un produit scalaire de deux vecteurs .

Modèle:AlEspace affine euclidien : un espace affine est dit « euclidien » si l'espace vectoriel direction de l'espace affine est « euclidien »,
Modèle:AlModèle:Transparentla conséquence étant la possibilité de mesurer distances et angles dans l'espace affine « euclidien » ;

Modèle:AlModèle:Transparentla distance entre deux points de l'espace affine « euclidien »

${ℰ}_{\text{aff}}$

de direction l'espace vectoriel

${ℰ}_{\text{vect}}$

est l'application

$d$

de

${ℰ}_{\text{aff}}\times {ℰ}_{\text{aff}}$

dans

${ℝ}_{+}$

défini par

«$(A,B)\stackrel{d}{\mapsto }\Vert \overrightarrow{AB}\Vert =\sqrt{\overrightarrow{AB}\cdot \overrightarrow{AB}}=\sqrt{\stackrel{2}{\overrightarrow{AB}}}$» ;

Modèle:AlModèle:Transparentl'angle entre deux bipoints de l'espace affine « euclidien »

${ℰ}_{\text{aff}}$

de direction l'espace vectoriel

${ℰ}_{\text{vect}}$

est l'application

$\alpha$

de

${ℰ}_{\text{aff}}^2\times {ℰ}_{\text{aff}}^2$

dans

${ℝ}_{+}$

défini par

«$\{(A,B),(C,D)\}\stackrel{\alpha }{\mapsto }\arccos \left[\frac{\overrightarrow{AB}\cdot \overrightarrow{CD}}{\Vert \overrightarrow{AB}\Vert \Vert \overrightarrow{CD}\Vert }\right]$» .

Modèle:AlProblème posé : Trouver le lieu des points $M$ de l'espace affine « euclidien » de dimension $3$ tel que, $(A,B)$ étant deux points distincts de cet espace,
Modèle:AlModèle:Transparentle rapport des distances séparant $M$ de chacun des points est un réel $>0$, $\ne 1$, ou
Modèle:AlModèle:Transparenttel que «$\frac{d(M,A)}{d(M,B)}=k\in {ℝ}_{+}^{*}\setminus \left\{1\right\}$» .

Modèle:AlSolution : La relation de définition de $M\in {ℰ}_{\text{aff},3}$ étant «$\Vert \overrightarrow{MA}\Vert =k\Vert \overrightarrow{MB}\Vert$ avec $k\in {ℝ}_{+}^{*}\setminus \left\{1\right\}$», $(A,B)\in {ℰ}_{\text{aff},3}^2$ et $A\ne B$,
Modèle:AlModèle:Transparentpeut se réécrire «$\Vert \overrightarrow{MA}{\Vert }^2=k^2\Vert \overrightarrow{MB}{\Vert }^2$» ou encore Modèle:Nobr soit finalement
Modèle:AlModèle:Transparent«$(\overrightarrow{MA}-k\overrightarrow{MB})\cdot (\overrightarrow{MA}+k\overrightarrow{MB})=0$»  ;

Modèle:AlModèle:Transparenton réalise alors la réduction des sommes vectorielles «

$\left\{\begin{array}{c}\overrightarrow{MA}-k\overrightarrow{MB}\\ \overrightarrow{MA}+k\overrightarrow{MB}\end{array}\right\}$

» en utilisant respectivement les barycentres

$\left\{\begin{array}{c}{G}_{-}\\ G_{+}\end{array}\right\}$

du système des deux points pondérés

$\left\{\begin{array}{c}[A(1),B(-k)]\\ [A(1),B(+k)]\end{array}\right\}$

,
Modèle:AlModèle:Transparentchaque barycentre existant et étant unique car
Modèle:AlModèle:Transparentla somme des cœfficients affectant les points de chacun des systèmes est non nulle
Modèle:Transparentsoit «

$\left\{\begin{array}{c}\overrightarrow{MA}-k\overrightarrow{MB}=(1-k)\overrightarrow{M{G}_{-}}\\ \overrightarrow{MA}+k\overrightarrow{MB}=(1+k)\overrightarrow{M{G}_{+}}\end{array}\right\}$

»
Modèle:AlModèle:Transparentce qui permet de réécrire la relation de définition du lieu cherché des points

$M$

selon «

$(1-k^2)\overrightarrow{M{G}_{-}}\cdot \overrightarrow{M{G}_{+}}=0$

» ou,
Modèle:AlModèle:Transparentavec

$k^2\ne 1$

, «

$\overrightarrow{M{G}_{-}}\cdot \overrightarrow{M{G}_{+}}=0$

» soit enfin

« le lieu des points $M$ tel que $\frac{d(M,A)}{d(M,B)}=k\in {ℝ}_{+}^{*}\setminus \left\{1\right\}$ est la sphère de diamètre $\left[G_{-}{G}_{+}\right]$» où
«$G_{-}$ est le barycentre du système $\{A(1),B(-k)\}$» et «$G_{+}$ celui du système $\{A(1),B(+k)\}$».

Notion de fonction scalaire de Leibniz

Modèle:AlOn se place dans un espace affine euclidien ${ℰ}_{\text{aff}}$ de direction l'espace vectoriel euclidien ${ℰ}_{\text{vect}}$ tous deux de dimension $p\in {\mathbb{N}}^{*}$ ;

${\left(A_k\right)}_{k=1,\dots ,n⩾p+1}$

une famille de

$n$

points de

${ℰ}_{\text{aff}}$

et

${\left({\alpha }_k\right)}_{k=1,\dots ,n⩾p+1}$

une famille de

$n$

scalaires réels, on appelle

fonction scalaire de Leibniz associée au système de $n$ points pondérés ${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$ de l'espace affine euclidien ${ℰ}_{\text{aff}}$,
« l'application $f$ de ${ℰ}_{\text{aff}}$ dans $ℝ$ qui, au point $M\in {ℰ}_{\text{aff}}$ associe le scalaire $f(M)=\sum _{k=1}^n{\alpha }_k\stackrel{2}{\overrightarrow{M{A}_k}}\in ℝ$».

Modèle:AlPropriétés : « si $\sum _{k=1}^{n⩾p+1}{\alpha }_k\ne 0$», la fonction scalaire de Leibniz associée au système de $n$ points pondérés ${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$ de l'espace affine euclidien ${ℰ}_{\text{aff}}$
Modèle:AlModèle:Transparentpeut être réduite, en utilisant $G\in {ℰ}_{\text{aff}}$ le barycentre du système des n points pondérés ${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$, selon
Modèle:AlModèle:Transparent«$f(M)=\sum _{k=1}^n{\alpha }_k\stackrel{2}{\overrightarrow{M{A}_k}}=f(G)+\left(\sum _{k=1}^{n⩾p+1}{\alpha }_k\right)\stackrel{2}{\overrightarrow{MG}}$»  ;

Modèle:AlModèle:Transparenten effet, par relation de Chasles , $\overrightarrow{M{A}_k}=\overrightarrow{MG}+\overrightarrow{G{A}_k}$ $\Rightarrow$ ${\alpha }_k\stackrel{2}{\overrightarrow{M{A}_k}}={\alpha }_k\stackrel{2}{\overrightarrow{MG}}+{\alpha }_k\stackrel{2}{\overrightarrow{G{A}_k}}+2\overrightarrow{MG}\cdot {\alpha }_k\overrightarrow{G{A}_k}$ soit,
Modèle:AlModèle:Transparenten reportant dans la relation de définition de la fonction scalaire de Leibniz et
Modèle:AlModèle:Transparenten factorisant dans les produits de scalaires et les produits scalaires de vecteurs
Modèle:AlModèle:Transparent«$f(M)=\left(\sum _{k=1}^{n⩾p+1}{\alpha }_k\right)\stackrel{2}{\overrightarrow{MG}}+\left(\sum _{k=1}^{n⩾p+1}{\alpha }_k\stackrel{2}{\overrightarrow{G{A}_k}}\right)+2\overrightarrow{MG}\cdot \left(\sum _{k=1}^{n⩾p+1}{\alpha }_k\overrightarrow{G{A}_k}\right)$» ou,
Modèle:AlModèle:Transparentpar définition «$\sum _{k=1}^{n⩾p+1}{\alpha }_k\overrightarrow{G{A}_k}=\overrightarrow{0}$ du barycentre $G$ du système des $n$ points pondérés ${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$» ,
Modèle:AlModèle:Transparentla fonction scalaire de Leibniz se réécrit «$f(M)=\left(\sum _{k=1}^{n⩾p+1}{\alpha }_k\right)\stackrel{2}{\overrightarrow{MG}}+\left(\sum _{k=1}^{n⩾p+1}{\alpha }_k\stackrel{2}{\overrightarrow{G{A}_k}}\right)=\left(\sum _{k=1}^{n⩾p+1}{\alpha }_k\right)\stackrel{2}{\overrightarrow{MG}}+f(G)$» ;

Modèle:AlModèle:Transparent« si

$\sum _{k=1}^{n⩾p+1}{\alpha }_k\ne 0$

», avec

$O\in {ℰ}_{\text{aff}}$

choisi comme origine du vecteur position du barycentre

$G$

du système des

$n$

points pondérés

${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$

, on obtient

«$\stackrel{2}{\overrightarrow{OG}}=\frac{f(O)-f(G)}{\sum _{k=1}^{n⩾p+1}{\alpha }_k}=\frac{\sum _{k=1}^{n⩾p+1}{\alpha }_k[\stackrel{2}{\overrightarrow{O{A}_k}}-\stackrel{2}{\overrightarrow{G{A}_k}}]}{\sum _{k=1}^{n⩾p+1}{\alpha }_k}$».

Modèle:AlRemarque : « si $\sum _{k=1}^{n⩾p+1}{\alpha }_k=0$», ayant admis que la fonction vectorielle de Leibniz $\overrightarrow{f}(M)=\sum _{k=1}^{n⩾p+1}{\alpha }_k\overrightarrow{M{A}_k}$ associée au système de $n$ points pondérés de l'espace affine euclidien ${ℰ}_{\text{aff}}$ à savoir
Modèle:AlModèle:Transparentà ${\left\{A_k\left({\alpha }_k\right)\right\}}_{k=1,\dots ,n⩾p+1}$ est constante s'écrivant, « si ${\alpha }_1\ne 0$» ,
Modèle:AlModèle:Transparent«$\overrightarrow{f}(M)={\alpha }_1\overrightarrow{G_1{A}_1}$ avec $G_1$ le barycentre du système des $n-1$ points pondérés autres que $A_1$» soit
Modèle:AlModèle:Transparentla réduction de la fonction scalaire de Leibniz selon «$f(M)=\sum _{k=1}^n{\alpha }_k\stackrel{2}{\overrightarrow{M{A}_k}}=f(O)+2{\alpha }_1\overrightarrow{MO}\cdot \overrightarrow{G_1{A}_1}$» avec $O$ point arbitrairement fixé ;

Modèle:AlModèle:Transparenten effet « si ${\alpha }_1\ne 0$ avec $\sum _{k=1}^{n⩾p+1}{\alpha }_k=0$», $\Rightarrow$ $\sum _{k=2}^{n⩾p+1}{\alpha }_k=-{\alpha }_1\ne 0$ $\Rightarrow$ l'existence et l'unicité du barycentre $G_1$ des $n-1$ points pondérés autres que $A_1$ ;

Modèle:AlModèle:Transparent$O$ étant un point de ${ℰ}_{\text{aff}}$ choisi arbitrairement, l'utilisation de la relation de Chasles conduisant à $\overrightarrow{M{A}_k}=\overrightarrow{MO}+\overrightarrow{O{A}_k}$ donne,
Modèle:AlModèle:Transparenten reportant dans la définition de la fonction scalaire de Leibniz avec ${\alpha }_k\stackrel{2}{\overrightarrow{M{A}_k}}={\alpha }_k\stackrel{2}{\overrightarrow{MO}}+{\alpha }_k\stackrel{2}{\overrightarrow{O{A}_k}}+2\overrightarrow{MO}\cdot \left({\alpha }_k\overrightarrow{O{A}_k}\right)$ $\Rightarrow$
Modèle:AlModèle:Transparent«$f(M)=\sum _{k=1}^{n⩾p+1}{\alpha }_k\stackrel{2}{\overrightarrow{M{A}_k}}=\cancel{\left(\sum _{k=1}^{n⩾p+1}{\alpha }_k\right)\stackrel{2}{\overrightarrow{MO}}+}\left(\sum _{k=1}^{n⩾p+1}{\alpha }_k\stackrel{2}{\overrightarrow{O{A}_k}}\right)+2\overrightarrow{MO}\cdot \left(\sum _{k=1}^{n⩾p+1}{\alpha }_k\overrightarrow{O{A}_k}\right)$» obtenue
Modèle:AlModèle:Transparenten factorisant dans les produits de scalaires et les produits scalaires de vecteurs et en utilisant la nullité de la somme des cœfficients, ou encore,
Modèle:AlModèle:Transparent«$f(M)=f(O)+2\overrightarrow{MO}\cdot \overrightarrow{f}(O)$» où «$\overrightarrow{f}(O)=\sum _{k=1}^{n⩾p+1}{\alpha }_k\overrightarrow{O{A}_k}={\alpha }_1\overrightarrow{G_1{A}_1}$ dans la mesure où ${\alpha }_1\ne 0$» C.Q.F.D. .

Prolongement de la notion de barycentre à un système continu de points pondérés

Modèle:AlOn considère maintenant un système continu de points en chacun desquels est affectée une densité de cœfficient continue par morceaux,
Modèle:AlModèle:Transparentces points décrivant une courbe, une surface ou une expansion tridimensionnelle continues dans un espace affine euclidien à trois dimensions
Modèle:AlModèle:Transparentdans lequel est définie l'intégrabilité.

Barycentre d'un système continu de points décrivant une courbe continue en chacun desquels est affectée une densité linéique de cœfficient continue par morceaux

Modèle:AlSoit une courbe continue $\left(\mathrm{\Gamma }\right)$ de point générique $P$ affecté d'une densité linéique de cœfficient $\lambda (P)$ continue par morceaux, on y définit
Modèle:AlModèle:Transparentle barycentre $G$ de ce système de points $\{P[\lambda (P)],P\in \left(\mathrm{\Gamma }\right)\}$ par «$\underset{P\in \left(\mathrm{\Gamma }\right)}{\int }\lambda (P)\overrightarrow{GP}d{s}_P=\overrightarrow{0}$» où $s_P$ est l'abscisse curviligne du point générique sur $\left(\mathrm{\Gamma }\right)$ ;

Modèle:Alon établit que la condition d'existence et d'unicité du barycentre $G$ du système de points $\{P[\lambda (P)],P\in \left(\mathrm{\Gamma }\right)\}$ est «$\underset{P\in \left(\mathrm{\Gamma }\right)}{\int }\lambda (P)d{s}_P\ne 0$»  ;

Modèle:Alon démontre aussi que le vecteur position du barycentre $G$ du système de points $\{P[\lambda (P)],P\in \left(\mathrm{\Gamma }\right)\}$ avec $O$ point quelconque de l'espace affine euclidien à trois dimensions
Modèle:AlModèle:Transparentdans lequel est définie la courbe $\left(\mathrm{\Gamma }\right)$
Modèle:AlModèle:Transparents'écrit «$\overrightarrow{OG}=\frac{\underset{P\in \left(\mathrm{\Gamma }\right)}{\int }\lambda (P)\overrightarrow{OP}d{s}_P}{\underset{P\in \left(\mathrm{\Gamma }\right)}{\int }\lambda (P)d{s}_P}$» .

Barycentre d'un système continu de points décrivant une surface continue en chacun desquels est affectée une densité surfacique de cœfficient continue par morceaux

Modèle:AlSoit une surface continue $\left(\mathrm{\Sigma }\right)$ de point générique $P$ affecté d'une densité surfacique de cœfficient $\sigma (P)$ continue par morceaux, on y définit
Modèle:AlModèle:Transparentle barycentre $G$ de ce système de points $\{P[\sigma (P)],P\in \left(\mathrm{\Sigma }\right)\}$ par «$\underset{P\in \left(\mathrm{\Sigma }\right)}{\iint }\sigma (P)\overrightarrow{GP}d{S}_P=\overrightarrow{0}$» où $d{S}_P$ est l'aire élémentaire définie au point générique sur $\left(\mathrm{\Sigma }\right)$ ;

Modèle:Alon établit que la condition d'existence et d'unicité du barycentre $G$ du système de points $\{P[\sigma (P)],P\in \left(\mathrm{\Sigma }\right)\}$ est «$\underset{P\in \left(\mathrm{\Sigma }\right)}{\iint }\sigma (P)d{S}_P\ne 0$»  ;

Modèle:Alon démontre aussi que le vecteur position du barycentre $G$ du système de points $\{P[\sigma (P)],P\in \left(\mathrm{\Sigma }\right)\}$ avec $O$ point quelconque de l'espace affine euclidien à trois dimensions
Modèle:AlModèle:Transparentdans lequel est définie la surface $\left(\mathrm{\Sigma }\right)$
Modèle:AlModèle:Transparents'écrit «$\overrightarrow{OG}=\frac{\underset{P\in \left(\mathrm{\Sigma }\right)}{\iint }\sigma (P)\overrightarrow{OP}d{S}_P}{\underset{P\in \left(\mathrm{\Sigma }\right)}{\iint }\sigma (P)d{S}_P}$» .

Barycentre d'un système continu de points décrivant une expansion tridimensionnelle continue en chacun desquels est affectée une densité volumique de cœfficient continue par morceaux

Modèle:AlSoit une expansion tridimensionnelle continue $\left(𝒱\right)$ de point générique $P$ affecté d'une densité volumique de cœfficient $\mu (P)$ continue par morceaux, on y définit
Modèle:AlModèle:Transparentle barycentre $G$ de ce système de points $\{P[\mu (P)],P\in \left(𝒱\right)\}$ par «$\underset{P\in \left(𝒱\right)}{\iiint }\mu (P)\overrightarrow{GP}d{𝒱}_P=\overrightarrow{0}$» où $d{𝒱}_P$ est le volume élémentaire défini au point générique dans $\left(𝒱\right)$ ;

Modèle:Alon établit que la condition d'existence et d'unicité du barycentre $G$ du système de points $\{P[\mu (P)],P\in \left(𝒱\right)\}$ est «$\underset{P\in \left(𝒱\right)}{\iiint }\mu (P)d{𝒱}_P\ne 0$»  ;

Modèle:Alon démontre aussi que le vecteur position du barycentre $G$ du système de points $\{P[\mu (P)],P\in \left(𝒱\right)\}$ avec $O$ point quelconque de l'espace affine euclidien à trois dimensions
Modèle:AlModèle:Transparentdans lequel est définie l'expansion $\left(𝒱\right)$
Modèle:AlModèle:Transparents'écrit «$\overrightarrow{OG}=\frac{\underset{P\in \left(𝒱\right)}{\iiint }\mu (P)\overrightarrow{OP}d{𝒱}_P}{\underset{P\in \left(𝒱\right)}{\iiint }\mu (P)d{𝒱}_P}$» .