Signaux physiques (PCSI)/Oscillateur harmonique
Modèle:AlUn « oscillateur mécanique à un degré de liberté » est un solide assimilable à un point oscillant sur une courbe fixe autour d'une position d'équilibre, la trajectoire étant rectiligne ou curviligne par exemple circulaire ; dans le cas rectiligne, la position de est repérée à la date par son abscisse , c'est ce cas que nous envisagerons dans ce chapitre ;
Modèle:All'oscillateur est « harmonique » si le mouvement de est décrit par une fonction « sinusoïdale » du temps bien sûr, le mouvement n'est sinusoïdal que sur une durée pendant laquelle l'influence des frottements est négligeable, seul cas envisagé dans ce chapitre.
Description
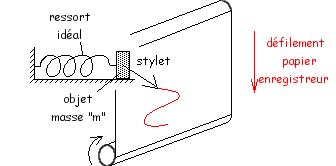
Modèle:AlOn utilise :
- un ressort idéal, c.-à-d. de masse négligeable par rapport aux autres masses à spires non jointives[1], parfaitement élastique pourvu qu'on reste dans son domaine d'élasticité[2], de longueur à vide , de raideur [3],
- un objet de masse accroché à une extrémité du ressort, l'autre extrémité de ce dernier étant fixe, le tout pouvant glisser sans frottement sur un plan horizontal et
- éventuellement un guide rectiligne horizontal, par exemple un banc à coussin d'air non représenté sur le schéma à l'axe du ressort imposant au solide un mouvement rigoureusement rectiligne ;
Modèle:Alde façon à repérer le mouvement de l'objet, on lui a fixé un stylet qui laissera sa position horizontale sur une feuille de papier enregistreur défilant verticalement à vitesse constante ; ainsi nous aurons un axe vertical orienté vers le haut à l'axe des temps et un axe horizontal orienté vers la droite représentant l'axe des positions horizontales de l'objet en vraie grandeur[4].
Équilibre de l'oscillateur
Modèle:AlAyant écarté l'objet vers la droite et après l'avoir lâché sans vitesse initiale, on observe une oscillation horizontale ;
Modèle:Alle poids de l'objet étant compensé par la réaction du plan horizontal, le mouvement de l'objet ne peut être engendré que par l'action du ressort, action horizontale ; sous cette action, l'objet oscille d'où le nom d'« oscillateur » donné à l'objet relié à un ressort ;
Modèle:Alen pratique les oscillations sont d'amplitude de plus en plus faible à cause des frottements de l'air sur l'objet[5] et elles finissent par disparaître, l'« objet acquérant sa position d'équilibre », la longueur du ressort y étant sa longueur à vide .
Cause de déséquilibre, loi de Hooke

Modèle:AlLe ressort , de longueur à vide et de raideur exprimée en exerce sur point matériel fixé à une extrémité de une force notée ou plus simplement appelée « tension du ressort » s'exerçant sur ;
Modèle:Alavec vecteur unitaire de l'axe de orienté de vers soit encore ,
Modèle:AlModèle:Transparentla tension du ressort s'exerçant sur c.-à-d. s'exprime selon la « loi de Hooke »[6]
Modèle:Encadre
Modèle:AlModèle:Transparentoù est la longueur de à l'instant encore appelée longueur à charge et
Modèle:AlModèle:Transparent l'allongement algébrique par rapport à la longueur à vide ;
Modèle:Alcette loi définit la raideur
du ressort comme le « cœfficient de proportionnalité permettant de passer de la valeur absolue de l'allongement du ressort par rapport à sa longueur à vide à la norme de tension de ce dernier », dans la mesure où on reste dans le domaine d'élasticité du ressort soit :
Modèle:Remarque Modèle:Remarque Modèle:Remarque
Rappel de dynamique, relation fondamentale de la dynamique newtonienne (r.f.d.n.)
Modèle:AlOn décrit le mouvement d'un objet sur un axe en précisant la variation, en fonction du temps, de :
- son « abscisse », variation définissant sa loi horaire de position ,
- sa « vitesse » c.-à-d. la dérivée temporelle 1ère de son abscisse ou loi horaire de vitesse et
- son « accélération » c.-à-d. la dérivée temporelle 2nde de l'abscisse ou dérivée temporelle 1ère de la vitesse ou encore loi horaire d'accélération ;
Modèle:Alle mouvement d'un objet ayant pour cause les forces exercées par son environnement sur lui-même, « la relation fondamentale de la dynamique newtonienne[7] r.f.d.n. énonce le lien existant entre la cause du mouvement et le mouvement dans un certain type de référentiel dit “ galiléen ”[8]Modèle:,[9] »[10] :
Mise en équation
Modèle:AlSur l'objet repéré par son abscisse à partir de sa position d'équilibre sur l'axe horizontal orienté vers la droite par le vecteur unitaire , ne s'exerce qu'une force horizontale « la tension du ressort » appliquée à , , étant égale à l'allongement du ressort , les autres forces poids et réaction du plan horizontal étant verticales et se compensant ;
Modèle:Alappliquant la r.f.d.n.[11] à
et la projetant sur
, on obtient :
ou
Modèle:Alla « forme normalisée »[13] de l'équation différentielle du mouvement de l'oscillateur s'écrit «» ou,
Modèle:AlModèle:Transparenten posant , appelée « pulsation propre de l'oscillateur » exprimée en [14], on obtient sa « forme canonique »
Modèle:AlModèle:Transparent«».
Résolution de l'équation différentielle d'un oscillateur harmonique
Modèle:AlL'équation différentielle du mouvement de l'oscillateur sous forme canonique étant «» est linéaire à cœfficients constants homogène du 2ème ordre en sans terme du 1er ordre, le cœfficient étant égal à et donc selon la notation du paragraphe « cas où le cœfficient du terme d'ordre zéro est strictement positif » chap. de la leçon « Outils mathématiques pour la physique (PCSI) » est de solution sinusoïdale d'où le qualificatif « harmonique »[15] donné à l'oscillateur ;
Modèle:Alla solution s'écrit donc «»[16] ou «», les constantes ou se déterminant à l'aide des C.I.[17] ;
Modèle:Alexemple de C.I.[17] on écarte l'objet de sa position d'équilibre de vers la droite et on le lâche sans vitesse initiale c.-à-d. et :
Modèle:Aldétermination de la loi horaire de position à partir de [16] :
- la forme et la condition initiale d'où ,
- pour écrire la condition de vitesse initiale il faut d'abord exprimer la vitesse pour tout soit et par suite la forme et la condition initiale d'où ,
- finalement la loi horaire de position s'écrit «» et
Modèle:AlModèle:Transparentcelle de vitesseModèle:Transparent«» ;
Modèle:Alremarque détermination de la loi horaire de position à partir de [18] :
Modèle:AlModèle:Transparentla forme et la C.I.[17] d'où ,
Modèle:AlModèle:Transparentcomme précédemment il faut d'abord exprimer la vitesse pour tout soit et par suite la forme et la C.I.[17] d'où c.-à-d. à près,
Modèle:AlModèle:Transparenton choisit alors pour que soit c.-à-d. et par suite ,
Modèle:AlModèle:Transparentfinalement la loi horaire de position s'écrit encore «»[19] et
Modèle:AlModèle:Transparentcelle de vitesseModèle:Transparent«».
Caractéristiques du mouvement
Modèle:AlLa loi horaire de position de l'oscillateur harmonique à C.I.[17] quelconques s'écrit «»[20], « quand il est positif est l'amplitude des oscillations » exprimée en , Modèle:Nobr la phase à l'instant» exprimée en [21], « la phase à l'origine des temps » exprimée en aussi et « la pulsation propre » exprimée en [22] ;
Modèle:Alla fonction « cosinus » étant «
-périodique », la loi horaire de position est
-périodique où «
exprimée en
est la période propre » de l'oscillateur harmonique liée à
par
Modèle:AlModèle:Transparentoù «
est la fréquence propre »
exprimée en
est égale à

Modèle:Alnous représentons ci-contre le diagramme horaire de position de l'oscillateur harmonique dans les C.I.[17] exposées précédemment correspondant à «»[24] ; nous y trouvons aussi le diagramme horaire de vitesse de l'oscillateur harmonique dans les mêmes C.I.[17] correspondant à « » ou, «»[25] en utilisant ;
Modèle:Alcompte-tenu des deux expressions horaires nous dirons que est en « quadrature avance » sur »[26], cela se manifestant par le fait que le diagramme horaire de vitesse passe par un maximum un quart de période avant le diagramme horaire de position, ou qu'il passe par un minimum un quart de période avant le diagramme horaire de position, ou qu'il coupe l'axe des temps en croissant un quart de période avant le diagramme horaire de position
Énergie cinétique, conséquence de l'existence d'un mouvement
Modèle:AlDès lors qu'un objet a un mouvement dans un référentiel donné, il possède un certain type d'énergie dite « cinétique »[27] et
Modèle:AlModèle:Transparentcette énergie est d'autant plus grande que sa vitesse l'est[28] mais aussi que sa masse l'est[28] ;
Modèle:AlModèle:Transparentun objet de masse et de vitesse dans le référentiel d'étude possède l'énergie cinétique [29] ;
Modèle:Alappliqué au mouvement de l'oscillateur harmonique dans les C.I.[17] exposées précédemment
[30] que l'on peut transformer en linéarisant « sinus carré » en utilisant la 3ème forme de
c.-à-d. «
»
dont l'évolution est « sinusoïdale de période [31] autour de sa valeur moyenne égale à »[32] ;
Modèle:Alnous représentons, dans le paragraphe « énergie potentielle élastique, conséquence de l'action d'un ressort » ci-après, le diagramme horaire d'énergie cinétique de l'oscillateur harmonique dans les Modèle:Nobr exposées précédemment courbe en noir.
Énergie potentielle élastique, conséquence de l'action d'un ressort
Modèle:AlDès lors qu'un ressort est étiré ou comprimé, l'objet qui lui est relié possède un certain type d'énergie « potentielle »[33] dite « élastique » et
Modèle:AlModèle:Transparentcette énergie est d'autant plus grande que l'allongement ou la compression du ressort l'est[34] mais aussi que la raideur de ce dernier l'est[34] ;
Modèle:AlModèle:Transparentun ressort de raideur » et d'allongement algébrique relativement à la longueur à vide communique à l'objet l'énergie potentielle élastique [35] ;

Modèle:Alappliqué au mouvement de l'oscillateur harmonique dans les C.I.[17] exposées précédemment où
est aussi l'allongement relativement à la longueur à vide, on en déduit une 1ère expression de
que l'on peut transformer en linéarisant « cosinus carré » selon la 2ème forme de
c.-à-d. «
»
d'où
Modèle:Alnous représentons, ci-contre, le diagramme horaire d'énergie potentielle élastique de l'oscillateur harmonique dans les C.I.[17] exposées précédemment courbe en rouge.
Définition de l'énergie mécanique et sa conservation, conséquence de l'absence de forces autres que celle du ressort
Modèle:AlL'oscillateur harmonique dans n'importe quelles C.I.[17] possède de l'énergie cinétique due à son mouvement dans le référentiel d'étude et
Modèle:AlModèle:Transparentde l'énergie potentielle élastique due à sa liaison avec un ressort,
Modèle:AlModèle:Transparentil possède donc au total l'énergie dite « mécanique »[37] «» ;
Modèle:Alutilisant les expressions de
et de
en fonction de
, obtenues pour les C.I.[17] exposées plus haut, nous obtenons «
» soit, après simplification évidente
l'énergie mécanique reste constante et égale à l'énergie mécanique initiale
«» ;
Modèle:Alnous vérifions, sur cet exemple, que l'énergie mécanique initialement créée est conservée en absence de frottements[38].
Modèle:AlNous pourrons appliquer la conservation de l'énergie mécanique dès lors que les forces autres que la tension du ressort c.-à-d. le poids et la réaction du plan horizontal n'ont aucune action sur le mouvement donc aucune action de freinage entre autres et l'utilisation de la conservation de l'énergie mécanique peut remplacer l'application de la r.f.d.n.[11] ;
Modèle:Alnous obtenons alors «» c.-à-d. une équation différentielle non linéaire du 1er ordre en , encore appelée « intégrale 1ère du mouvement » dans la mesure où elle pourrait être obtenue par une 1ère intégration de l'équation différentielle du 2ème ordre[39].
Modèle:AlOn peut se servir de la conservation de l'énergie mécanique pour trouver la vitesse de connaissant sa position ou pour trouver sa position connaissant sa vitesse et ceci sans aucune information sur l'instant d'observation.
Retrouver l'équation différentielle du mouvement à partir de la conservation de l'énergie mécanique
Modèle:AlOn retrouve l'équation différentielle du mouvement en à partir de l'intégrale 1ère du mouvement associée à la conservation de l'énergie mécanique « », pour cela on dérive cette dernière relativement au temps [40], en utilisant [41] «» que l'on réécrit encore selon «» ;
Modèle:Alau final on obtient : «»[42] ou, en mettant en facteur après simplification évidente, «» ;
Modèle:Alon en déduit l'équation différentielle du mouvement cherchée «» car la nullité de l'autre facteur c.-à-d. correspondant à l'absence de mouvement est à rejeter.
Notes et références
- ↑ De façon à ce que le ressort puisse aussi se comprimer sans obstacle.
- ↑ Son allongement ou sa compression sous une action extérieure doit être tel qu'il reprenne sa longueur initiale dite à vide quand l'action extérieure cesse.
- ↑ La raideur d'un ressort étant définie dans le paragraphe « cause de déséquilibre, loi de Hooke » plus loin dans ce chapitre.
- ↑ Dans le schéma ci-dessus il y a volontairement une erreur de perspective de façon à le rendre plus lisible, en fait l'axe horizontal du ressort est aux axes des rouleaux entraînant le papier enregistreur, tous ces axes devant donc être au plan de front, le stylet, quant à lui, lui étant , c'est ce que sous-entend la courbe tracée sur la feuille d'enregistrement ;
Modèle:Alen fait la partie du schéma constituée du ressort ne doit pas être vue comme faisant partie de la perspective mais comme une vue « projetée sur un axe horizontal », ceci constituant une erreur « volontaire » de perspective que l'on aurait pu éviter en inclinant l'axe du ressort parallèlement aux axes des rouleaux engendrant le défilement du papier enregistreur - ↑ Il y a aussi les frottements de glissement de l'objet sur le plan horizontal ; pour les rendre les plus faibles possibles en effet leur présence peut entraîner une position d'équilibre différente de celle précisée dans ce paragraphe on peut faire glisser l'objet sur de l'huile ou comme c'est suggéré dans le mode opératoire du paragraphe « description » plus haut dans ce chapitre sur un coussin d'air.
- ↑ Robert Hooke (1635 - 1703) est l'un des plus grands scientifiques expérimentaux anglais du XVIIème siècle ayant contribué à l'avancement des sciences et techniques dans pratiquement tous les domaines.
- ↑ Construit à partir du nom de Newton ;
Modèle:AlIsaac Newton (1643 - 1727) philosophe, mathématicien, physicien, astronome, alchimiste et théologien anglais, connu essentiellement de nos jours pour avoir fondé la mécanique classique, pour sa théorie de la gravitation et aussi pour la création du calcul infinitésimal ; en optique il a développé une théorie de la couleur et a aussi inventé un télescope composé d'un miroir primaire concave et d'un miroir secondaire plan, télescope connu de nos jours sous le nom de télescope de Newton. - ↑ Construit à partir du nom de Galilée ;
Modèle:AlGalileo Galilei (1564 - 1642) mathématicien, géomètre, physicien et astronome italien plus exactement pour l'époque florentin, à qui on doit en l'amélioration de la longue vue inventée par l'opticien hollandais Hans Lippershey (1570 - 1619) en lunette d'observation des objets célestes sans inversion de l'image par ajout d'une lentille divergente ; dès en observant les phases de Vénus, il est convaincu que le géocentrisme ne permet pas une explication simple de cette observation contrairement à l'héliocentrisme théorie physique dont l'essor est essentiellement dû à Nicolas Copernic (1473 - 1543) chanoine, médecin et astronome polonais et défend cette thèse en poursuivant ses observations jusqu'en où il fût déclaré suspect d'hérésie par l'Inquisition romaine et dût adjurer ; il a aussi posé les bases de la mécanique en étudiant l'équilibre et le mouvement des corps solides en particulier leur chute, leur translation rectiligne et leur inertie ainsi que la généralisation des mesures de temps en particulier par l'étude de l'isochronisme du pendule. - ↑ Voir le paragraphe « référentiels galiléens » du chap. de la leçon « Mécanique 1 (PCSI) ».
- ↑ Voir le paragraphe « autre forme de la relation fondamentale spécifique à la dynamique newtonienne, la “ r.f.d.n. ” (forme la plus usitée de la relation fondamentale de la dynamique newtonienne) » du chap. de la leçon « Mécanique 1 (PCSI) ».
- ↑ 11,0 et 11,1 Relation Fondamentale de la Dynamique Newtonienne.
- ↑ C.-à-d. une équation différentielle linéaire à cœfficients constants du 2nd ordre homogène sans terme du 1er ordre.
- ↑ Définie avec le cœfficient de la dérivée de plus haut ordre égal à et s'obtenant quand ce n'est pas le cas en divisant les deux membres par le cœfficient de la dérivée de plus haut ordre.
- ↑ On dit alors que l'on fait une « réduction canonique du problème » ; faire une réduction canonique c'est éliminer les grandeurs spécifiques au problème pour les remplacer par des grandeurs qui vont caractériser le type de problème ; par exemple si on multiplie la raideur par et que l'on fait de même pour la masse , on aura la même pulsation propre donc le même mouvement ; un autre intérêt de faire une réduction canonique d'un problème est que l'on peut trouver un problème équivalent dans un autre domaine de la mécanique ou plus généralement de la physique.
- ↑ Harmonique étant synonyme de sinusoïdal.
- ↑ 16,0 et 16,1 Choix à privilégier si l'abscisse ou la vitesse est nulle à l'instant initial
- ↑ 17,00 17,01 17,02 17,03 17,04 17,05 17,06 17,07 17,08 17,09 17,10 et 17,11 Condition(s) Initiale(s).
- ↑ D'après ce qui a été dit précédemment ce choix est maladroit, mais il n'est pas interdit.
- ↑ Le choix de implique ne représente donc pas l'amplitude des oscillations et la loi horaire de position s'écrit «» que l'on transforme en Modèle:Nobr » compte-tenu de .
- ↑ Usuellement on note le cœfficient de au lieu de .
- ↑ Rappel de la définition du « radian » unité mathématique et non physique ne doit pas être considérée pour vérifier l'homogénéité des formules : mesure d'un angle au centre telle que la longueur de l'arc qu'il délimite sur un cercle est égale au rayon du cercle ou avec si .
- ↑ Nous avons posé en précisant que son unité déduite de l'équation différentielle est c'est aussi en accord avec le fait que le ne pouvait être trouvé par des considérations d'homogénéité de l'équation différentielle.
- ↑ En effet, quand augmente de , augmente de d'où .
- ↑ C'est aussi ce qu'on observerait sur l'enregistrement du dispositif expérimental du début de chapitre aux amortissements près en effet les frottements, mêmes réduits au minimum, sont inévitables ceci se manifeste par un très léger amortissement exponentiel dans la mesure où les frottements fluides prédominent.
- ↑ On remarque que, pour dériver par rapport au temps, une grandeur sinusoïdale du temps il suffit de multiplier l'amplitude par et ajouter à la phase à l'origine soit .
- ↑ Si et , on dit que est en quadrature avance sur si , étant par conséquent en quadrature retard sur .
- ↑ L'énergie cinétique sera notée , on peut encore trouver ou, plus rarement, mais ici ce serait très mal venu, représentant déjà la projection de la tension du ressort sur , toutefois je privilégierai la notation .
- ↑ 28,0 et 28,1 L'énergie cinétique varie de façon quadratique avec la vitesse c.-à-d. proportionnellement au carré de la vitesse et linéairement avec la masse.
- ↑ Cette expression a été introduite au cours du secondaire et sera revue au paragraphe « définition de l'énergie cinétique d'un point matériel dans le référentiel d'étude à partir des grandeurs d'inertie et cinématique du point » du chap. de la leçon « Mécanique 1 (PCSI) ».
- ↑ Cette dernière forme étant obtenue en utilisant .
- ↑ La pulsation d'oscillation de étant double de cette de , la période est donc la moitié.
- ↑ 32,0 et 32,1 La valeur moyenne d'une grandeur est notée ou simplement , sa définition sera vue en note « 4 » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » ;
Modèle:Alici il suffit de savoir que sur un intervalle d'une période de , soit , à chaque valeur de , on peut associer une valeur unique de telle que en effet d'où la valeur moyenne d'un cosinus sur un intervalle d'une période est nulle soit ou, avec , et
Modèle:AlModèle:Transparentque la valeur moyenne d'une constante est la constante soit . - ↑ L'énergie potentielle sera notée , on peut encore trouver , toutefois je privilégierai la notation .
- ↑ 34,0 et 34,1 L'énergie potentielle élastique varie de façon quadratique avec l'allongement algébrique c.-à-d. proportionnellement au carré de l'allongement algébrique et linéairement avec la raideur.
- ↑ Cette expression sera établie sous une forme plus générale au paragraphe « énergie potentielle élastique d'un point matériel » du chap. de la leçon « Mécanique 1 (PCSI) ».
- ↑ La pulsation d'oscillation de étant double de cette de , la période est donc la moitié.
- ↑ Voir le paragraphe « définition de l'énergie mécanique d'un point matériel dans un champ de force(s) conservative(s) » du chap. de la leçon « Mécanique 1 (PCSI) ».
- ↑ Nous démontrerons dans le paragraphe « 1ère justification du signe “ - ” dans la définition de l'énergie potentielle du mouvement d'un point matériel dans un champ de force(s) conservative(s) par réécriture du théorème de l'énergie cinétique » du chap. de la leçon « Mécanique 1 (PCSI) » à partir de l'application de la r.f.d.n.
Modèle:AlModèle:Transparentle « théorème de la variation de l'énergie mécanique d'un point matériel dans un champ de force(s) conservative(s) » énoncé dans le même chap. de la même leçon « Mécanique 1 (PCSI) » la notion de force conservative ou non étant vue dans les paragraphes « 1ère définition d'une force conservative » et « exemples de forces non conservatives » de ce chap. de la leçon « Mécanique 1 (PCSI) » et son cas particulier,
Modèle:AlModèle:Transparentla « conservation de l'énergie mécanique d'un point matériel “ à mouvement conservatif ” » énoncée dans le chap. de la leçon « Mécanique 1 (PCSI) » mais
Modèle:AlModèle:Transparentpour l'instant nous nous contentons d'une simple vérification. - ↑ Ce n'est pas parce que l'équation différentielle trouvée par conservation de l'énergie mécanique est d'ordre un qu'elle est plus simple à intégrer que celle du mouvement trouvée par application de la r.f.d.n. qui est d'ordre deux ; ce qui compte pour la simplicité de l'intégration est le caractère linéaire de l'équation différentielle et dans ce cas c'est indéniablement l'équation différentielle du mouvement d'ordre deux qui est la plus simple.
- ↑ La dérivation d'une équation différentielle du 1er ordre augmentant l'ordre de l'équation différentielle d'une unité, nous obtiendrons effectivement une équation différentielle du 2ème ordre.
- ↑ On adopte ici la notation « différentielle » pour écrire la dérivée, ce qui permet de retenir plus facilement la formule de dérivation d'une fonction composée ; pour dériver la fonction composée par rapport à la variable , on dérive la fonction relativement à la variable intermédiaire et on multiplie par la dérivée de la fonction relativement à la variable .
- ↑ La dérivée de la constante par rapport au temps étant nulle.