Signaux physiques (PCSI)/Optique géométrique : l'œil
Modélisation de l'œil comme association d'une « pseudo-lentille » de vergence variable et d'un capteur fixe
Description sommaire de l'œil
Modèle:AlL'œil humain est un système optique complexe puisqu’il comporte une succession de dioptres qui ne sont pas parfaitement sphériques et que ses milieux extrêmes sont différents ;
Modèle:Alun œil se présente comme un globe, de de diamètre environ, limité par une membrane résistante, « la sclérotique ».
-
Coupe d'un œil humain
Modèle:AlOn distingue principalement, comme le montre la figure ci-dessus :
- « la cornée », partie antérieure de la sclérotique, transparente, d'indice ,
- « l'humeur aqueuse », liquide transparent d'indice ,
- « le cristallin », lentille biconvexe élastique d'indice [1],
- « l'humeur vitreuse », liquide gélatineux d'indice et
- « la rétine », membrane sensible aux radiations lumineuses, située au fond de l’œil.
Modèle:AlLa rétine a une structure « discontinue » formée de cellules coniques les « cônes », de cellules cylindriques « les bâtonnets » et de cellules nerveuses les « neurones » ;
- les 1ères les cônes, concentrées au centre de la rétine, sont surtout excitées en « vision diurne », dite « photopique » ; elles sont de trois types « les rouges, les verts et les bleus » [2] et sont au nombre d'environ millions par œil, elles permettent de distinguer jusqu'à couleurs [3] ; leurs tailles varient entre et , autour d’une valeur moyenne de environ ;
- les 2ndes les bâtonnets, localisées sur le pourtour de la rétine, sont surtout stimulées en « vision nocturne », dite « scotopique » ; sensibles à l'éclairement et non aux couleurs, elles sont au nombre d'environ millions par œil ; leur taille correspond à une longueur de en moyenne.
Modèle:Al« La sensibilité de la rétine est maximale sur un petit cercle voisin de l’axe », de rayon , appelé « tache jaune » ou « macula » ;
Modèle:Alil existe aussi une « tache aveugle ou papille », zone où les fibres nerveuses de la rétine se réunissent pour former le « nerf optique » [4] et qui ne renferme aucune cellule photosensible ;
Modèle:Alenfin une petite zone « la fovéa » dépourvue de bâtonnets est particulièrement sensible aux couleurs, elle est pratiquement confondue avec la « macula » ; la « fovéa » est donc la zone la plus sensible en journée mais « la moins sensible la nuit » [5].
Modèle:AlLa « sensibilité de la rétine dépend de la nature spectrale du rayonnement » [6] :
Modèle:Alci-dessous à gauche la comparaison de la sensibilité spectrale normalisée des trois types de cônes[7] et des bâtonnets :
Modèle:AlCi-dessous à droite la comparaison de la sensibilité spectrale normalisée de l'ensemble des cônes utilisé en vision diurne ou photopique et des bâtonnets en vision nocturne ou scotopique.
-
Comparaison des courbes de sensibilités relatives en visions photopique et scotopique
Modèle:AlEn avant du cristallin, un diaphragme, appelé « pupille », limite la quantité de lumière incidente à celle nécessaire à la détection. Grâce à une membrane, « l'iris », diversement colorée, le diamètre de la pupille peut varier entre et [8].
Modélisation de l'œil en association d'une « pseudo-lentille » de vergence variable et d'un capteur fixe
Modèle:AlOn peut modéliser l'œil en « 1ère approximation » par « l'œil réduit de Listing »[9] c.-à-d. l'association d'une « pseudo lentille »[10] sphérique de vergence variable « le cristallin » [11] et d'un capteur fixe « la rétine » ; pour affiner on ajoute la présence d'un diaphragme « la pupille » situé légèrement en deçà de la pseudo lentille[10].
Propriété de la « pseudo-lentille » de vergence variable modélisant les dioptres sphériques successifs et le cristallin
Modèle:AlLe cristallin est constitué d'un assemblage ordonné de cellules ; son centre est formé de cellules « mortes » en forme de prisme qui contiennent en grande quantité une protéine « la cristalline », responsable de la forte vergence du cristallin ; une mince couche faite de cellules « vivantes » cubiques recouvre le centre du cristallin et sont responsables de la croissance du cristallin ;
Modèle:Alle cristallin peut, grâce à de petits muscles, changer de vergence, cette propriété est essentielle pour obtenir des objets localisés à une distance variable du cristallin une image nette sur la rétine fixe relativement à ce dernier ;
Modèle:Alpour faire « converger fortement la lumière » [12], le cristallin se bombe, ainsi sa vergence vergence maximale de la « pseudo lentille[10] équivalente aux dioptres sphériques successifs et au cristallin bombé » [13]Modèle:,[14] et la distance focale image de la pseudo lentille[10] la distance focale image minimale du dioptre sphérique modélisé par la pseudo lentille[10] étant finalement [14] ;
Modèle:Alpour faire « converger faiblement la lumière »[15], le cristallin s'amincit, ainsi sa vergence vergence minimale de la « pseudo lentille[10] équivalente aux dioptres sphériques successifs et au cristallin non bombé » [13]Modèle:,[14] et la distance focale image de la pseudo lentille[10] la distance focale image maximale du dioptre sphérique modélisé par la pseudo lentille[10] étant [14] ;
Modèle:Alcette capacité de l'œil à faire varier la vergence du cristallin selon les situations est appelée « accommodation ».
Modèle:AlUn œil « normal » [16] est qualifié d'« emmétrope », le contraire étant « amétrope ».
Plage d'accommodation de l'œil
Œil emmétrope n'accommodant pas et punctum remotum ou PR de cet œil
Modèle:AlUn œil « emmétrope »[17] est dit « n'accommodant pas » quand il est dans la situation où le cristallin a son amincissement maximal,
Modèle:AlModèle:Transparentil donne alors d’un objet situé à l’infini une image nette sur la rétine située à une distance moyenne du cristallin de[18],
Modèle:AlModèle:Transparentla « rétine étant dans le plan focal image du dioptre sphérique modélisant l'œil » [19]Modèle:,[20] ou,
Modèle:Alpour rester dans le cadre de la pseudo lentille[10], correspondant à une distance focale image de cette dernière c.-à-d.
Modèle:AlModèle:Transparentune vergence de cette dernière ou du dioptre sphérique équivalent [13] ;
Modèle:Alquand l'« œil n'accommode pas » on dit encore que l'objet est situé au « punctum remotum ou PR » de l'œil[21].
Œil emmétrope accommodant au maximum et punctum proximum ou PP de cet œil
Modèle:AlUn œil « emmétrope »[17] est dit « accommodant au maximum » quand il est dans la situation où le cristallin se déforme au maximum
Modèle:AlModèle:Transparentla rétine étant toujours située à la distance moyenne de du cristallin bombé[18]
Modèle:AlModèle:Transparentil donne alors une image nette d'un objet linéique transverse[22] situé à la distance minimale de vision distincte[23] de valeur moyenne [24],
Modèle:AlModèle:Transparentla rétine devient alors le plan conjugué par le dioptre sphérique équivalent ou par la pseudo lentille[10]de celui contenant l'objet[20],
Modèle:AlModèle:Transparentla vergence du dioptre sphérique équivalent ou de la pseudo lentille[10] accommodant au maximum étant [13]Modèle:,[25] correspondant à
Modèle:AlModèle:Transparentune distance focale image de la pseudo lentille[10] ou
Modèle:AlModèle:Transparentdu dioptre sphérique équivalent , positionnant la rétine au-delà du plan focal image de ce dernier quand le cristallin est déformé au maximum[26] ;
Modèle:Alquand l'« œil accommode au maximum » on dit encore que l'objet est situé au « punctum proximum ou PP » de l'œil.
Coupe du modèle de Listing d'un œil emmétrope
-
Coupe du modèle de Listing[9] d'un œil emmétrope avec position en rouge de son foyer principal image sans accommodation associée à son PR et position en bleu de son foyer principal image avec accommodation maximale associée à son PP
Modèle:AlCi-dessus une coupe du modèle de Listing[9] d'un œil emmétrope utilisant le dioptre sphérique équivalent[27], le schéma n'étant pas fait à l'échelle :
- en rouge on suppose que l'œil emmétrope n'accommode pas,
Modèle:Transparentle foyer principal image du dioptre sphérique équivalent , centré sur la rétine[28], est l'image du PR de l'œil, situé à l'infini sur l'axe optique principal,
Modèle:Transparentle foyer principal objet non représenté serait situé en deçà du sommet du dioptre sphérique équivalent ou de la pseudo lentille[10]Modèle:,[29]Modèle:,[30] ; - en bleu on suppose que l'œil emmétrope accommode au maximum,
Modèle:Transparentle foyer principal image du dioptre sphérique équivalent , situé en deçà de la rétine[31], est l'image du PP de l'œil, situé à sur l'axe optique principal en deçà du sommet du dioptre sphérique équivalent,
Modèle:Transparentle foyer principal objet non représenté serait situé en deçà du sommet du dioptre sphérique équivalent ou de la pseudo lentille[10]Modèle:,[29]Modèle:,[32].
Limite de résolution angulaire de l'œil
Condition pour que deux images ponctuelles sur la rétine soient séparées
Modèle:AlLa structure granulaire limite la capacité de l’œil à distinguer des détails. En effet, si la distance de deux images ponctuelles sur la rétine est trop faible, une seule cellule est impressionnée et le cerveau ne fait aucune différence entre ces deux points.
Modèle:Al« Pour une séparation des points objet faite sans ambiguïté, il faut que les images ponctuelles correspondantes se forment sur deux cellules séparées par une 3ème »
Modèle:AlModèle:Transparentce qui correspond, en notant « le diamètre d'une cellule », et
Modèle:AlModèle:Transparenten supposant « les images ponctuelles centrées sur les cellules qu'elles impressionnent »,
Modèle:AlModèle:Transparentà une « distance séparant les images ponctuelles correspondantes de» ;
Modèle:Alnous adoptons donc le critère moyen[33] suivant de séparation des points image sur la rétine :
Modèle:Alen conclusion : si « la distance séparant les points image sur la rétine est à », les points image impressionnent la même cellule ou deux cellules voisines et ils ne sont pas séparables et
Modèle:AlModèle:Transparent à », les points image impressionnent deux cellules séparées par au moins une 3ème et ils sont séparables.
Axes optiques secondaires de l'œil de Listing
Modèle:AlUn axe optique secondaire de l'œil de Listing[9] est l'association
- d'un rayon incident passant par le sommet du dioptre sphérique équivalent ou par le centre optique de la pseudo lentille[10] incliné d'un angle par rapport à l'axe optique principal et
- du rayon émergent associé, incliné d'un angle par rapport à l'axe optique principal ,
Modèle:AlModèle:Transparentles deux angles d'inclinaison obéissant à la 2ème loi de Snell - Descartes[34] de la réfraction[35] appliquée aux petits angles[36] soit « avec » ;
-
Coupe du modèle de Listing[9] d'un œil emmétrope avec axe optique secondaire, position en rouge de son foyer secondaire image sans accommodation associée à son PR, position en bleu de son foyer secondaire image avec accommodation maximale associée à son PP
Modèle:Alci-dessus « l'axe optique secondaire représenté est écarté de l'angle minimal par rapport à l'axe optique principal » tel que « les impacts sur la rétine de et de sont séparés de »[37],
Modèle:AlModèle:Transparent« condition minimale de séparation des deux images ponctuelles ».
Notion de limite de résolution angulaire de l'œil
Modèle:AlLa « limite de résolution angulaire de l'œil est la valeur minimale de , angle entre un axe optique secondaire et l'axe optique principal[38] pour que les deux impacts sur la rétine soient séparables »[39].
Modèle:AlSachant que le « diamètre moyen d'un cône est », on en déduit «»[40], et par suite
Modèle:AlModèle:Transparentla « limite de résolution angulaire de l'œil
Modèle:AlModèle:Transparent» ;
Distance angulaire minimale entre deux étoiles permettant de les distinguer à l'œil nu
Modèle:AlLa « distance angulaire minimale entre deux étoiles permettant de les distinguer à l'œil nu est, par définition, la limite de résolution angulaire de l'œil soit »[41] ;
Modèle:Alon peut soi-même de façon très élémentaire vérifier l’ordre de grandeur de cette distance angulaire minimale ou de la limite de résolution angulaire de l'œil
Modèle:AlModèle:Transparenten divisant le diamètre apparent[43] de la Lune ,
Modèle:AlModèle:Transparentpar le nombre d’éléments une vingtaine
Modèle:AlModèle:Transparentque l’on peut distinguer sur l’un de ses diamètres.
Distance minimale séparant deux points placés au PP de l'œil pour les distinguer à l'œil nu
Modèle:Al« Deux points objet situés au PP de l'œil sont séparables si leur distance mutuelle est à »[44] où « est la distance minimale de vision distincte »[24] c.-à-d.
Modèle:AlModèle:Transparentpour une « distance mutuelle minimale de en [45] donnant » ;
Compléments, principaux défauts de l'œil
Modèle:AlIl existe plusieurs défauts bien connus de l’œil, appelés « amétropies ». Les plus répandus sont la « myopie », l’« hypermétropie », la « presbytie » et l’« astigmatisme ».
La myopie

Modèle:AlUn œil « myope » est « trop convergent ou trop profond » [48] ;
Modèle:Alquel que soit le type de myopie, quand l'œil n'accommode pas, « un faisceau à l'axe optique principal converge en un point image situé en deçà de la rétine » [49] établissant que le punctum remotum PR d'un œil myope n'est pas le point à l'infini de mais un point réel de à distance finie du sommet du dioptre sphérique équivalent ou encore à distance finie du centre optique de la pseudo lentille[10][50] voir schéma ci-contre ; de même
Modèle:AlModèle:Transparentquand un œil myope accommode au maximum, son punctum proximum PP est situé plus près du sommet du dioptre sphérique équivalent ou encore plus près du centre optique de la pseudo lentille[10] que celui d'un œil emmétrope c.-à-d. normal[51], schéma de situation non représenté.
L'hypermétropie

Modèle:AlUn œil « hypermétrope » est « à convergence trop faible ou
Modèle:AlModèle:Transparenttrop courte » ;
Modèle:Alquel que soit le type d'hypermétropie, quand l'œil n'accommode pas, un faisceau à l'axe optique principal converge en un point image situé au-delà de la rétine[52] établissant que le punctum remotum PR d'un œil hypermétrope n'est pas le point à l'infini de mais un point virtuel de à distance finie au-delà du sommet du dioptre sphérique équivalent ou à distance finie au-delà du centre optique de la pseudo lentille[10][53] voir schéma ci-contre ; de même
Modèle:AlModèle:Transparentquand un œil hypermétrope accommode au maximum, son punctum proximum PP est situé plus éloigné du sommet du dioptre sphérique équivalent ou encore plus éloigné du centre optique de la Modèle:Nobr quel que soit le type d'hypermétropie, que celui d'un œil emmétrope c.-à-d. normal[54], schéma de situation non représenté.
Correction de la myopie et de l'hypermétropie
Modèle:AlOn corrige ces défauts à l’aide de verres ou de lentilles cornéennes voir figures ci-dessous,
- « divergents si l’œil est myope » et
- « convergents si l’œil est hypermétrope »
Correction de la myopie
-
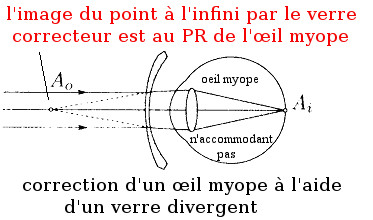
Correction d'un œil myope n'accommodant pas avec un verre divergent conjuguant le point à l'infini et le punctum remotum PR de l'œil myope
Modèle:AlCorrection d'un œil myope n'accommodant pas avec un verre divergent voir la figure ci-dessus :
Modèle:AlModèle:Transparentdans le cas où la myopie est due à une vergence trop grande de l'œil n'accommodant pas Modèle:Nobr »[13],
Modèle:AlModèle:Transparentsi on accole à l'œil myope une lentille divergente de vergence , la vergence de l'œil myope corrigé n'accommodant pas, égale à Modèle:Nobr », est celle d'un œil emmétrope n'accommodant pas si « »[55] ;
Modèle:AlModèle:Transparentdans le cas où la myopie est due à une trop grande profondeur de l'œil,
Modèle:AlModèle:Transparentla vergence de l'œil myope n'accommodant pas étant «»[13] «» mais
Modèle:AlModèle:Transparentla profondeur de l'œil « étant telle que » empêchant le PR de l'œil myope d'être à l'infini, il convient,
Modèle:AlModèle:Transparentpour que le PR de l'œil myope corrigé soit à l'infini, d' la distance focale image sans accommoder
Modèle:Transparentou de la vergence sans accommoder de ce dernier,
Modèle:AlModèle:Transparentce qui se fait encore en accolant une lentille divergente de vergence , telle que « » dont on tire « car » soit finalement
Modèle:AlModèle:Transparent« »[56].
Modèle:AlRemarque : L'ajout d'une lentille divergente accolée à un œil myope permettant de renvoyer le PR à l'infini,
Modèle:AlModèle:Transparenta aussi une action sur le PP de ce dernier lequel, sans lentille additionnelle, est plus proche que celui d'un œil emmétrope.
Modèle:AlCorrection d'un œil myope accommodant au maximum avec un verre divergent figure non représentée :
Modèle:AlModèle:Transparentdans le cas où la myopie est due à une vergence trop grande de l'œil accommodant au maximum « »[13],
Modèle:AlModèle:Transparentsi on accole à l'œil myope la même lentille divergente que précédemment de vergence «», la vergence de l'œil myope corrigé accommodant au maximum, égale à «», serait celle d'un œil emmétrope accommodant au maximum si «»[57] ;
Modèle:AlModèle:Transparentdans le cas où la myopie est due à une trop grande profondeur de l'œil,
Modèle:AlModèle:Transparentla vergence de l'œil myope accommodant au maximum étant « »[13] et
Modèle:AlModèle:Transparentla profondeur de l'œil «» rapprochant le PP de l'œil myope de ce dernier relativement à un œil emmétrope Modèle:Nobr PP étant le conjugué par le dioptre sphérique équivalent ou par la pseudo lentille[10] du point de la rétine sur l'axe optique principal soit «», il convient,
Modèle:AlModèle:Transparentpour que le PP de l'œil myope corrigé soit au même endroit que le PP d'un œil emmétrope,
Modèle:AlModèle:Transparentd' la distance focale image avec accommodation maximale
Modèle:Transparentou de la vergence avec accommodation maximale de ce dernier,
Modèle:AlModèle:Transparentce qui se fait encore en accolant une lentille divergente de vergence , telle que « » dont on tire «» car les vergences de l'œil myope corrigé ou non accommodant au maximum sont égales à d'où, avec , «» soit finalement
Modèle:AlModèle:Transparent«»[58].
Correction de l'hypermétropie
-
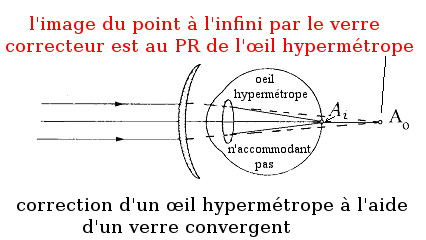
Correction d'un œil hypermétrope n'accommodant pas avec un verre convergent conjuguant le point à l'infini et le punctum remotum PR de l'œil hypermétrope
Modèle:AlCorrection d'un œil hypermétrope n'accommodant pas avec un verre convergent voir la figure ci-dessus :
Modèle:AlModèle:Transparentdans le cas où l'hypermétropie est due à une vergence trop faible de l'œil n'accommodant pas Modèle:Nobr »[13],
Modèle:AlModèle:Transparentsi on accole à l'œil hypermétrope une lentille convergente de vergence , la vergence de l'œil hypermétrope corrigé n'accommodant pas, égale à Modèle:Nobr », est celle d'un œil emmétrope n'accommodant pas si « »[59] ;
Modèle:AlModèle:Transparentdans le cas où l'hypermétropie est due à une trop faible profondeur de l'œil,
Modèle:AlModèle:Transparentla vergence de l'œil hypermétrope n'accommodant pas étant «»[13] d'où
Modèle:AlModèle:Transparent«» mais
Modèle:AlModèle:Transparentla profondeur de l'œil « étant » empêchant le PR de l'œil hypermétrope d'être à l', il convient,
Modèle:AlModèle:Transparentpour que le PR de l'œil hypermétrope corrigé soit à l'infini, de la distance focale image sans accommoder
Modèle:AlModèle:Transparentou d' la vergence sans accommoder de ce dernier,
Modèle:AlModèle:Transparentce qui se fait encore en accolant une lentille convergente de vergence , telle que «» dont on tire « car » conduisant effectivement à soit finalement
Modèle:AlModèle:Transparent« »[60].
Modèle:AlRemarque : L'ajout d'une lentille convergente accolée à un œil hypermétrope permettant de fixer le PR à l'infini,
Modèle:AlModèle:Transparenta aussi une action sur le PP de ce dernier lequel, sans lentille additionnelle, est plus éloigné que celui d'un œil emmétrope.
Modèle:AlCorrection d'un œil hypermétrope accommodant au maximum avec un verre convergent figure non représentée :
Modèle:AlModèle:Transparentdans le cas où l'hypermétropie est due à une vergence trop faible de l'œil accommodant au maximum
Modèle:AlModèle:Transparent«»[13],
Modèle:AlModèle:Transparentsi on accole à l'œil hypermétrope la même lentille convergente que précédemment de vergence « », la vergence de l'œil hypermétrope corrigé accommodant au maximum, égale à «», serait celle d'un œil emmétrope accommodant au maximum si «»[61] ;
Modèle:AlModèle:Transparentdans le cas où l'hypermétropie est due à une trop faible profondeur de l'œil,
Modèle:AlModèle:Transparentla vergence de l'œil hypermétrope accommodant au maximum étant « »[13] et
Modèle:AlModèle:Transparentla profondeur de l'œil «» éloignant le PP de l'œil hypermétrope de ce dernier relativement à un œil emmétrope Modèle:Nobr PP étant le conjugué par le dioptre sphérique équivalent ou par la pseudo lentille[10] du point de la rétine sur l'axe optique principal soit «»,
Modèle:AlModèle:Transparentil convient, pour que le PP de l'œil hypermétrope corrigé soit au même endroit que le PP d'un œil emmétrope,
Modèle:AlModèle:Transparentde la distance focale image avec accommodation maximale
Modèle:Transparentou d' la vergence avec accommodation maximale de ce dernier,
Modèle:AlModèle:Transparentce qui se fait encore en accolant une lentille convergente de vergence , telle que « » «» car les vergences de l'œil hypermétrope corrigé ou non accommodant au maximum sont d'où, avec , «» soit finalement
Modèle:AlModèle:Transparent«»[62].
La presbytie
Modèle:AlLa presbytie est le défaut d’accommodation d’un œil ; elle se manifeste par un rapprochement du punctum proximum (PP) du punctum remotum la position du PR restant usuellement inchangée ;
Modèle:Alce défaut peut affecter toutes les vues avec l'âge, il est usuellement rectifié à l’aide de verres à correction progressive, la partie supérieure du verre permettant la vision éloignée si besoin est et
Modèle:AlModèle:Transparentla partie inférieure Modèle:Transparentla vision proche :
- pour un œil emmétrope devenu presbyte, les verres sont pratiquement afocaux en vision éloignée et
Modèle:Transparentconvergents en vision proche, - pour un œil myope devenu presbyte, les verres sont fortement divergents pour voir de loin et
Modèle:Transparentfaiblement divergents pour voir de près et enfin - pour un œil hypermétrope devenu presbyte, les verres sont faiblement convergents pour voir de loin et
Modèle:Transparentfortement convergents pour voir de près.
L'astigmatisme
Modèle:AlL’astigmatisme d’un œil est « la différence de focalisation de deux objets linéiques transverses[22] de directions »[63] ;
Modèle:Alon attribue l'astigmatisme au défaut de symétrie de révolution de la cornée ;
Modèle:Alon compense cet astigmatisme à l’aide de verres eux-mêmes astigmatiques.
Corrections actualisées des défauts de l'œil
Modèle:AlDe nos jours, on cherche à corriger les défauts de l’œil, notamment la myopie et l’astigmatisme, par modification de la géométrie de la surface de la cornée ;
Modèle:Alavec un « laser à excimère »[64] ou un « laser à exciplexe » [65], on réalise une « photoablation » [66] d’une partie de la cornée, ce qui modifie sa courbure et donc sa vergence.
Notes et références
- ↑ La perte accidentelle ou par vieillesse de transparence du cristallin s'appelle « la cataracte ».
- ↑ Et vraisemblablement un 4ème type chez des hommes et des femmes « les oranges ».
Modèle:AlLe dysfonctionnement d'un des trois types de cônes est le « daltonisme » et celui des trois types l'« achromatopsie ». - ↑ En proportion plus grande dans les nuances de vert et de rouge que celles de bleu.
- ↑ Conduisant les informations visuelles jusqu'au cerveau.
- ↑ En conséquence on voit mieux les objets en « vision périphérique » la nuit qu'en « vision axiale », fixer les objets la nuit n'est donc pas la bonne façon pour les distinguer.
- ↑ La sensibilité de la rétine progressivement dans l'obscurité, elle atteint une accoutumance maximale au bout d'une heure mais cette adaptation disparaît très rapidement au moindre éblouissement, avec la nécessité d'une même durée pour la retrouver.
- ↑ Les cônes rouges ayant une sensibilité maximale approximativement fois plus grande que celle des cônes verts et approximativement fois plus grande que celle des bleus.
- ↑ La dimension maximale de la pupille est affectée par la vieillesse d'où le besoin d'un éclairage plus intense pour les personnes âgées.
- ↑ 9,0 9,1 9,2 9,3 et 9,4 Johann Benedict Listing (1808 - 1882) mathématicien et physiologiste allemand à qui on doit la découverte de quelques propriétés topologiques de surface dont celle du ruban de Möbius qu'il découvrit indépendamment de ce dernier, ainsi que la loi de Listing de physiologie de l'œil, gouvernant les orientations de ce dernier dans son orbite lors de saccades oculaires.
Modèle:AlAugust Ferdinand Möbius (1790 - 1868) mathématicien et astronome théoricien allemand essentiellement connu pour sa découverte du ruban de Möbius, surface non orientable à deux dimensions avec seulement une face quand elle est plongée dans un espace euclidien à trois dimensions, cette surface fut découverte indépendamment par Listing. - ↑ 10,00 10,01 10,02 10,03 10,04 10,05 10,06 10,07 10,08 10,09 10,10 10,11 10,12 10,13 10,14 10,15 10,16 10,17 10,18 et 10,19 Dans le programme de physique de P.C.S.I., il est dit « lentille » mais en fait il ne s'agit pas de lentille mais de « dioptre sphérique », la différence du point de vue « conjugaison » est minime, il faut tenir compte de l'indice de l'espace image qui est différent de celui de l'espace objet alors qu'ils sont usuellement identiques dans une lentille la relation de conjugaison approchée de position de Descartes d'un dioptre sphérique avec origine au sommet étant Modèle:Nobr avec vergence du dioptre sphérique où et sont les distances focales image et objet de ce dioptre sphérique », la relation de conjugaison approchée de grandissement transverse de Descartes du même dioptre sphérique avec origine au sommet étant Modèle:Nobr » voir la solution des questions « conclusion : stigmatisme approché du dioptre sphérique (concave convergent) pour le point objet Ao et relation de conjugaison (approchée) de position de Descartes (avec origine au sommet) » et « relation de conjugaison (approchée) de grandissement transverse de Descartes (avec origine au sommet) » de l'exercice « stigmatisme et aplanétisme approchés d'un dioptre sphérique sous conditions de Gauss » de la série de la leçon « Signaux physiques (PCSI) » soit, sachant que l'espace objet est usuellement l'air, « avec » et Modèle:Nobr » semblable aux relations d'une lentille à condition de remplacer l'abscisse de Descartes de l'image par le dioptre par l'abscisse de Descartes d'une image corrigée utilisée par la lentille se substituant au dioptre ;
Modèle:Alles « dioptres sphériques » n'étant pas au programme de physique de P.C.S.I. et les relations de conjugaison étant semblables nous employons le terme « pseudo lentille ». - ↑ En fait la « pseudo lentille » modélise les dioptres sphériques successifs et le cristallin, mais pour plus de commodité nous appellerons « cristallin » la « pseudo lentille » de modélisation.
- ↑ Et donc voir nets des objets situés à courte distance de l'œil.
- ↑ 13,00 13,01 13,02 13,03 13,04 13,05 13,06 13,07 13,08 13,09 13,10 et 13,11 La dioptrie de symbole est l'unité de mesure de la vergence «».
- ↑ 14,0 14,1 14,2 et 14,3 On rappelle que de cette « pseudo lentille » modélisant un dioptre sphérique entre l'air et un milieu d'indice représentant une moyenne des indices du cristallin et des différentes humeurs utilise des images corrigées d'abscisse de Descartes ; ainsi la vergence de la pseudo lentille est avec la distance focale image de la pseudo lentille conduisant à une distance focale image du dioptre sphérique équivalent égale à positionnant le foyer principal image du dioptre sphérique équivalent à la distance du sommet alors que le foyer principal image de la pseudo lentille serait positionné à la distance de son centre optique .
- ↑ Et donc voir nets des objets situés à grande distance de l'œil.
- ↑ La signification de « normal » ici est « moyen » c.-à-d. le plus couramment rencontré.
- ↑ 17,0 et 17,1 C.-à-d. normal au sens de le plus couramment rencontré.
- ↑ 18,0 et 18,1 Plus précisément cette distance représente l'écart séparant « le sommet du dioptre sphérique équivalent ou du centre optique de la pseudo lentille situé sur l'axe optique principal au-delà du sommet de la cornée » et « le point de la rétine sur l'axe optique principal », c.-à-d. très grossièrement la profondeur moyenne d'un œil « emmétrope » quelle que soit l'accommodation de ce dernier.
- ↑ En effet lorsque le cristallin s'amincit au maximum la vergence de la pseudo lentille est et sa distance focale image correspondant à une distance focale image du dioptre sphérique équivalent c.-à-d. que le foyer principal image de ce dioptre est situé à au-delà du sommet du dioptre.
- ↑ 20,0 et 20,1 On rappelle que, travaillant dans les conditions d'aplanétisme de Gauss, la rétine est limitée à la partie transversale plane relativement à l'axe optique principal.
- ↑ Le PR d'un œil emmétrope est donc situé à l'infini de l'œil.
- ↑ 22,0 et 22,1 Voir le paragraphe « définition d'un objet linéique transverse » du chap. de la leçon « Signaux physiques (PCSI) ».
- ↑ Usuellement notée en absence d'ambiguïté.
- ↑ 24,0 et 24,1 Cette distance varie d’un individu à un autre et change avec l’âge.
- ↑ La relation de conjugaison de Descartes de la pseudo lentille s'écrit avec l'abscisse de Descartes de l'image corrigée utilisée par la Modèle:Nobr relation identique à la relation de conjugaison de Descartes du dioptre sphérique équivalent avec l'abscisse de Descartes de l'image donnée par le dioptre ;
Modèle:Alde la valeur de la vergence ainsi que du positionnement de la rétine, plan conjugué du plan contenant l'objet quand ce dernier est au plus proche de l'œil, on en déduit la valeur de la distance minimale de vision distincte par «» car ou, avec , «» soit ou et enfin « » ou «». - ↑ On peut donc affirmer l'assertion suivante “quand l'œil passe de l'absence d'accommodation à l'accommodation maximale, le foyer image se rapproche de du cristallin”.
- ↑ L'utilisation de la pseudo lentille introduisant un espace image corrigé pour tenir compte de l'indice de ce dernier avec une image corrigée liée à l'image effective par , soit une application du facteur multiplicateur pour positionner les images corrigées à partir des images effectives le long de l'axe optique principal ; dans ce modèle la rétine corrigée serait à du centre optique de la pseudo lentille.
- ↑ Le foyer principal image corrigé de la pseudo lentille est centré sur la rétine corrigée c.-à-d. à au-delà du centre optique de la pseudo lentille.
- ↑ 29,0 et 29,1 On rappelle que la relation de conjugaison de Descartes de la pseudo lentille, avec l'introduction des images corrigées selon , est .
- ↑ Ceci ayant pour conséquence que le foyer principal objet de la pseudo lentille est symétrique, relativement au centre optique de cette dernière, du foyer principal image corrigé de la pseudo lentille.
- ↑ Le foyer principal image corrigé de la pseudo lentille est situé en deçà de la rétine corrigée c.-à-d. à au-delà du centre optique de la pseudo lentille.
- ↑ Ceci ayant pour conséquence que le foyer principal objet de la pseudo lentille est symétrique, relativement au centre optique de cette dernière, du foyer principal image corrigé de la pseudo lentille.
- ↑ Qualificatif « moyen » car ce critère suppose que les images ponctuelles sont centrées sur les cellules qu'elles impressionnent ; dans le cas où ce ne serait pas le cas, le critère peut être trop ou pas assez restrictif.
- ↑ Willebrord Snell Van Royen ou Snellius (1580 - 1626) humaniste, mathématicien et physicien néerlandais, semble avoir découvert les lois portant son nom avant Descartes sans que ce soit Modèle:Nobr
Modèle:AlRené Descartes (1596 - 1650) mathématicien, physicien et philosophe français, considéré comme l'un des fondateurs de la philosophie moderne, en physique a contribué à l'optique géométrique et en mathématiques est à l'origine de la géométrie analytique. - ↑ Voir le paragraphe « 2ème loi de Snell - Descartes de la réfraction » du chap. de la leçon « Signaux physiques (PCSI) ».
- ↑ Ou 2ème loi de Kepler de la réfraction, on rappelle que les angles étant petits, la 2ème relation de Snell - Descartes de la réfraction se réécrit en omettant les sinus relation approchée de Kepler.
Modèle:AlJohannes Kepler (1571 - 1630) ou Johannes Keppler astronome allemand, surtout connu pour avoir étudié l'hypothèse héliocentrique de Nicolas Copernic (1473 - 1543) chanoine, médecin et astronome polonais et avoir découvert que les planètes suivent une trajectoire elliptique autour du Soleil c'est lors de l'étude de l'orbite de Mars qu'il voit la nécessité de se pencher sur l'optique à cause de la réfraction atmosphérique. - ↑ étant le diamètre d'une cellule de la rétine.
- ↑ Ou la valeur minimale de , angle séparant deux axes optiques secondaires.
- ↑ En France les opticiens utilisent préférentiellement l'acuité visuelle de l'œil exprimée en « dixièmes d'acuité », le lien entre et la limite de résolution angulaire en étant Modèle:Nobr » ainsi « c.-à-d. dixièmes d'acuité » correspond à une « limite de résolution angulaire » et une « acuité visuelle de dixièmes ou » correspond à une « limite de résolution angulaire » ;
Modèle:Alon rappelle qu'il y a « dans ». - ↑ « Une minute d'angle étant à ».
- ↑ 41,0 et 41,1 Ou, en ordre de grandeur, «».
- ↑ Il s'agit d'une valeur moyenne, on rencontre assez souvent la valeur simplifiée de comme limite de résolution angulaire de l'œil.
- ↑ C.-à-d. l'angle entre les droites qui relient les extrémités de l'objet et l'observateur, encore appelé taille apparente.
- ↑ La limite de résolution angulaire de l'œil dans cette formule doit être en .
- ↑ Valeur de en voir le paragraphe « notion de limite de résolution angulaire de l'œil » plus haut dans ce chapitre.
- ↑ En effet, en utilisant soit , on obtient une distance minimale de que l'on peut arrondir à .
- ↑ Cette distance correspond aussi à « deux points positionnés à de l'œil séparés de » ou à « deux points séparés de et positionnés à de l'œil ».
Modèle:AlConventionnellement, un œil a une acuité visuelle de dixièmes, s'il fait la résolution de deux points séparés de et positionnés à ce qui présuppose une limite de résolution angulaire de . - ↑ Ce sont les deux principales causes de myopie, la plus fréquente étant que l'œil est trop long la distance séparant la « pseudo lentille » modélisant l'association « dioptres sphériques - cristallin » et la rétine étant supérieure à ,
Modèle:AlModèle:Transparentla 2ème cause correspondant à une « pseudo lentille » trop convergente pouvant résulter d'un excès de courbure de la cornée ou du cristallin ;
Modèle:Alparmi les autres causes de myopie citons un « indice de cristallin trop grand » induisant une de l'indice de l'espace image de la « pseudo lentille » et par suite une de la vergence la vergence d'un dioptre sphérique et par conséquent de la pseudo lentille modélisant le dioptre sphérique équivalent valant voir la solution de la question « conclusion : stigmatisme approché d'un dioptre sphérique (concave convergent) pour le point objet Ao et relation de conjugaison (approchée) de position de Descartes (avec origine au sommet) » de l'exercice « Stigmatisme et aplanétisme approchés d'un dioptre sphérique sous conditions de Gauss » de la série de la leçon « Signaux physiques (PCSI) », ce type de myopie étant qualifiée « d'indice ». - ↑ Cela est évident si l'œil est trop profond, la vergence de la « pseudo lentille » restant égale à celle d'un œil emmétrope c.-à-d. normal ; si la myopie correspond à un excès de courbure ou dans le cas d'une myopie d'indice, la vergence de la « pseudo lentille » plus exactement la vergence sans accommodation devenant à et celle avec accommodation maximale aussi devenant à et la distance focale image se réécrivant avec l'expression de la vergence du dioptre sphérique équivalent selon , car à indice constant dans le cas d'un excès de courbure ou car à courbure constante dans le cas d'une myopie d'indice.
- ↑ En effet si nous supposons que la myopie est due à une trop grande convergence de l'œil n'accommodant pas, par exemple à au lieu de et l'application de la relation de conjugaison approchée de position de Descartes positionne le PR comme conjugué par la pseudo lentille du point de la rétine soit ou dont on déduit soit numériquement plaçant le PR en deçà de l'œil myope ;
Modèle:AlModèle:Transparentsi nous supposons que la myopie est due à une trop grande profondeur de l'œil n'accommodant pas, par exemple , la vergence de l'œil myope n'accommodant pas étant , l'application de la relation de conjugaison approchée de position de Descartes positionne le PR comme conjugué par la pseudo lentille du point de la rétine soit et numériquement plaçant le PR en deçà de l'œil myope. - ↑ En effet si nous supposons que la myopie est due à une trop grande convergence de l'œil accommodant au maximum, par exemple dont nous déduisons au lieu de pour un œil normal et l'application de la relation de conjugaison approchée de position de Descartes positionne le PP comme conjugué par la pseudo lentille du point de la rétine soit ou dont on déduit plaçant le PP en deçà de l'œil myope au lieu de ;
Modèle:AlModèle:Transparentsi nous supposons que la myopie est due à trop grande profondeur de l'œil n'accommodant pas, par exemple , la vergence de l'œil myope accommodant au maximum étant , l'application de la relation de conjugaison approchée de position de Descartes positionne le PP comme conjugué par la pseudo lentille du point de la rétine soit et numériquement plaçant le PP en deçà de l'œil myope au lieu de . - ↑ Cela est évident si l'œil est trop court, la vergence de la « pseudo lentille » restant égale à celle d'un œil emmétrope c.-à-d. normal ; si l'hypermétropie correspond à un défaut de courbure, la vergence de la « pseudo lentille » plus exactement la vergence sans accommodation devenant à et celle avec accommodation maximale aussi devenant à et la distance focale image se réécrivant avec l'expression de la vergence du dioptre sphérique équivalent selon , car à indice constant dans le cas d'un défaut de courbure.
- ↑ En effet si nous supposons que l'hypermétropie est due à une trop faible convergence de l'œil n'accommodant pas, par exemple à au lieu de et l'application de la relation de conjugaison approchée de position de Descartes positionne le PR comme conjugué par la pseudo lentille du point de la rétine soit ou dont on déduit soit numériquement plaçant le PR virtuel au delà de l'œil hypermétrope ;
Modèle:AlModèle:Transparentsi nous supposons que l'hypermétropie est due à une trop courte profondeur de l'œil n'accommodant pas, par exemple , la vergence de l'œil hypermétrope n'accommodant pas étant , l'application de la relation de conjugaison approchée de position de Descartes positionne le PR comme conjugué par la pseudo lentille du point de la rétine soit et numériquement plaçant le PR virtuel au delà de l'œil hypermétrope. - ↑ En effet si nous supposons que l'hypermétropie est due à trop faible convergence de l'œil accommodant au maximum, par exemple dont nous déduisons au lieu de pour un œil normal et l'application de la relation de conjugaison approchée de position de Descartes positionne le PP comme conjugué par la pseudo lentille du point de la rétine soit ou dont on déduit plaçant le PP en deçà de l'œil hypermétrope au lieu de ;
Modèle:AlModèle:Transparentsi nous supposons que l'hypermétropie est due à trop faible profondeur de l'œil n'accommodant pas, par exemple , la vergence de l'œil hypermétrope accommodant au maximum étant , l'application de la relation de conjugaison approchée de position de Descartes positionne le PP comme conjugué par la pseudo lentille du point de la rétine soit et numériquement plaçant le PP en deçà de l'œil hypermétrope au lieu de . - ↑ Dans le cas où la vergence de l'œil myope n'accommodant pas serait «», la vergence de la lentille divergente à accoler serait « » pour que le PR de l'œil myope corrigé soit à l'infini.
- ↑ Dans le cas où « la profondeur de l'œil myope serait », la vergence de la lentille divergente à accoler serait égale à « Modèle:Nobr
- ↑ Ce qui est le cas dans l'exemple que nous avons considéré jusqu'à présent avec et mais ce n'est pas toujours le cas ;
Modèle:Alpar exemple, dans le cas suivant , il faudrait remplacer la lentille divergente de pour la vision de loin par une lentille divergente de pour la vision de près. - ↑ Dans le cas où la profondeur de l'œil myope serait , la vergence de la lentille divergente à accoler serait égale à il s'agit donc de la même lentille divergente que celle nécessaire pour éloigner à l'infini le PR de l'œil myope.
- ↑ Dans le cas où la vergence de l'œil hypermétrope n'accommodant pas serait «», la vergence de la lentille convergente à accoler serait « » pour que le PR de l'œil hypermétrope corrigé soit à l'infini.
- ↑ Dans le cas où « la profondeur de l'œil hypermétrope serait », la vergence de la lentille convergente à accoler serait égale à « Modèle:Nobr
- ↑ Ce qui est le cas dans l'exemple que nous avons considéré jusqu'à présent avec et mais ce n'est pas toujours le cas ;
Modèle:Alpar exemple, dans le cas suivant , il faudrait remplacer la lentille convergente de pour la vision de loin par une lentille convergente de pour la vision de près. - ↑ Dans le cas où la profondeur de l'œil hypermétrope serait , la vergence de la lentille convergente à accoler serait il s'agit donc de la même lentille convergente que celle nécessaire pour fixer à l'infini le PR de l'œil hypermétrope.
- ↑ Suivant les plans d'incidence utilisés l'œil astigmate n'accommodant pas n'a pas les mêmes positions des foyers principaux image, le punctum remotum et aussi le punctum proximum obtenu avec l'œil astigmate accommodant au maximum a une position dépendant du plan d'incidence utilisé ;
Modèle:Alpar exemple si le punctum proximum est de pour une direction d'objet transverse verticale, il peut être de pour la direction transverse horizontale ces valeurs ne sont que des exemples,
Modèle:Alun objet plan situé à de l'œil astigmate accommodant au maximum verra net verticalement et flou horizontalement alors que
Modèle:Alsi cet œil accommode un peu moins pour faire la mise au point sur la direction horizontale, la direction verticale apparaîtra floue. - ↑ Un excimère est un dimère qui n'est stable qu'à l'état excité et se dissocie à l'état fondamental, par exemple le diargon ou le dikrypton ou encore le dixenon sont des excimères obtenus par stimulation électrique des gaz rares correspondant, ces excimères stables quand ils sont excités se désexcite en leur monomère en émettant un rayonnement laser ultraviolet par exemple laser à émettant un rayonnement de .
- ↑ Un exciplexe est un complexe qui n'est stable qu'à l'état excité et se dissocie à l'état fondamental, par exemple le fluorure de Krypton le plus couramment utilisé ou le fluorure d'Argon laser autorisé en chirurgie ophtalmologique, ces exciplexes stables quand ils sont excités se désexcite en leurs composants en émettant un rayonnement laser ultraviolet par exemple laser à émettant un rayonnement de et laser à un rayonnement de .
- ↑ C.-à-d. une ablation de matière par photon ; l'action des photons émis par « laser à exciplexe » le plus couramment utilisé sur la cornée est d'enlever de fines couches de matière par rupture de liaison et non de brûler les cellules visées ;
Modèle:Alle domaine d'utilisation des « lasers à exciplexe » ou des « lasers à excimère » ne se limite pas à la chirurgie ophtalmologique, mais ils ont également un grand intérêt dans les domaines de la micromécanique nécessitant une grande précision dans la définition des pièces utilisées et de l'industrie des semi-conducteurs.



![Coupe du modèle de Listing[9] d'un œil emmétrope avec position (en rouge) de son foyer principal image sans accommodation associée à son PR et position (en bleu) de son foyer principal image avec accommodation maximale associée à son PP](https://upload.wikimedia.org/wikipedia/commons/f/ff/%C5%92il_de_Listing.jpg)
![Coupe du modèle de Listing[9] d'un œil emmétrope avec axe optique secondaire, position (en rouge) de son foyer secondaire image sans accommodation associée à son PR, position (en bleu) de son foyer secondaire image avec accommodation maximale associée à son PP](https://upload.wikimedia.org/wikipedia/commons/0/0d/%C5%92il_de_Listing_-_axe_optique_secondaire.jpg)