Signaux physiques (PCSI)/Optique géométrique : réflexion, réfraction, lois de Descartes
Notion de miroirs et de dioptres
Miroir
Modèle:Définition
Modèle:AlExemples : miroir « plan », miroir « sphérique concave », miroir « sphérique convexe », miroir « parabolique » concave ou convexe
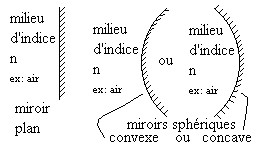
Modèle:AlModèle:TransparentVoir schémas ci-dessous à gauche à l'exception des miroirs paraboliques :
-
Schémas de miroirs plan Modèle:Alet Modèle:Alsphériques convexe et concave
-
Dioptre
Modèle:Définition
Modèle:AlExemples : dioptre « plan », dioptre « sphérique »
Modèle:AlModèle:TransparentVoir schémas ci-dessus à droite :
Réflexion métallique

Modèle:AlConsidérons un rayon lumineux arrivant sur une surface métallique en , point d'incidence, et faisant un angle d'incidence non orienté avec la normale en à la surface métallique ; la puissance lumineuse transportée par ce rayon subit, en grande partie, à l'arrivée sur la surface métallique, une « réflexion » c.-à-d. que la puissance lumineuse est renvoyée dans le milieu d’où elle vient, qualifiée de « métallique » ;
Modèle:Alil existe néanmoins une faible partie qui se propage dans le métal en s’atténuant très fortement on dit qu’il y a « absorption » pour cette partie, ceci entraînant un léger échauffement du métal et on définit un « facteur de réflexion énergétique » donnant le « pourcentage de puissance lumineuse réfléchie relativement à la puissance lumineuse reçue » :
- en incidence normale angle d'incidence non algébrisé , pour « l’un des meilleurs conducteurs métalliques l'»[1] ;
- le facteur de réflexion énergétique dépend de l'angle d'incidence et aussi de l'état de polarisation de la lumière[2] voir graphe ci-contre ;
- le facteur de réflexion énergétique dépend aussi de la longueur d’onde dans le vide : pour « l’un des meilleurs conducteurs métalliques l'» la réflexion est « relativement sélective »[3], seulement pour l’U.V. proche au lieu de pour le jaune du visible.
Modèle:AlLa réflexion métallique est dite « parfaite »[4] si le facteur de réflexion énergétique quelle que soit la longueur d’onde dans le vide et l’angle d’incidence non algébrisé .
Réflexion et réfraction dioptriques

Modèle:AlConsidérons toujours un rayon lumineux arrivant sur une surface dioptrique en , point d'incidence, et faisant un angle d'incidence non orienté avec la normale en à la surface dioptrique ; la puissance lumineuse peut se propager partiellement dans le milieu situé au-delà du dioptre ceci définissant une « réfraction » en changeant de direction[5], le reste subissant une réflexion « partielle »[6] et qualifiée de « dioptrique » ;

Modèle:Alon définit également un « facteur de réflexion énergétique » donnant le « pourcentage de puissance lumineuse réfléchie relativement à la puissance lumineuse reçue »[7] :
- En incidence normale, le facteur de réflexion énergétique est « très faible »[8] : seulement pour le « dioptre air - verre », pour le « dioptre air - eau », pour le « dioptre eau - verre »
- Le facteur de réflexion énergétique varie fortement avec l’angle d’incidence non algébrisé , atteignant en « incidence rasante » c.-à-d. quand l'angle d'incidence non algébrisé tend vers : pour le « dioptre air - verre » le « facteur de réflexion énergétique moyen »[9] vaut , , voir « figures »[10] ci-contre à gauche pour l'onde polarisée perpendiculairement et à droite pour l'onde polarisée parallèlement.
Les deux lois de Snell-Descartes de la réflexion
Modèle:AlLes lois de Snell - Descartes[11] de la réflexion sont des postulats de l'optique géométrique, elles sont validées par vérification expérimentale[12].
Quelques définitions relatives à la réflexion métallique ou dioptrique
Modèle:AlOn donnera ces définitions relativement à un miroir sur lequel il y a réflexion métallique, mais elles restent valables pour la réflexion sur un dioptre.

Modèle:AlSoit un rayon incident quelconque avec appelé « point d'incidence », on lui associe la normale au miroir en orientée dans le sens incident par et dans le sens réfléchi par [13] ;
Modèle:Alsoit le vecteur unitaire orientant le rayon incident[14], on définit dans le cas où le rayon incident n'est pas normal c.-à-d. au miroir en le plan comme « plan d'incidence associé au rayon incident »[15], le plan d'incidence étant orienté de façon arbitraire[16] ;
Modèle:All'angle orienté est appelé « angle d'incidence associé au rayon incident »[17], il peut prendre toute valeur de en [18] les bornes de cet intervalle ne sont pas des valeurs permettant une réflexion mais, un angle d'incidence tendant vers la borne inférieure par valeur supérieure ou vers la borne supérieure par valeur inférieure conduit à une réflexion, le rayon incident étant dit « rasant ».
Modèle:AlSoit le rayon « réfléchi » correspondant au rayon incident précédemment défini[19], on l’oriente par le vecteur unitaire dans le sens de propagation du rayon réfléchi, et on définit dans le cas où le rayon réfléchi n'est pas normal c.-à-d. au miroir en le plan comme « plan de réflexion associé au rayon réfléchi »[20], le plan de réflexion étant « orienté en liaison avec celle du plan d’incidence »[21] ;
Modèle:All'angle orienté est appelé « angle de réflexion associé au rayon réféchi », il peut prendre toute valeur de en [18] là encore les bornes de cet intervalle ne sont pas des valeurs correspondant à une réflexion mais, un angle de réflexion tendant vers la borne inférieure par valeur supérieure ou vers la borne supérieure par valeur inférieure correspond à une réflexion effective, le rayon réfléchi étant dit « rasant ».
Première loi de Snell-Descartes de la réflexion
Deuxième loi de Snell-Descartes de la réflexion
Les deux lois de Snell-Descartes de la réfraction
Modèle:AlLa « réfraction dioptrique » est la poursuite de la propagation au-delà du dioptre avec un éventuel changement de direction[22].
Modèle:AlLes lois de Snell - Descartes[11] de la réfraction[23] sont également des postulats de l'optique géométrique, elles sont validées par vérification expérimentale[12].
Quelques définitions relatives à la réfraction dioptrique

Modèle:AlSoit un rayon incident quelconque avec appelé « point d'incidence », on lui associe la normale au dioptre en orientée le vecteur unitaire [24] ;
Modèle:Alsoit le vecteur unitaire orientant le rayon incident[14], on définit dans le cas où le rayon incident n'est pas normal c.-à-d. au miroir en le plan comme « plan d'incidence associé au rayon incident »[15], le plan d'incidence étant orienté de façon arbitraire[16] ;
Modèle:All'angle orienté est appelé « angle d'incidence associé au rayon incident »[17], il peut prendre toute valeur de en [18] les bornes de cet intervalle ne sont pas des valeurs permettant une réfraction mais, un angle d'incidence tendant vers la borne inférieure par valeur supérieure ou vers la borne supérieure par valeur inférieure peut conduire à une réfraction[25], le rayon incident étant dit « rasant ».
Modèle:AlSoit le rayon « réfracté » correspondant au rayon incident précédemment défini[26], on l’oriente par le vecteur unitaire dans le sens de propagation du rayon réfracté, et on définit dans le cas où le rayon réfracté n'est pas normal c.-à-d. au dioptre en le plan comme « plan de réfraction associé au rayon réfracté »[27], le plan de réfraction étant « orienté en liaison avec l'orientation du plan d’incidence »[28] ;
Modèle:All'angle orienté est appelé « angle de réfraction associé au rayon réfracté », il peut prendre une valeur de en [18] les bornes de cet intervalle ne sont pas des valeurs correspondant à une réfraction mais, un angle de réfraction tendant vers la borne inférieure par valeur supérieure ou vers la borne supérieure par valeur inférieure peut sous réserve de positionnement de l'indice du milieu émergent relativement à celui du milieu incident [29] correspondre à une réfraction effective, le rayon réfracté étant dit « rasant ».
Première loi de Snell-Descartes de la réfraction
Deuxième loi de Snell-Descartes de la réfraction
Modèle:Théorème Modèle:AlCommentaires : permet de comparer à suivant le rapport :
- tout d'abord montrant qu'« un rayon incident normal traverse le dioptre sans déviation »,
- ensuite, et sont de même signe, montrant qu'« un incident et son réfracté au point d'incidence sont toujours situés de part et d'autre de la normale en à la surface dioptrique »,
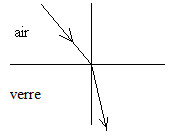
- enfin, « si exemple dioptre air - verre» , nous en déduisons «»[30] soit, sachant que , «» Modèle:Nobr c.-à-d. « un rayon passant d'un milieu moins réfringent à un milieu plus réfringent se réfracte en se rapprochant de la normale » voir ci-dessous à gauche,
-
Disposition du rayon réfracté relativement au rayon incident dans une réfraction air - verre
-
Disposition du rayon réfracté relativement au rayon incident dans une réfraction verre - air
- alors que « si exemple dioptre verre - air» , nous en déduisons «»[31] soit, dans la mesure où il y a réfraction et sachant que , «» [32] c.-à-d. « un rayon passant d'un milieu plus réfringent à un milieu moins réfringent se réfracte en s'éloignant de la normale »[33] voir ci-dessus à droite.
Cône limite de réfraction dans le cas du passage d'un milieu moins réfringent à un milieu plus réfringent
Modèle:AlLe rayon réfracté étant plus proche de la normale que le rayon incident, la variation de
de
à
entraîne une « variation moindre de
de
à
» où «
est l’angle limite de réfraction » défini par

Modèle:Alà un rayon incident quelconque arrivant en un point d’incidence fixé, correspondra un rayon réfracté issu de et se trouvant à l’intérieur d’un cône de révolution[34], de sommet , d’axe normal au dioptre en et de demi-angle au sommet ; ce cône est appelé « cône limite de réfraction enModèle:Nobr voir figure ci-contre plaçant un diaphragme sur le dioptre, ne permettant de faire passer la lumière qu’à travers , et supposant que la seule source de lumière se trouve du côté de l’air, seul le cône de réfraction en sera éclairé, le reste étant dans l’obscurité et par suite, un poisson situé hors de ce cône ne pourra pas être vu par le pêcheur situé dans le milieu « air » car aucun rayon incident arrivant en ne pourra atteindre le poisson.
Modèle:AlPassage air - eau : «»,
Modèle:Alpassage air - verre : «»[35] et
Modèle:Alpassage eau - verre : «»[35].
Cône limite d'incidence pour qu'il y ait réfraction dans le cas d'un milieu plus réfringent à un milieu moins réfringent
Modèle:AlLe rayon réfracté étant plus éloigné de la normale que le rayon incident, la variation de de à correspond à une « variation moindre de de à » où « est l’angle limite d'incidence pour qu'il y ait réfraction » défini par


Modèle:Alà un rayon réfracté quelconque issu d'un point d’incidence , correspond un rayon incident passant par et se trouvant à l’intérieur d’un cône de révolution[34], de sommet , d’axe normal au dioptre en et de demi-angle au sommet ; ce cône est appelé « cône limite d'incidence pour qu'il y ait réfraction en»[36], voir figure ci-contre à gauche plaçant un diaphragme sur le dioptre, ne permettant de faire passer la lumière qu’à travers , et supposant que la seule source de lumière se trouve du côté du Modèle:Nobr on peut restreindre le cône incident de lumière en à son cône limite d'incidence pour qu'il y ait réfraction sans qu'il y ait une quelconque modification sur la puissance lumineuse reçue du côté de l'air ;
Modèle:Alsur la figure ci-contre à droite, représentation d'un rayon incident situé hors du cône limite d'incidence pour qu'il y ait réfraction en , ce rayon subissant une réflexion totale il ne faut pas perdre de vue que « la réfraction n'est toujours que partielle, le reste subissant une réflexion »[37] par conséquent, si la réfraction n'est pas possible, « la réflexion devient totale » ; « si »[38] ou, si un rayon incident passant par est situé « hors du cône limite d'incidence pour qu'il y ait réfraction en », il y a « réflexion totale » voir figure ci-dessus à droite.
Modèle:AlRemarque : L'angle limite de réfraction pour le dioptre « air - eau » étant défini par et l'angle limite d'incidence pour qu'il y ait réfraction sur le dioptre « eau - air » par , nous constatons qu'il s'agit de la même relation de définition d'où «» valable quel que soit le dioptre.
Angle limite d'un dioptre
Modèle:AlPour tout dioptre séparant deux milieux d'indices différents, l'un des deux est nécessairement le plus petit, nous définissons alors
- l'angle limite de réfraction si la lumière passe du milieu le moins réfringent au milieu le plus réfringent,
- l'angle limite d'incidence pour qu'il y ait réfraction si la lumière passe du milieu le plus réfringent au milieu le moins réfringent.
Retour sur la propagation dans un milieu inhomogène
Modèle:AlNous avons indiqué dans la note « 38 » du chap. de la leçon « Signaux physiques (PCSI) » que « la propagation cesse d'être rectiligne dans un milieu inhomogène » voir le paragraphe « milieu inhomogène » du chap. de la leçon « Signaux physiques (PCSI) » en précisant la forme de la propagation dans une solution saturée saline d'une part et d'autre part celle dans l'air des régions « chaude ou froide » [39] créant l'apparition de mirages rappel ci-dessous ;
-
Propagation incurvée d'un faisceau cylindrique laser dans une solution saline saturée
-
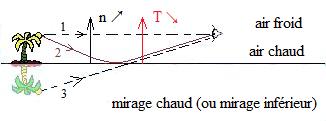
Mirage chaud ou inférieur dû à un gradient de température d'air vertical descendant
-
Mirage froid ou supérieur dû à un gradient de température d'air vertical ascendant
Modèle:Alnous expliquons ces phénomènes simplement en remplaçant le milieu inhomogène dans lequel l'indice varie continûment avec l'altitude par une juxtaposition verticale de couches planes de faible épaisseur de milieux homogènes d'indices différents d'une couche à l'autre ainsi :
- dans une solution saline saturée non homogénéisée telle que la concentration quand et, comme est une fonction de , quand nous pouvons considérer une succession verticale de couches de faible épaisseur de concentration constante donc d'indice constant, entraînant l'existence d'une succession de dioptres plans séparant deux milieux d'indices très voisins ; le milieu supérieur étant moins réfringent que le milieu inférieur, nous observons qu'un « rayon incident du milieu supérieur se réfracte vers le milieu inférieur en se rapprochant de la normale » d'où une courbure de la direction de propagation vers le bas voir figure ci-dessous à gauche ;
-
Explication de la propagation incurvée d'un faisceau cylindrique laser dans une solution saline saturée par réfraction à travers des couches horizontales de faible épaisseur
-
Explication d'un mirage chaud ou inférieur dû à un gradient de température d'air vertical descendant par réfraction à travers des couches horizontales de faible épaisseur
-
Explication d'un mirage froid ou supérieur dû à un gradient de température d'air vertical ascendant par réfraction à travers des couches horizontales de faible épaisseur
- dans une région chaude à forte variation de température par mètre d'altitude telle que la température quand et, comme est une fonction de , quand nous pouvons considérer une succession verticale de couches de faible épaisseur de température constante donc d'indice constant, entraînant l'existence d'une succession de dioptres plans séparant deux milieux d'indices très voisins ; le milieu supérieur étant plus réfringent que le milieu inférieur, nous observons tout d'abord qu'un « rayon incident du milieu supérieur se réfracte vers le milieu inférieur en s'éloignant de la normale » jusqu'à ce que l'incidence devienne rasante, la composante verticale de la propagation se faisant alors dans l'autre sens et on observe qu'« un rayon incident du milieu inférieur se réfracte vers le milieu supérieur en se rapprochant de la normale » d'où une courbure de la direction de propagation vers le haut voir figure ci-dessus au centre ;
- dans une région froide à forte variation de température par mètre d'altitude telle que la température quand et, comme est une fonction de , quand nous pouvons considérer une succession verticale de couches de faible épaisseur de température constante donc d'indice constant, entraînant l'existence d'une succession de dioptres plans séparant deux milieux d'indices très voisins ; le milieu inférieur étant plus réfringent que le milieu supérieur, nous observons tout d'abord qu'un « rayon incident du milieu inférieur se réfracte vers le milieu supérieur en s'éloignant de la normale » jusqu'à ce que l'incidence devienne rasante, la composante verticale de la propagation se faisant alors dans l'autre sens et on observe qu'« un rayon incident du milieu supérieur se réfracte vers le milieu inférieur en se rapprochant de la normale » d'où une courbure de la direction de propagation vers le bas voir figure ci-dessus à droite.
Interprétation des deuxièmes lois de Snell-Descartes à l'aide du modèle ondulatoire
Introduction
Modèle:AlNous avons considéré les lois de « Snell - Descartes »[11] comme postulats de l'optique géométrique mais il est possible d'avoir une autre approche en restant d'abord dans le cadre de l'optique ondulatoire pour déterminer quelques propriétés puis en se plaçant dans l'approximation de l'optique géométrique
ce qui revient à considérer
comme un infiniment petit relativement aux autres dimensions
;
Modèle:Alune « O.P.H. »[40] de longueur d'onde dans le vide
a une « phase instantanée égale à
» soit encore «
» en utilisant le « lien entre longueur d'onde
dans le milieu et celle
dans le vide
», soit enfin,
Modèle:AlModèle:Transparenten définissant le « chemin optique »
comme « la distance que la lumière parcourrait dans le vide pendant la même durée que celle qu'elle parcourt dans le milieu d'indice
» soit, pour une « distance géométrique
dans un milieu d'indice
», un chemin optique égal à «
», la réécriture de la phase instantanée selon
Interprétation de la deuxième loi de Snell-Descartes de la réfraction par utilisation du modèle ondulatoire

Modèle:AlUn « pinceau parallèle monochromatique » [41] arrivant sur le dioptre avec un angle d'incidence est associé, dans le modèle ondulatoire, à une « O.P.H. » [42] se propageant dans la direction faisant, avec la normale au dioptre, l'angle et
Modèle:Alcette « O.P.H. » émerge de la surface dioptrique en « O.P.H. » [43] se propageant dans une direction faisant, avec la normale au dioptre, un angle , cette « O.P.H. réfractée » étant associée à un « pinceau parallèle monochromatique » [44] d'angle de réfraction ;
Modèle:Aladmettant la 1ère loi de Snell - Descartes[11] de la réfraction, les directions des pinceaux incident et réfracté sont considérées dans un même plan normal passant par « le plan d'incidence » voir figure ci-contre,
Modèle:AlModèle:Transparentnous nous proposons de démontrer la 2ème loi de Snell - Descartes[11] de la réfraction à savoir « » ;
Modèle:Alles plans d'onde dont les traces sur le plan d'incidence sont respectivement
et
, étant des surfaces équiphases, nous en déduisons que le « chemin optique entre
et
» est le même que « celui entre
et
» soit «
» ou «
» ;
Modèle:Aldeux angles à côtés respectivement
étant égaux nous en déduisons «
» et «
» d'où «
» et «
» soit, par report dans
, «
» ou, par simplification par
,
Interprétation de la deuxième loi de Snell-Descartes de la réflexion par utilisation du modèle ondulatoire

Modèle:AlDans le cadre de l'optique ondulatoire et en admettant la 1ère loi de Snell - Descartes[11] de la réflexion nous pouvons procéder de même pour démontrer la 2ème loi de Snell - Descartes[11] de la réflexion ; pour cela nous considérons un « pinceau parallèle monochromatique » [41] arrivant sur la surface réfléchissante avec un angle d'incidence et nous lui associons une « O.P.H. »[42] se propageant dans la direction faisant, avec le vecteur unitaire normal à la surface réfléchissante orienté dans le sens incident, l'angle ;
Modèle:Alcette « O.P.H. » se réfléchit alors en « O.P.H. » [43] se propageant dans une direction faisant, avec le vecteur unitaire normale à la surface réfléchissante orienté dans le sens réfléchi, un angle , et à cette « onde plane réfléchie » on associe un « pinceau parallèle monochromatique » [44] d'angle de réflexion ;
Modèle:Aladmettant la 1ère loi de Snell - Descartes[11] de la réflexion, les directions des pinceaux incident et réfléchi sont considérées dans un même plan normal passant par « le plan d'incidence » voir figure ci-contre et nous nous proposons de démontrer la 2ème loi de Snell - Descartes[11] de la réflexion à savoir «» ;
Modèle:Alles plans d'onde dont les traces sur le plan d'incidence sont respectivement
et
, étant des surfaces équiphases, nous en déduisons que le « chemin optique entre
et
» est le même que « celui entre
et
» soit «
» ou «
»[45] ;
Modèle:Aldeux angles à côtés respectivement
étant égaux nous en déduisons «
» et «
» d'où «
» et «
» soit, par report dans
, «
» dont on déduit «
» et, compte-tenu du signe des angles visualisés sur la figure[46]
Conditions de réflexion totale dioptrique
Généralités
Modèle:AlNous avons vu, d'une part, qu'il y avait toujours réfraction quel que soit l'angle d'incidence si la lumière passait d'un milieu moins réfringent à un milieu plus réfringent car le rayon réfracté est plus proche de la normale que le rayon incident d'où une 1ère C.N.[47] pour qu'il n'y ait pas réfraction :
Modèle:Alla lumière doit passer d'un milieu plus réfringent à un milieu moins réfringent , exemple : dioptre « verre - air » ou « eau - air » ;
Modèle:Alnous avons vu, d'autre part, que dans ce cas, la condition de réfraction est que l'angle d'incidence soit strictement inférieur à l'angle limite du dioptre d'où une 2ème C.N.[47] pour qu'il y ait réflexion totale Modèle:Nobr à la 1ère C.N.[47], ces conditions s'avèrent suffisantes :
Modèle:All'angle d'incidence doit être supérieurau sens largeà l'angle limite du dioptre[48] ou «» «».
Applications
Modèle:AlLes applications de la réflexion totale sont nombreuses, citons en deux exemples :
Prisme à réflexion totale


Modèle:AlL'angle limite pour un dioptre « verre - air » avec un verre d'indice et l'air d'indice étant « », si un rayon se propageant dans le verre arrive sur une des surfaces dioptriques « verre - air » avec un angle d'incidence supérieur à , il sera totalement réfléchi comme sur les schémas ci-contre à gauche ou à droite :
Modèle:Al« équerre optique » sur le schéma de gauche un rayon incident normal entre par la face d'entrée sans être dévié, il rencontre le dioptre « verre - air » sous l'angle d'incidence [50] supérieur à l'angle limite d'où réflexion totale sur la face renvoyant le rayon perpendiculairement au rayon incident et enfin le rayon réfléchi arrivant normalement à la face de sortie n'est pas dévié,
Modèle:Alréalisation d'une « translation verticale » à l'aide de « deux équerres optiques » comme cela est nécessaire dans un périscope ou un appareil photographique « réflex » sur le schéma de droite. Modèle:Clr
Fibre optique guide de lumière

Modèle:AlUne fibre optique est constituée d'une âme cylindrique d'indice exemple entourée d'une gaine, enveloppe cylindrique, d'indice pour le même exemple ;
Modèle:Alune fibre est utilisée pour guider la lumière incidente pénétrant dans son âme par une extrémité et devant ressortir par l'autre extrémité sans avoir subi de réfraction sur la surface dioptrique « âme - gaine », il faut donc qu'un rayon qui atteindrait cette surface y arrive sous un angle d'incidence de valeur absolue supérieure à l'angle limite de ce dioptre «»[51] voir figure ci-contre où la fibre est courbée[52]. Modèle:Clr
Notes et références
- ↑ pour l' or, pour le cuivre et pour l'acier alliage métallique constitué de fer et d'une faible proportion de Modèle:Nobr à proportion de à en masse.
- ↑ Sur la figure on distingue le facteur de réflexion énergétique suivant l'état de polarisation de l'onde incidente, quand le champ électrique est perpendiculaire au plan d'incidence c.-à-d. le plan normal en , point d'incidence à la surface métallique et contenant le rayon incident et quand le champ électrique est dans le plan d'incidence.
- ↑ On peut rendre l’ moins sélectif du point de vue réflexion en déposant une couche mince de sulfure de zinc
- ↑ Seul cas étudié à ce niveau.
- ↑ Sauf dans le cas où .
- ↑ Dans certains cas pour certains milieux en présence et certains angles d’incidence non algébrisés, la réfraction peut ne pas se produire, il n’y a alors que réflexion et cette dernière est qualifiée de « totale ».
- ↑ Le complément à définissant le facteur de réfraction ou transmission énergétique c.-à-d. le pourcentage de puissance lumineuse transmise relativement à la puissance lumineuse reçue.
- ↑ On établit à considérer comme complément que et donc que le facteur énergétique de réflexion dioptrique sous incidence normale est d'autant plus petit que les indices sont proches
- ↑ On utilise un facteur de réflexion énergétique moyen car le coefficient de réflexion énergétique dépend aussi de l’état de polarisation de l’onde.
- ↑ Sur ces figures on distingue le facteur de réflexion énergétique suivant l'état de polarisation de l'onde incidente, quand le champ électrique est perpendiculaire au plan d'incidence et quand le champ électrique est dans le plan d'incidence ;
Modèle:Alon remarque que s'annule et par conséquent le facteur de transmission énergétique vaut 1 pour une valeur particulière d'angle d'incidence appelé « angle d'incidence de Brewster » ; si l'onde incidente n'est pas polarisée et si l'angle d'incidence a la valeur de Brewster, l'onde réfléchie est polarisée perpendiculairement au plan d'incidence puisque la composante n'est pas réfléchie ;
Modèle:AlDavid Brewster (1781 - 1868) physicien, inventeur et écrivain écossais, dans le domaine de la physique ses travaux portèrent sur la polarisation de la lumière par réflexion. - ↑ 11,00 11,01 11,02 11,03 11,04 11,05 11,06 11,07 11,08 11,09 et 11,10 Willebrord Snell Van Royen ou Snellius (1580 - 1626) humaniste, mathématicien et physicien néerlandais, semble avoir découvert les lois portant son nom avant Descartes sans que ce soit assuré.
Modèle:AlRené Descartes (1596 - 1650) mathématicien, physicien et philosophe français, considéré comme l'un des fondateurs de la philosophie moderne, en physique a contribué à l'optique géométrique et en mathématiques est à l'origine de la géométrie analytique. - ↑ 12,0 et 12,1 Il y a une autre approche remplaçant les deux lois de Snell - Descartes de la réflexion considérées comme postulats par un principe de l'optique géométrique « le principe de Fermat » « La lumière se propage d'un point à un autre sur des trajectoires telles que la durée du parcours soit localement minimale si on considère deux points voisins de la trajectoire, toute modification de cette dernière entre ces deux points figés correspondra à une augmentation de la durée de parcours» et les lois de Snell - Descartes de la réflexion en découlent par application du principe de Fermat ;
Modèle:AlPierre de Fermat (1ère décennie du XVIIème siècle - 1665) magistrat, polymathe qui a une connaissance approfondie d'un grand nombre de sujets différents dans le domaine des arts et des Modèle:Nobr et mathématicien français, surnommé « le prince des amateurs », habile latiniste et helléniste, s'étant intéressé, entre autres, à l'optique il a énoncé le principe « de Fermat » en mais n'a soumis son mémoire « Synthèse pour les réfractions » qu'en et à l'arithmétique il est surtout connu par le petit théorème de Fermat énoncé en mais sans démonstration « faute de place » et par le dernier théorème de Fermat encore appelé grand théorème de Fermat énoncé en tant que conjecture et démontré en par Andrew John Wiles (né en 1953) mathématicien britannique depuis ce théorème est judicieusement appelé « théorème de Fermat-Whiles ». - ↑ et étant des vecteurs unitaires.
- ↑ 14,0 et 14,1 Donc de direction « le rayon incident » et de sens « le sens de propagation » appelé « sens incident ».
- ↑ 15,0 et 15,1 Dans le cas où le rayon incident est normal, étant colinéaire à , tout plan au miroir en peut jouer le rôle de plan d'incidence associé au rayon incident normal non unicité de la notion de plan d'incidence dans ce cas.
- ↑ 16,0 et 16,1 Mais on choisit usuellement le sens «» de telle façon que l'angle d'incidence associé au rayon incident particulier considéré soit positif notion d'angle d'incidence définie ci-après.
- ↑ 17,0 et 17,1 L'angle étant orienté, son signe dépend du sens d'orientation arbitraire choisi dans le plan d'incidence mais, quand plusieurs rayons incidents sont définis dans un même plan d'incidence, on choisit usuellement le sens «» de façon que le plus grand nombre d'angles d'incidence soit positif ;
Modèle:Aldans le cas où le rayon incident est normal, l'angle d'incidence est nul et peu importe le choix du sens «». - ↑ 18,0 18,1 18,2 et 18,3 Ou de l'intervalle en .
- ↑ Sur la figure ci-dessus, il est représenté, en rouge, dans le plan d'incidence car nous verrons que la « première loi régissant la réflexion » le positionne dans le plan d'incidence mais, avant d'appliquer cette première loi, le rayon réfléchi pourrait être « dans n'importe quel plan contenant » d'où les définitions liées aux rayons réfléchi et incident indépendantes de cette première loi.
- ↑ Dans le cas où le rayon réfléchi est normal, étant colinéaire à , tout plan au miroir en peut jouer le rôle de plan de réflexion associé au rayon réfléchi normal non unicité de la notion de plan de réflexion dans ce cas.
- ↑ Si nous tenons compte de la « première loi régissant la réflexion » qui identifie le plan de réflexion et le plan d'incidence, l'orientation du plan de réflexion est identique à celle du plan d'incidence.
- ↑ En fait il y a toujours changement de direction sauf quand le rayon incident est normal c.-à-d. quand le rayon incident est à la surface dioptrique au point d'incidence .
- ↑ En ce qui concerne les lois de Snell - Descartes de la réfraction, il n'est pas assuré que Snell les ait pour la 1ère fois énoncées car il ne les a pas explicitement publiées mais la paternité lui en a été reconnue sous l'influence entre autres de Huygens qui, outré de la prétention des Français de revendiquer cette découverte pour le seul Descartes, mentionne dans ses publications, soixante-dix ans plus tard, les travaux de Snell dont il a eu connaissance Snell a développé des travaux lesquels aboutirent à la publication en de sa table des sinus permettant de positionner tout rayon réfracté connaissant le rayon incident.
Modèle:AlDescartes a publié en la loi de la réfraction dans son traité « Dioptrique », annexe du « Discours de la Méthode » Kepler avait déjà publié dans son « dioptrique » en , une loi de réfraction qui n'était applicable que pour les petits angles avant que Snell ne publie, en , sa table des sinus.
Modèle:AlChristian Huygens (1629 – 1695) ou Christian Huyghens mathématicien, astronome et physicien néerlandais est essentiellement connu pour sa théorie ondulatoire de la lumière.
Modèle:AlJohannes Kepler (1571 - 1630) ou Johannes Keppler astronome allemand, surtout connu pour avoir étudié l'hypothèse héliocentrique de Nicolas Copernic (1473 - 1543) chanoine, médecin et astronome polonais et avoir découvert que les planètes suivent une trajectoire elliptique autour du Soleil c'est lors de l'étude de l'orbite de Mars qu'il voit la nécessité de se pencher sur l'optique à cause de la réfraction atmosphérique.
Modèle:AlWillebrord Snell Van Royen ou Snellius (1580 - 1626) humaniste, mathématicien et physicien néerlandais et René Descartes (1596 - 1650) mathématicien, physicien et philosophe français : voir la note « 13 » plus haut dans ce chapitre pour plus de détails. - ↑ Sur la normale , les sens incident et émergent étant identiques, on ne définit qu'un seul vecteur unitaire orientant la normale pour l'incidence et la réfraction.
- ↑ Nous verrons qu'il peut ne pas y avoir réfraction pour une incidence rasante suivant la valeur de l'indice du milieu émergent relativement à celle du milieu incident plus précisément nous verrons que l'incidence rasante ne conduit pas à une réfraction si .
- ↑ Sur la figure ci-dessus, il est représenté, en rouge, dans le plan d'incidence car nous verrons que la « première loi régissant la réfraction » le positionne dans le plan d'incidence mais, avant d'appliquer cette première loi, le rayon réfracté pourrait être « dans n'importe quel plan contenant » d'où les définitions liées aux rayons réfracté et incident indépendantes de cette première loi.
- ↑ Dans le cas où le rayon réfracté est normal, étant colinéaire à , tout plan au dioptre en peut jouer le rôle de plan de réfraction associé au rayon réfracté normal non unicité de la notion de plan de réfraction dans ce cas.
- ↑ Si nous tenons compte de la « première loi régissant la réfraction » qui identifie le plan de réfraction et le plan d'incidence, l'orientation du plan de réfraction est identique à celle du plan d'incidence.
- ↑ Nous verrons plus précisément qu'il peut y avoir une émergence rasante pour une valeur d'angle d'incidence si .
- ↑ En multipliant de part et d'autre par .
- ↑ En multipliant de part et d'autre par .
- ↑ étant équivalent à et la fonction sinus étant .
- ↑ On pouvait aussi invoquer la loi de retour inverse de la lumière voir le paragraphe « 3ème loi : loi du retour inverse de la lumière » du chap. de la leçon « Signaux physiques (PCSI) » par rapport au cas précédent : le milieu d'indice le plus faible était le milieu d'entrée, il devient le milieu de sortie si on envisage un retour inverse simultanément les rayons incident et réfracté permutent, le rayon réfracté était plus proche de la normale que le rayon incident, le rayon incident devient plus proche de la normale que le rayon réfracté par application de la loi du retour inverse en fait il suffit de permuter les indices et .
- ↑ 34,0 et 34,1 Au lieu de considérer que le rayon réfracté ou incident passant par peut décrire un demi-plan situé d'un même côté du dioptre pour le rayon réfracté ou son opposé pour le rayon incident, correspondant à un angle de réfraction ou d'incidence pouvant être positif ou négatif, nous considérons que le rayon réfracté ou incident passant par décrit un quart de plan situé d'un même côté du dioptre pour le rayon réfracté ou son opposé par pour le rayon incident et correspondant à un angle de réfraction ou d'incidence positif, les valeurs négatives considérées précédemment s'obtenant maintenant avec les valeurs positives simultanément à une rotation du plan de réfraction ou d'incidence de autour de la normale en à la surface dioptrique.
- ↑ 35,0 et 35,1 Tous les verres ne sont pas d'indice .
- ↑ Pour justifier de ce cône nous pouvons aussi invoquer la loi de retour inverse de la lumière voir le paragraphe « 3ème loi : loi du retour inverse de la lumière » du chap. de la leçon « Signaux physiques (PCSI) » par rapport au cas précédent : le milieu d'indice le plus faible était le milieu d'entrée, il devient le milieu de sortie, le rayon réfracté permutant avec le rayon incident ; le rayon réfracté était plus proche de la normale que le rayon incident et était localisé dans le cône limite de réfraction de demi-angle au sommet égal à , par loi du retour inverse le rayon incident devient plus proche que le rayon réfracté et est localisé pour qu'il y ait réfraction dans le cône limite d'incidence de demi-angle au sommet égal à .
- ↑ Plus exactement une partie de la puissance incidente est réfractée, le reste étant réfléchi.
- ↑ Ici nous considérons de nouveau qu'un rayon incident passant par peut décrire tout le demi-plan situé d'un même côté du dioptre, l'angle d'incidence correspondant pouvant prendre une valeur positive ou négative.
- ↑ Ce n'est pas la température qui importe mais la variation de température ; pour qu'un mirage soit observable il faut qu'il y ait une variation de température d'au moins par mètre d'altitude soit au moins sur de dénivellation et plus la variation de température par mètre d'altitude est grande, mieux observable est le mirage.
- ↑ Onde Plane Harmonique ou onde plane progressive sinusoïdale donc nécessairement monochromatique.
- ↑ 41,0 et 41,1 C'est un pinceau monochromatique issu du point à l'infini dans la direction faisant l'angle d'incidence cité après.
- ↑ 42,0 et 42,1 Celle-ci ayant une expansion limitée dans l'espace, est soumise à une diffraction qui doit être inobservable pour que l'approximation de l'optique géométrique soit applicable c.-à-d. la longueur d'onde dans le vide de l'O.P.H. doit être très petite devant la dimension transversale du pinceau associé voir le paragraphe « approximation de l'optique géométrique » du chap. de la leçon « Signaux physiques (PCSI) ».
- ↑ 43,0 et 43,1 Pour la justification du fait que l'onde émergeant de la surface dioptrique ou réfléchissante est « plane » revoir le paragraphe « tentative d'explication de la diffraction à l'infini d'une O.P.H. par une fente infiniment longue » du chap. de la leçon « Signaux physiques (PCSI) », utilisant le « principe de Huygens - Fresnel contribution de Fraunhofer» voir les paragraphes « principe de Huygens - Fresnel » et « contribution de Fraunhofer » du chap. de la leçon « Signaux physiques (PCSI) » où on considère que chaque point de la surface dioptrique ou réfléchissante atteint par l'onde plane incidente peut être considéré comme une source secondaire réémettant une ondelette de Huygens, l'ensemble des ondelettes interférant pour donner une onde résultante également plane le schéma d'explication du paragraphe « précité » ayant été fait avec une onde plane incidente normale, l'onde réfractée à l'exclusion des bords est plane également normale mais la justification est indépendante de cette particularité et la réfraction peut être remplacée sans inconvénient par une réflexion ;
Modèle:AlChristian Huygens (1629 – 1695) ou Christian Huyghens mathématicien, astronome et physicien néerlandais est essentiellement connu pour sa théorie ondulatoire de la lumière.
Modèle:AlAugustin Fresnel (1788 – 1827) physicien français, considéré comme le fondateur de l'optique moderne, a expliqué tous les phénomènes optiques connus de son temps dans le cadre de la théorie ondulatoire de la lumière.
Modèle:AlJoseph von Fraunhofer (1787 – 1826) opticien et physicien allemand est, entre autres, inventeur du spectroscope avec lequel il repéra les raies du spectre solaire. - ↑ 44,0 et 44,1 Le pinceau est parallèle car, bien que l'« O.P.H. réfractée ou réfléchie» ait également une expansion limitée dans l'espace, on est dans le cadre de l'approximation de l'optique géométrique négligeant tout phénomène de diffraction.
- ↑ En supposant que le M.T.H.I. Milieu Transparent Homogène Isotrope limité par la surface réfléchissante est d'indice .
- ↑ Il est nécessaire que les angles et soient de signe contraire pour que « le retard de phase de l'onde en sur celle de l'onde en du rayon corresponde à un retard de phase de l'onde en sur celle de l'onde en du rayon » il suffirait de faire un schéma avec et tous deux positifs pour se rendre compte que le retard de phase de l'onde en sur celle de l'onde en correspondrait à une avance de phase de l'onde en sur celle de l'onde en ce qui est effectivement à rejeter.
- ↑ 47,0 47,1 et 47,2 Condition Nécessaire.
- ↑ Mais en pratique l'égalité n'est jamais à considérer ; si on faisait un grand nombre d'expériences en donnant à l'angle d'incidence la valeur de l'angle limite plus exactement on souhaiterait une valeur vraie égale à l'angle limite mais la valeur donnée serait une valeur proche par défaut ou par excès, la donne étant aléatoire, on trouverait que des cas correspondent à une réflexion totale, les autres à une réflexion partielle accompagnant une réfraction rasante.
- ↑ Dans les premiers appareils photographiques « non réflex », le photographe regardait à travers un viseur mais le trajet de la lumière reçue par son œil n'était pas le même que celui de la lumière devant réaliser l'impression sur la pellicule d'où un cadrage non assuré surtout pour les portraits ; avec l'arrivée des appareils photographiques « réflex », la lumière reçue par l'œil passe d'abord par les lentilles avant d'être réfléchie totalement en direction du viseur à l'aide d'un prisme à réflexion totale ou d'un miroir plan incliné de , ceci permettant de faire un cadrage correct de la photographie à prendre mais bien sûr le prisme à réflexion totale ou le miroir plan incliné à est retiré du trajet de la lumière lors de la prise d'impression.
- ↑ La section droite du prisme étant un triangle rectangle isocèle les angles non droits sont égaux à .
- ↑ Cette condition, non très exigeante, n'est certainement pas réalisée pour n'importe quel rayon incident pénétrant par la face d'entrée mais elle l'est assurément pour la grande majorité des rayons incidents avec une légère perte de puissance correspondant aux quelques rayons qui ne subiraient pas la réflexion totale.
- ↑ Sur la figure seule l'âme a été représentée.