Outils mathématiques pour la physique (PCSI)/Divers repérages d'un point dans l'espace
Repérage intrinsèque d'un point dans l'espace
Repérage cartésien d'un point dans l'espace
Choix d'un repère cartésien
Modèle:AlUn corps physique fixe dans l'espace ayant été défini comme « référentiel d'espace » , on lui associe un « repère cartésien » c.-à-d.
Modèle:AlModèle:Transparentune « origine » fixe dans et
Modèle:AlModèle:Transparentune « base orthonormée » usuellement directe[2] [3] également fixe dans ,
Modèle:AlModèle:Transparentchaque vecteur de base orientant un axe passant par à savoir :
Modèle:AlModèle:Transparent« orienté par » axe des abscisses,
Modèle:AlModèle:Transparent« orienté par » axe des ordonnées et
Modèle:AlModèle:Transparent« orienté par » axe des cotes.
Coordonnées cartésiennes d'un point
Modèle:AlLe vecteur position de se décomposant dans la base cartésienne selon , « définissent les coordonnées cartésiennes du point »[4]
Modèle:AlModèle:Transparent abscisse, ordonnée et cote.
Modèle:Propriété
Repérage cylindro-polaire (ou cylindrique) d'un point dans l'espace
Principe du repérage cylindro-polaire (ou cylindrique) d'un point

Modèle:AlAppelant le projeté orthogonal de sur l'axe et
Modèle:AlModèle:Transparent celui de sur le plan ,
Modèle:Alon définit le repérage cylindro-polaire ou cylindrique de en conservant la localisation de par sa cote mais
Modèle:AlModèle:Transparenten modifiant celle de relativement à son repérage cartésien,
Modèle:AlModèle:Transparent étant repéré par la distance le séparant de
Modèle:Transparentet par l'angle orienté [5] que fait
Modèle:Transparent avec ;
Modèle:Alle nom complet du repérage est repérage cylindro-polaire ou cylindrique d'axe .
Modèle:AlVoir schéma en perspective ci-contre.
Coordonnées cylindro-polaires et base locale associée d'un point

Modèle:AlLes coordonnées cylindro-polaires ou cylindriques de sont avec
Modèle:AlModèle:Transparent«» sa « coordonnée radiale »[6],
Modèle:AlModèle:Transparent«» sa « coordonnée angulaire »[7] et
Modèle:AlModèle:Transparent«» sa cote ;
Modèle:Alil faut savoir remplacer le schéma en perspective par deux schémas de projection, l'un dans le demi-plan méridien et
Modèle:AlModèle:Transparentl'autre en vue de dessus
Modèle:AlModèle:Transparentvoir ci-contre.
Modèle:AlOn définit la base « cylindro-polaire » ou cylindrique liée à « orthonormée directe[2] » avec
Modèle:AlModèle:Transparentle 1er vecteur de la base ,
Modèle:AlModèle:Transparentle 2nd vecteur de la base dans le plan « directement au précédent »[8] on peut encore le définir par et
Modèle:AlModèle:Transparentle 3ème vecteur de la base identique au 3ème vecteur de la base cartésienne ;
Modèle:Alcette base est liée à car les deux 1ers vecteurs de la base dépendent de : le 1er est appelé « vecteur radial »,
Modèle:AlModèle:Transparentle 2nd Modèle:Transparent« vecteur orthoradial » et
Modèle:AlModèle:Transparentle 3ème constant Modèle:Transparent« vecteur axial »[9].
Composantes cylindro-polaires du vecteur position d'un point
Modèle:AlLe vecteur position du point s'écrivant dans la base cylindro-polaire liée à selon «»[10],
Modèle:Alon en déduit que les composantes radiale et axiale du vecteur position, respectivement et , sont identiques aux coordonnées radiale et axiale du point,
Modèle:AlModèle:Transparentalors que la composante orthoradiale du vecteur position diffère de la coordonnée angulaire du point[11].
Lien entre repérages cylindro-polaire et cartésien d'un point
Repérage cylindro-polaire en fonction du repérage cartésien
Modèle:AlVecteurs de base cylindro-polaireou cylindriqueen fonction des vecteurs de base cartésienne : , le 3ème vecteur étant le même ou encore
Modèle:AlModèle:Transparent[12].
Modèle:AlCoordonnées cylindro-polairesou cylindriquesen fonction des coordonnées cartésiennes : [13], la 3ème cordonnée étant la même.
Repérage cartésien en fonction du repérage cylindro-polaire
Modèle:AlVecteurs de base cartésienne en fonction des vecteurs de base cylindro-polaireou cylindrique : , le 3ème vecteur étant le même ou encore
Modèle:AlModèle:Transparent[12].
Modèle:AlCoordonnées cartésiennes en fonction des coordonnées cylindro-polairesou cylindriques : , la 3ème cordonnée étant la même.
Modèle:AlRemarque : Le repérage cylindro-polaire ou cylindrique se suffit à lui-même, il ne faut jamais sauf dans de très rares cas transformer le repérage cylindro-polaire en repérage cartésien ;
Modèle:AlModèle:Transparentsi on utilise le repérage cylindro-polaire c'est que le traitement dans ce repérage est plus simple que dans le repérage cartésien, et il peut être nettement plus simple !
Repérage sphérique d'un point dans l'espace
Principe du repérage sphérique d'un point

Modèle:AlAppelant le projeté orthogonal de sur l'axe et
Modèle:AlModèle:Transparent celui de sur le plan , on définit le demi-plan méridien contenant et [14] et
Modèle:AlModèle:Transparenton repère ce demi-plan méridien par l'angle orienté [15] qu'il fait avec
Modèle:AlModèle:Transparentle demi-plan méridien de référence analogue géographique
Modèle:AlModèle:Transparentde la longitude, puis
Modèle:AlModèle:Transparenton repère dans ce demi-plan méridien
Modèle:AlModèle:Transparentpar la distance séparant de analogue géographique
Modèle:AlModèle:Transparentde l'altitude augmentée du rayon de la Terre et
Modèle:AlModèle:Transparentpar l'angle orienté [16] que fait le vecteur position de
Modèle:AlModèle:Transparentavec l'axe analogue géographique
Modèle:AlModèle:Transparentde la colatitude ;
Modèle:Alon obtient ainsi le repérage sphérique de pôle et[17] d'axe ,
Modèle:AlModèle:Transparentce repérage utilisant une distance non algébrisée et deux angles orientés.
Modèle:AlVoir schéma en perspective ci-contre.
Coordonnées sphériques et base locale associée d'un point

Modèle:AlLes coordonnées sphériques de sont avec «» son « rayon polaire»[18],
Modèle:AlModèle:Transparent«» sa « colatitude »[19] et
Modèle:AlModèle:Transparent«» sa « longitude »[20] ;
Modèle:Alil faut savoir remplacer le schéma en perspective par deux schémas de projection dans le demi-plan méridien et
Modèle:AlModèle:Transparenten vue de dessus [21],
Modèle:AlModèle:Transparentvoir ci-contre la base cylindro-polaire y est
Modèle:AlModèle:Transparentrappelée en marron.
Modèle:AlOn définit la base « sphérique » liée à orthonormée directe[2] avec
Modèle:AlModèle:Transparentle 1er vecteur de la base ,
Modèle:AlModèle:Transparentle 2nd vecteur de la base dans le demi-plan méridien « directement au précédent »[22] on peut encore le définir par
Modèle:AlModèle:Transparentavec le 3ème vecteur de la base et
Modèle:AlModèle:Transparentle 3ème vecteur de la base au demi-plan méridien et orientant ce dernier[23] soit encore [24] ;
Modèle:Alcette base est liée à car les deux 1ers vecteurs de la base dépendent de et , le 1er est appelé « vecteur radial »,
Modèle:AlModèle:Transparentle 2nd Modèle:Transparent « vecteur orthoradial »[25]Modèle:,[26] et
Modèle:AlModèle:Transparentle 3ème vecteur de la base sphérique dépend de seul, le 3ème Modèle:Transparent « vecteur longitudal »[27].
Composantes sphériques du vecteur position d'un point
Modèle:AlLe vecteur position du point s'écrivant dans la base sphérique liée à selon «»[28],
Modèle:Alon en déduit que la composante radiale du vecteur position , est identique à la coordonnée radiale du point,
Modèle:AlModèle:Transparentalors que les composantes orthoradiale et longitudale du vecteur position et diffèrent des coordonnées angulaires et du point[29].
Interprétation géographique du repérage sphérique d'un point
Modèle:AlPour un repérage sphérique de pôle et[17] d'axe , l'axe est identifié à l'axe « pôle Sud - pôle Nord » de la Terre, « est l'altitude augmentée du rayon de la Terre »,
Modèle:AlModèle:Transparent« le vecteur unitaire vertical »,
Modèle:AlModèle:Transparent« la colatitude »[30],
Modèle:AlModèle:Transparent« le vecteur unitaire horizontal dirigé vers le Sud »,
Modèle:AlModèle:Transparent« la longitude » et
Modèle:AlModèle:Transparent« le vecteur unitaire horizontal dirigé vers l'Est ».
Lien entre repérages sphérique et cylindro-polaire d'un point
Repérage sphérique en fonction du repérage cylindro-polaire
Modèle:AlVecteurs de base sphérique en fonction des vecteurs de base cylindro-polaireou cylindrique : [24] ou encore
Modèle:AlModèle:Transparent[12]Modèle:,[24].
Modèle:AlCoordonnées sphériques en fonction des coordonnées cylindro-polairesou cylindriques : [31] suffisant pour déterminer .
Repérage cylindro-polaire en fonction du repérage sphérique
Modèle:AlVecteurs de base cylindro-polaireou cylindriqueen fonction des vecteurs de base sphérique : [24] ou encore
Modèle:AlModèle:Transparent[12]Modèle:,[24].
Modèle:AlCoordonnées cylindro-polairesou cylindriquesen fonction des coordonnées sphériques : [31].
Modèle:AlRemarque : Le repérage sphérique se suffit à lui-même, a priori il est inutile de transformer le repérage sphérique en repérage cylindro-polaire ou cylindrique[32] ;
Modèle:AlModèle:Transparentsi on utilise le repérage sphérique c'est que le traitement dans ce repérage est plus simple que dans le repérage cylindro-polaire,
Modèle:AlModèle:Transparentexemple d'un déplacement sur une sphère seules et varient !
Lien entre repérages sphérique et cartésien d'un point
Repérage sphérique en fonction du repérage cartésien
Modèle:AlVecteurs de base sphérique en fonction des vecteurs de base cartésienne : [33].
Modèle:AlCoordonnées sphériques en fonction des coordonnées cartésiennes : [34]Modèle:,[35], suffisant pour déterminer .
Repérage cartésien en fonction du repérage sphérique
Modèle:AlVecteurs de base cartésienne en fonction des vecteurs de base sphérique : on décompose les vecteurs de base cartésienne dans la base cylindro-polaire puis
Modèle:AlModèle:Transparentla base cylindro-polaire dans la base sphérique .
Modèle:AlCoordonnées cartésiennes en fonction des coordonnées sphériques : [36].
Modèle:AlRemarque : Le repérage sphérique se suffit à lui-même, il n'est jamais utile de transformer le repérage sphérique en repérage cartésien ;
Modèle:AlModèle:Transparentsi, dans certains cas, substituer le repérage cylindro-polaire au repérage sphérique s'impose, il ne sera jamais intéressant de remplacer le repérage sphérique par le repérage cartésien.
Vecteur déplacement élémentaire d'un point
Définition intrinsèque
Modèle:AlLa notion de vecteur déplacement d'un point à partir d'une position quelconque nécessite de préciser la position finale du déplacement, le vecteur déplacement obtenu s'écrivant ;
Modèle:Alsi la position finale reste proche de la position initiale , on substitue la notation à celle de et le vecteur déplacementest qualifié de « petit » ;
Modèle:Alpour infiniment proche de suivant une direction d'approche fixée, on substitue la notation à celle de et le vecteur déplacementest qualifié d'élémentaire.
Modèle:AlLe vecteur déplacement élémentaire à partir d'une position quelconque en suivant une direction fixée peut être considéré aussi comme obtenu en suivant une courbe passant par [37] ;
Modèle:Alen conclusion la définition intrinsèque du vecteur déplacement élémentaire à partir d'une positions'identifie à
Modèle:AlModèle:Transparentcelle du vecteur déplacement élémentaire d'un point le long d'une courbe vue dans le chap. de la leçon « Outils mathématiques pour la physique (PCSI) »[38] ;
Modèle:AlModèle:Transparenton y a défini le vecteur déplacement élémentaire le long d'une courbe continue comme la différentielle du vecteur position dont les valeurs successives décrivent la courbe soit
Modèle:AlModèle:Transparent ou simplement «»[39] ;
Modèle:AlModèle:Transparentle vecteur déplacement élémentaire le long de la courbe est tangent à la courbe en , dans la mesure où [40].
Composantes cartésiennes du vecteur déplacement élémentaire d'un point
Expression du vecteur déplacement élémentaire d'un point en repérage cartésien
Modèle:AlPour établir l'expression du vecteur déplacement élémentaire en repérage cartésien nous différencions le vecteur position exprimé dans ce repérage, sans particulariser le déplacement suivant une courbe, soit , les vecteurs de la base cartésienne étant constants leur différentielle est nulle. Modèle:Proposition
Détermination géométrique des composantes cartésiennes du vecteur déplacement élémentaire d'un point
Modèle:AlPour créer un déplacement élémentaire du point en repérage cartésien, on envisage successivement un déplacement élémentaire le long de chaque vecteur de base, le vecteur déplacement élémentaire du point étant la somme de ces trois déplacements élémentaires, ainsi :
- suivant , on se déplace selon la droite passant par et à c.-à-d. d'équations et du « petit segment élémentaire » de longueur algébrique d'où ,
- suivant , on se déplace selon la droite passant par et à c.-à-d. d'équations et du « petit segment élémentaire » de longueur algébrique d'où ,
- suivant , on se déplace selon la droite passant par et à c.-à-d. d'équations et du « petit segment élémentaire » de longueur algébrique d'où ,
Modèle:Alle vecteur déplacement élémentaire étant finalement se réécrit , ses composantes cartésiennes étant donc .
Application au vecteur déplacement élémentaire le long d'une courbe
Modèle:AlConsidérons la parabole d'équations cartésiennes [41] et différencions ces équations : on obtient alors et
Modèle:AlModèle:Transparentle vecteur déplacement élémentaire le long de la parabole s'explicite en fonction de l'élément différentiel selon
Modèle:AlModèle:Transparent«»[42] ;
Modèle:AlModèle:Transparentd'une part il n'existe aucun point de la parabole où le vecteur déplacement élémentaire est nul,
Modèle:AlModèle:Transparentd'autre part, pour , la composante vectorielle sur est toujours dans le sens de et
Modèle:AlModèle:Transparentla composante vectorielle sur est de sens contraire à pour ,
Modèle:AlModèle:Transparents'annule pour et
Modèle:AlModèle:Transparentest dans le sens de pour ,
Modèle:AlModèle:Transparentde norme d'autant plus grande que l'est[43]
Composantes cylindro-polaires du vecteur déplacement élémentaire d'un point
Calcul préliminaire
Modèle:AlPour établir l'expression du vecteur déplacement élémentaire en repérage cylindro-polaire ou cylindrique nous différencions le vecteur position exprimé dans ce repérage, sans particulariser le déplacement suivant une courbe, soit [44].
Différentielle des vecteurs de base cylindro-polaire
Modèle:AlPour déterminer la différentielle des vecteurs de base cylindro-polaire, il faut les décomposer dans la base cartésienne de façon à faire apparaître explicitement l'angle dont ils dépendent soit
Modèle:AlModèle:Transparent[45] ;
Modèle:Alon utilise [46] avec les dérivées par rapport à des deux 1ers vecteurs de base égales à [47]Modèle:,[48] soit :
Modèle:Proposition
Modèle:AlLe report dans les expressions des différentielles nous conduisent à .
Expression du vecteur déplacement élémentaire d'un point en repérage cylindro-polaire
Modèle:AlOn reporte l'expression de dans celle de obtenue en calcul préliminaire et on trouve . Modèle:Proposition
Détermination géométrique des composantes cylindro-polaires du vecteur déplacement élémentaire d'un point
Modèle:AlPour créer un déplacement élémentaire du point en repérage cynlidro-polaire, on envisage successivement un déplacement élémentaire le long de chaque vecteur de base, le vecteur déplacement élémentaire du point étant la somme de ces trois déplacements élémentaires, ainsi :
- suivant , on se déplace selon la demi-droite passant par et à c.-à-d. d'équations et du « petit segment élémentaire » de longueur algébrique d'où
Modèle:Transparent«», - suivant , on se déplace selon le cercle passant par et d'axe c.-à-d. d'équations et du « petit arc élémentaire » de longueur algébrique [49] d'où
Modèle:Transparent«», - suivant , on se déplace selon la droite passant par et à c.-à-d. d'équations et du « petit segment élémentaire » de longueur algébrique d'où
Modèle:Transparent«»,
Modèle:Alle vecteur déplacement élémentaire étant finalement se réécrit «», ses composantes cylindro-polaires étant donc .
Application au vecteur déplacement élémentaire le long d'une courbe connue par ses équations cylindro-polaires
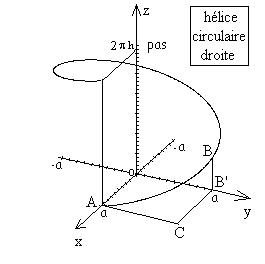
Modèle:AlCi-contre à gauche le tracé d'une hélice circulaire droite[50] d'axe ;
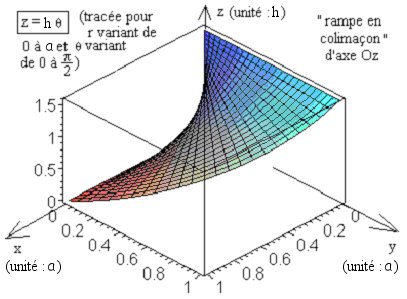
Modèle:Alci-contre à droite le tracé de la surface d'équation cylindro-polaire « cote à l'abscisse angulaire » qui est une des deux équations cylindro-polaires définissant l'hélice circulaire droite[50] d'axe , l'autre surface étant un tuyau cylindrique de révolution d'axe .
Modèle:AlVecteur déplacement élémentaire le long d'une hélice circulaire droite[50] d'axe : Soit l'hélice circulaire d'équations cylindro-polaires «»[51], nous cherchons à déterminer le vecteur déplacement élémentaire du point générique de l'hélice circulaire et pour cela nous différencions les équations de cette dernière : on obtient alors «» et le vecteur déplacement élémentaire le long de l'hélice circulaire peut s'écrire uniquement en fonction de l'élément différentiel selon
Modèle:Al«»[52].
Modèle:AlCommentaires sur le vecteur déplacement le long d'une hélice circulaire droite[50] d'axe : il n'existe aucun point de l'hélice circulaire où le vecteur déplacement élémentaire est nul,
Modèle:AlModèle:Transparentpour , la composante vectorielle sur , est toujours dans le sens de et Modèle:AlModèle:Transparentcelle sur , est de sens contraire à pour [53], et
Modèle:AlModèle:Transparentdans le sens de pour [54],
Modèle:AlModèle:Transparentla norme du vecteur déplacement élémentaire est indépendante de [55]
Modèle:AlQuelques commentaires sur l'hélice circulaire : une hélice circulaire est donc tracée sur un tuyau cylindrique de révolution avec à ;
Modèle:AlModèle:Transparentsi on « développe » le tuyau cylindrique de révolution de façon à ce que sa surface latérale devienne un plan,
Modèle:AlModèle:Transparentl'hélice circulaire se « développe » en une droite c.-à-d. en une courbe de « pente constante »[56] ;
Modèle:AlModèle:Transparentelle est qualifiée de « dextre ou droite » si le cœfficient de proportionnalité entre et est , elle « monte » dans le sens trigonométrique[57]
Modèle:AlModèle:Transparentun observateur placé à l’extérieur la voit, lorsqu'elle est devant lui, « monter de gauche à droite » ;
Modèle:AlModèle:Transparentelle est qualifiée de « senestre ou gauche » si le cœfficient de proportionnalité entre et est , elle « monte » dans le sens anti-trigonométrique[58],
Modèle:AlModèle:Transparentun observateur placé à l’extérieur la voit, lorsqu'elle est devant lui, « monter de droite à gauche » ;
Modèle:AlModèle:Transparenton définit le pas de l'hélice circulaire par la variation de cote correspondant à un tour complet soit
Modèle:AlModèle:Transparentun pas de pour une équation cylindro-polaire de rampe en colimaçon .
Composantes sphériques du vecteur déplacement élémentaire d'un point
Calcul préliminaire
Modèle:AlPour établir l'expression du vecteur déplacement élémentaire en repérage sphérique nous différencions le vecteur position exprimé dans ce repérage, sans particulariser le déplacement suivant une courbe, soit [59].
Détermination géométrique des composantes sphériques du vecteur déplacement élémentaire d'un point
Modèle:AlPour créer un déplacement élémentaire du point en repérage sphérique, on envisage successivement un déplacement élémentaire le long de chaque vecteur de base, le vecteur déplacement élémentaire du point étant la somme de ces trois déplacements élémentaires, ainsi :
- suivant , on se déplace selon la demi-droite passant par et à [60] c.-à-d. d'équations et du « petit segment élémentaire » de longueur algébrique d'où
Modèle:Transparent«», - suivant , on se déplace selon le demi-cercle méridien passant par [61] c.-à-d. d'équations et du « petit arc élémentaire » de longueur algébrique [62] d'où
Modèle:Transparent«», - suivant , on se déplace selon le cercle « parallèle » passant par [63] c.-à-d. d'équations et du « petit arc élémentaire » de longueur algébrique [64] d'où Modèle:Transparent«»,
Modèle:Alle vecteur déplacement élémentaire étant finalement se réécrit «»,
Modèle:AlModèle:Transparentses composantes sphériques étant .
Expression du vecteur déplacement élémentaire d'un point en repérage sphérique
Complément : différentielle des vecteurs de base sphérique
Modèle:AlNous utilisons la définition de la différentielle d'une fonction vectorielle de l'espace utilisant la notion de dérivées partielles vue chap. de la leçon « Outils mathématiques pour la physique (PCSI) » d'où
Modèle:AlModèle:Transparent«»[65].
Détermination des dérivées partielles du 1er vecteur de base sphérique

Modèle:AlPour cela on utilise la décomposition de dans la base cylindro-polaire [66] soit :
Modèle:Al«» «»[67] d'où finalement le vecteur unitaire du demi-plan méridien directement à c.-à-d. , en conclusion on a «» ;
Modèle:Al«» «»[68] ou, étant un vecteur unitaire du plan équatorial [69], en conclusion on a «».
Détermination des dérivées partielles du 2nd vecteur de base sphérique
Modèle:AlPour cela on utilise la décomposition de dans la base cylindro-polaire [66] soit :
Modèle:Al«» «»[67] d'où finalement le vecteur unitaire du demi-plan méridien directement à Modèle:Nobr , en conclusion on a «» ;
Modèle:Al«»[12] «»[68] ou, sachant que [69], on en déduit en conclusion «».
Détermination de la dérivée du 3ème vecteur de base sphérique
Modèle:Al étant un vecteur unitaire du plan équatorial et dérivant par rapport à l'angle qu'il fait avec la direction fixe de ce plan «»[69] ;
Modèle:Alil reste alors à décomposer dans la base sphérique[70], ce qui donne d'où «».
Explicitation des différentielles des vecteurs de base sphérique
Complément : détermination du vecteur déplacement élémentaire d'un point en repérage sphérique par utilisation de la différentielle du 1er vecteur de base sphérique
Modèle:AlReprenant le résultat du calcul préliminaire
et y reportant
nous trouvons effectivement
Application au vecteur déplacement élémentaire le long d'une courbe connue par ses équations sphériques

Modèle:AlConsidérons la loxodromie de sphère de pente par rapport aux parallèles tracée en rouge sur le schéma ci-contre d'équations sphériques [73], pour établir l'expression du vecteur déplacement élémentaire le long de la loxodromie de sphère au point , nous différencions ses équations et obtenons alors «»[74]Modèle:,[75] ou ou encore [76] soit finalement «», d'où le vecteur déplacement élémentaire le long de la loxodromie de sphère en fonction de l'élément différentiel «»[77] Modèle:Nobr pas oublier soit finalement, après une transformation élémentaire, «»[78] ;
Modèle:AlCommentaires sur le vecteur déplacement élémentaire le long de la loxodromie de sphère de pentepar rapport aux Modèle:Nobr
Modèle:AlModèle:Transparentil n'existe aucun point de la loxodromie sphérique
Modèle:AlModèle:Transparentde vecteur déplacement élémentaire nul,
Modèle:AlModèle:Transparentpour , la composante vectorielle sur , , est toujours dans le sens contraire de c.-à-d. vers le Nord et
Modèle:AlModèle:Transparentcelle sur , , est dans le sens de c.-à-d. vers l'Est,
Modèle:AlModèle:Transparentpour , la composante vectorielle sur , , est toujours dans le sens de c.-à-d. vers le Sud et
Modèle:AlModèle:Transparentcelle sur , , est en sens contraire de c.-à-d. vers l'Ouest ;
Modèle:AlModèle:Transparentla norme ainsi que la pente dans le plan tangent à la sphère du vecteur déplacement élémentaire sont indépendantes de [79]
Modèle:AlRemarque : Pour mieux faire apparaître la loxodromie de sphère, sa projetée sur le plan équatorial de la sphère a été tracée en vert, elle porte le nom de « spirale de Poinsot bornée »[72].
Repérages d'une courbe dans l'espace
Repérages cartésien, cylindro-polaire ou sphérique d'une courbe
Modèle:AlDans un repérage cartésien, cylindro-polaire ou sphérique, il faut deux équations pour caractériser une courbe, pour mémoire revoir les trois exemples précédemment exposés :



- la parabole d'équations «»[41] repérée en cartésien ci-contre à gauche,
Modèle:Transparentla 1ère équation «» caractérisant un cylindre parabolique de génératrices à et
Modèle:Transparentla 2nde «» le plan ; - l'hélice circulaire d'équations «»[51] repérée en cylindro-polaire Modèle:Nobr à droite,
Modèle:Transparentla 1ère équation «» caractérisant un tuyau cylindrique de révolution d'axe et de rayon ,
Modèle:Transparentla 2nde «» une surface sans nom mathématique mais que l'on pourrait appeler « rampe en colimaçon » constituée de demi-droites au plan issues d'un point de l'axe de cote plus ou moins élevée suivant la valeur de l'abscisse angulaire fonction de ; - la loxodromie sphérique de pente par rapport aux parallèles, d'équations
Modèle:Al«»[73] repérée en sphérique
Modèle:Alci-contre à droite,
Modèle:AlModèle:Transparentla 1ère équation «» caractérisant une sphère de centre
Modèle:Al dont le rayon est et
Modèle:AlModèle:Transparentla 2nde «» une surface
Modèle:Alsans nom mathématique constituée de demi-droites issues de
Modèle:Alplus ou moins inclinées suivant la valeur de la colatitude
Modèle:Alla longitude étant fonction de la colatitude .
Repérage paramétrique d'une courbe
Modèle:AlEn repérage paramétrique, qu'il soit cartésien, cylindro-polaire ou sphérique, il faut trois équations paramétriques pour caractériser une courbe[81] ;
Modèle:AlModèle:Transparentci-dessous un exemple de courbe en repérage paramétrique cartésien[82] :

Modèle:AlSoient les trois équations paramétriques cartésiennes de la courbe «», nous nous proposons d'établir
Modèle:AlModèle:Transparentle caractère plan de la courbe et
Modèle:AlModèle:Transparentla nature de cette dernière ;
- pour démontrer la nature plane de la courbe il faut trouver une relation affine entre , et en éliminant le paramètre
Modèle:Transparententre les équations paramétriques affines et soit «» en
Modèle:Transparentreportant dans , ou «» équation cartésienne
Modèle:Transparentd'un plan,
Modèle:Transparent« plan à de trace dans le plan , la droite d'équation
Modèle:Transparentpassant par le point »[83] d'où la nature plane de ; - pour déterminer la nature de la courbe il faut établir une 2ème équation cartésienne de , la 1ère étant celle du plan précédent,
Modèle:Transparentpour cela, éliminer le paramètre entre les équations paramétriques et soit
Modèle:Transparent«» en reportant dans , ou
Modèle:AlModèle:Transparent«»[84] équation cartésienne d'un cylindre parabolique de génératrices à ;
Modèle:Transparentles deux équations cartésiennes de la courbe sont «» est l'intersection du cylindre parabolique de génératrices à et
Modèle:AlModèle:Transparentdu plan à passant par le point ,
Modèle:Transparenten conclusion étant l'intersection d'un cylindre parabolique de génératrices à et d'un plan à est une parabole[85].
Modèle:AlRemarque : utiliser la 2ème équation paramétrique pour éliminer le paramètre était possible mais aurait été particulièrement maladroit en effet cela aurait conduit à «» soient,
Modèle:AlModèle:Transparentpar report, les deux équations cartésiennes «» dont aucune n'est une relation affine bien que la courbe soit plane, elle est déterminée ici à l'aide de cette
Modèle:AlModèle:Transparentélimination maladroite par l'intersection de deux surfaces non planes ;
Modèle:AlModèle:Transparentles deux équations cartésiennes obtenues en éliminant le paramètre à l'aide de la 2ème équation paramétrique se réécrivant «» «»
Modèle:AlModèle:Transparentne permettent pas de déterminer le caractère plan de la courbe ainsi que
Modèle:AlModèle:Transparentla nature de cette dernière
Modèle:AlModèle:Transparentcar elle est l'intersection de deux cylindres paraboliques de génératrices respectivement à et à
Modèle:AlModèle:Transparentdont l'intersection nécessiterait une étude plus poussée.
Choix du système de coordonnées adapté au problème
Modèle:AlLe plus souvent le système de coordonnées est imposé par le texte de l'exercice et a priori vous ne devez en aucun cas en changer,
Modèle:AlModèle:Transparentmais si l'initiative du choix vous est laissée, vous adoptez le système adapté au problème à savoir :
- le système de coordonnées cylindro-polairesou cylindriques d'axe pour un problème ayant l'« invariance par symétrie de révolution d'axe» c.-à-d. un problème invariant par rotation autour de l'axe , ne dépendant donc pas de l'abscisse angulaire , par exemple l'écoulement de l'eau à l'intérieur d'un tuyau cylindrique de révolution d'axe ou la marche d'une fourmi sur la surface latérale extérieure de ce tuyau cylindrique de révolution ou pour un problème ne possédant pas cette invariance mais pour lequel le rayon polaire[86] ne varie pas par exemple la montée d'une fourmi sur une hélice circulaire, courbe tracée sur un tuyau cylindrique de révolution,
- le système de coordonnées sphériques de pôle pour un problème possédant l'« invariance par symétrie sphérique de centre» c.-à-d. un problème invariant par rotation autour de n'importe quel axe passant par , ne dépendant donc pas de la colatitude et de la longitude relativement à un axe quelconque choisi comme axe , par exemple en restant dans le cadre de la « mécanique classique »[87] le « mouvement de l'électron dans un atome d'hydrogène autour de son noyau »[88] ou le « mouvement d'un satellite autour de la Terre » ou la marche d'une fourmi sur un ballon de Modèle:Nobr ou pour un problème ne possédant pas cette invariance mais pour lequel le rayonpolairene varie pas par exemple la marche d'une fourmi sur un ballon de handball en rotation autour d'un axe vertical, la rotation rendant la marche moins assurée au niveau équatorial du ballon que près d'un pôle c.-à-d. que les conditions de maintien sur le ballon dépendent de la colatitude de la fourmi sur le ballon, maintien plus difficile au niveau équatorial qu'à un des pôles[89],
- le système de coordonnées cartésiennes pour un problème ne possédant aucune des invariances précédentes et pour lequel on cherche la description du mouvement d'un objet relativement à des plans fixes par exemple le drop d'un ballon de rugby pour savoir si ce mouvement va passer au-dessus de la barre transversale.
En complément, repérage de Frenet d'un point sur une courbe
Modèle:AlL'introduction du repérage de Frenet[90] est présentée « en complément »[91], toutefois il est difficile de s'en passer car c'est le seul repérage introduisant les notions utilisées dans la vie quotidienne comme la « longueur parcourue sur une courbe » ou la « vitesse lue sur un tachymètre » ou l'« accélération tangentielle le long d'une courbe »[92].
Rappel, notion d'abscisse curviligne d'un point et de vecteur unitaire tangentiel, 1er vecteur de la base locale de Frenet associée
Modèle:AlCes notions ayant déjà été introduites dans les paragraphes « abscisse curviligne d'un point sur une courbe continue » et
Modèle:AlModèle:Transparent« définition du vecteur déplacement élémentaire le long d'une courbe continue à l'aide de la base locale deFrenet »[90]
Modèle:AlModèle:Transparentdu chap. de la leçon « Outils mathématiques pour la physique (PCSI) »,
Modèle:AlModèle:Transparentseules les grandes lignes sont rappelées ci-dessous :

Modèle:AlSur une courbe continue plane ou gauche, on choisit arbitrairement un sens «» et
Modèle:AlModèle:Transparentune « origine » de mesure des abscisses curvilignes ;
Modèle:AlModèle:Transparentle « point générique » de est repéré par son « abscisse curviligne » longueur
Modèle:AlModèle:Transparentalgébrique parcourue dans le sens «» sur à partir de [93] ;
Modèle:AlModèle:Transparenton définit, en tout point non anguleux[94] de , un vecteur unitaire tangent à en
Modèle:AlModèle:Transparentorienté dans le sens «»
Modèle:AlModèle:Transparentappelé « vecteur unitaire tangentiel » et constituant
Modèle:AlModèle:Transparentle « 1er vecteur de la base locale de Frenet »[90] ;
Modèle:AlModèle:Transparentmathématiquement la relation caractérise la courbe et
Modèle:AlModèle:Transparentreprésente son « équation vectorielle paramétrique » ;
Modèle:AlModèle:Transparentla définition mathématique du 1er vecteur de base de Frenet[90] équivalente à la définition précédente
Modèle:AlModèle:Transparentest «» c.-à-d. que
Modèle:AlModèle:Transparentle vecteur unitaire tangentiel peut être obtenu en dérivant par rapport l'équation vectorielle paramétrique de la courbe .
Notion de cercle osculateur en un point d'une courbe plane, centre et rayon de courbure en ce point
Modèle:AlParmi tous les cercles du plan de la courbe lui étant tangents en , le cercle osculateur à la courbe en est celui qui est « localement le plus proche de la courbe »[95]Modèle:,[96].
Modèle:AlCas particuliers : si le point est un point d'inflexion de la courbe, le cercle osculateur est la tangente elle-même c.-à-d. un cercle de rayon infini,
Modèle:AlModèle:Transparentsi la courbe est un cercle, le cercle osculateur en chacun de ses points est le cercle lui-même et
Modèle:AlModèle:Transparentsi la courbe est une droite, le cercle osculateur en chacun de ses points est la droite elle-même c.-à-d. un cercle de rayon infini.
Modèle:AlAutres définitions : le centre du cercle osculateur à la courbe en définit le centre de courbure de en et
Modèle:AlModèle:Transparentson rayon c.-à-d. , définit le rayon de courbure[97] de en .
Modèle:AlPropriété : Il existe une seule courbe plane à rayon de courbure constant c'est le cercle.
Modèle:AlExemple : La comparaison des rayons de courbure d'une courbe plane en ses différents points se fait visuellement de façon relativement aisée, par exemple,
Modèle:AlModèle:Transparentsi on considère la parabole d'équation cartésienne dans le plan , , de sommet et de direction asymptotique , la concavité étant tournée vers les ,
Modèle:AlModèle:Transparenton remarque aisément que le rayon de courbure est minimale au sommet et
Modèle:AlModèle:Transparentqu'il est d'autant plus grand que le point s'éloigne du sommet
Modèle:AlModèle:Transparentle rayon de courbure tendant vers l'infini pour s'éloignant à l'infini du sommet.
Notion de plan et de cercle osculateurs en un point d'une courbe gauche, centre et rayon de courbure en ce point
Modèle:AlParmi tous les plans tangents en à une courbe gauche , le plan osculateur de en est celui qui est « localement le plus proche de la courbe »[98]Modèle:,[99] ; cette détermination est encore applicable à une courbe plane mais elle est d'un intérêt limité car le plan osculateur d'une courbe plane en chacun de ses points est le plan de la courbe.
Modèle:AlParmi tous les cercles tangents à la courbe gauche en dans le plan osculateur de celle-ci en , le cercle osculateur est celui qui est « localement le plus proche de la courbe »[95] ;
Modèle:Alon définit alors de même que pour une courbe plane : le centre de courbure de en comme le centre du cercle osculateur à en et
Modèle:AlModèle:Transparentle rayon de courbure de en comme le rayon du cercle osculateur c.-à-d. .
Modèle:AlPropriété : Il existe une seule courbe gauche à rayon de courbure constant c'est l'hélice circulaire.
2ème et 3ème vecteurs de la base locale de Frenet associée à un point de la courbe étudiée
2ème vecteur de la base de Frenet associée à un point de la courbe : vecteur unitaire normal principal
Modèle:AlLe 2ème vecteur de base locale de Frenet[90] en un point de la courbe , noté et appelé « vecteurunitairenormal principal » ou simplement « vecteur normal » pour une courbe plane
Modèle:AlModèle:Transparentest le « vecteur unitaire porté par la normale principale » à en c.-à-d. la direction où est
Modèle:AlModèle:Transparentle centre de courbure[100] et
Modèle:AlModèle:Transparentde sens dirigé vers le centre de courbure .
3ème vecteur de la base de Frenet associée à un point de la courbe : vecteur unitaire normal secondaire
Modèle:AlLe 3ème vecteur de base locale de Frenet[90] en un point de la courbe , noté et appelé « vecteurunitairenormal secondaire »
Modèle:AlModèle:Transparentest le « vecteur unitaire porté par la normale secondaire » à en c.-à-d. la direction au plan osculateur
Modèle:AlModèle:Transparentà en [101] et
Modèle:AlModèle:Transparentde sens tel que la baseest directe[2] ;
Modèle:AlModèle:Transparentles angles du plan osculateur à en sont orientés par le vecteur normal secondaire[102] ;
Modèle:AlModèle:Transparentune définition équivalente du vecteur normal secondaire est «».
Rappel, composante de Frenet du vecteur déplacement élémentaire d'un point de la courbe étudiée
Modèle:AlÉtablissement par interprétation géométrique du vecteur déplacement élémentaire d'un point le long d'une courbe continue :
Modèle:AlModèle:Transparent étant repéré sur la courbe par son abscisse curviligne ,
Modèle:AlModèle:Transparentnous envisageons un déplacement élémentaire le long du vecteur unitaire tangentiel de la base locale de Frenet[90] ,
Modèle:AlModèle:Transparentcorrespondant à un « arc de courbe » de longueur algébrique soit finalement
Modèle:AlModèle:Transparent«».
Modèle:AlJustification de la définition mathématique du vecteur unitaire tangentiel : étant le point origine de la définition intrinsèque du vecteur position de [103] et
Modèle:AlModèle:Transparent étant repéré sur la courbe par son abscisse curviligne ,
Modèle:AlModèle:Transparentnous pouvons, a priori, connaître l'équation paramétrique vectorielle de , «» ;
Modèle:AlModèle:Transparentor la différentielle de est le vecteur déplacement élémentaire du point d'où,
Modèle:AlModèle:Transparentpar définition de la différentielle d'une fonction vectorielle d'une variable[46] , identifiable à ,
Modèle:AlModèle:Transparentce qui justifie, a posteriori, la définition mathématique du vecteur unitaire tangentiel de la base de Frenet[90] «».
Définition du rayon de courbure en un point non anguleux d'une courbe plane

Modèle:AlLe vecteur unitaire tangentiel de la base locale de Frenet[90]Modèle:,[104] en , point non anguleux[94], étant de direction repérée par
Modèle:AlModèle:Transparentl'angle qu'elle fait avec la direction fixe du plan de la courbe c.-à-d. «», on en déduit
Modèle:AlModèle:Transparentl'angle algébrisé formé entre les vecteurs unitaires tangentiels en et deux points voisins de la courbe
Modèle:AlModèle:Transparent«» et
Modèle:Alles vecteurs unitaires normaux principaux[105] de Frenet[90]Modèle:,[106] en ces deux points formant le même angle algébrisé [107],
Modèle:Alon définit le rayon de courbure moyen sur l'arc de courbe par «» ;
Modèle:Alon en déduit la définition du rayon de courbure de en [108] comme la limite du rayon de courbure moyen
Modèle:AlModèle:Transparentquand on fait tendre l'écart angulaire vers zéro soit
Modèle:AlModèle:Transparent«»[109] soit finalement
Modèle:Alla définition du rayon de courbure de courbe plane en un point non anguleux[94] «»[110] où [111].
Modèle:AlPropriété : étant l'angle que fait le vecteur unitaire tangentiel de la base de Frenet[90]Modèle:,[104] avec de direction fixe dans le plan de la courbe,
Modèle:AlModèle:Transparentquand on dérive par rapport à , on obtient le vecteur unitaire du plan directement au vecteur unitaire initial[69] c.-à-d.
Modèle:AlModèle:Transparentle vecteur unitaire normal principal[105] de la base locale de Frenet[90]Modèle:,[106] soit encore «»[111].
Définition simultanée du 2ème vecteur de la base locale de Frenet et du rayon de courbure en un point non anguleux d'une courbe quelconque (gauche ou plane)
Établissement de la définition simultanée du 2ème vecteur de la base locale de Frenet et du rayon de courbure en un point non anguleux d'une courbe plane
Modèle:AlAyant établi l'expression du vecteur unitaire tangentiel[104] à la courbe plane en non anguleux[94] en fonction de l'abscisse curviligne de ce dernier
Modèle:AlModèle:Transparent«»[104] où est l'équation paramétrique vectorielle de ,
Modèle:AlModèle:Transparenton dérive par rapport à en remarquant qu'à toute valeur de on peut associer un point unique
Modèle:AlModèle:Transparentque la courbe plane soit ouverte ou fermée et
Modèle:AlModèle:Transparentqu'à tout non anguleux[94] correspond une valeur unique
Modèle:AlModèle:Transparentpermettant de déduire, par transitivité,
Modèle:AlModèle:Transparentqu'à toute valeur de on peut associer une valeur unique
Modèle:AlModèle:Transparentce qui définit la fonction sans avoir besoin de
Modèle:AlModèle:Transparentrestreindre le domaine de définition de ;
Modèle:AlModèle:Transparenton en déduit, par dérivée de fonction composée, «» avec «»[112] et
Modèle:AlModèle:Transparent«»[112] c.-à-d. « courbure
Modèle:AlModèle:Transparentde en »[113]
Modèle:AlModèle:Transparentces deux relations n'étant définies que pour une courbe plane
Modèle:AlModèle:Transparentsoit finalement «»[114].
Énoncé de la définition simultanée du 2ème vecteur de la base locale de Frenet et du rayon de courbure en un point non anguleux d'une courbe gauche
Modèle:AlL'expression donnant la dérivée du vecteur unitaire tangentiel[104] en fonction de l'abscisse curviligne établie pour une courbe plane
[115] est admise pour une courbe gauche et
Modèle:AlModèle:Transparentsert de définition simultanée du vecteur unitaire normal principal[116] et du rayon de courbure à la courbe gauche
[117] en
non anguleux[94] soit
Modèle:AlMode opératoire pour déterminer le rayon de courbure[117] et le vecteur unitaire normal principal[116] en un point non anguleux[94] d'une courbe gauche :
Modèle:AlModèle:Transparent« Connaissant l'expression de relativement à [119], on dérive cette expression et on obtient »,
Modèle:AlModèle:Transparent« on en prend la norme et on obtient la courbure de la courbe[113] en , ou, en inversant, le rayon de courbure de la courbe[117] en , »,
Modèle:AlModèle:Transparent« on en déduit alors le vecteur unitaire normal principal[116] par » ;
Modèle:AlModèle:Transparentenfin « on peut terminer avec la détermination du vecteur unitaire normal secondaire par »[120].
Notes et références
- ↑ Voir l'introduction du paragraphe « produit vectoriel de deux vecteurs » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ 2,0 2,1 2,2 et 2,3 Voir le paragraphe « base directe d'un espace orienté à droite » ainsi que la note « 17 » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ Définissant la « base cartésienne » du repère cartésien.
- ↑ On constate que les coordonnées cartésiennes du point sont par définition les composantes cartésiennes du vecteur position , ceci n'est vrai qu'en repérage cartésien, cela devient faux en repérage local comme cylindro-polaire ou sphérique car les vecteurs de base n'y sont pas choisis fixes.
- ↑ Orienté par un vecteur unitaire au plan c.-à-d. par et on choisit usuellement en orientant les angles du plan selon la « règle de la main droite » ou une autre équivalente vue au paragraphe « base directe d'un espace orienté à droite » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » on pourrait mais on ne le fera jamais choisir et utiliser la « règle de la main gauche concernant les bases indirectes » vue dans le même chapitre, cela donnerait la même orientation des angles du plan.
- ↑ Ou encore « rayon (polaire) » s'exprimant en .
- ↑ Ou « abscisse angulaire » ou encore « angle polaire » s'exprimant en , sa détermination principale pouvant encore être choisie sur .
- ↑ Ce qui signifie que , les angles du plan étant orientés par .
- ↑ Comme la base orthonormée cartésienne , la base orthonormée polaire permet d'exprimer tout vecteur du plan , à la différence que ces vecteurs de base polaire dépendent de l'abscisse angulaire du point alors que les vecteurs de base cartésienne sont constants.
- ↑ Le vecteur position dépend explicitement de et implicitement de par l'intermédiaire de .
- ↑ Les composantes cylindro-polaires de sont donc , à distinguer des coordonnées cylindro-polaires de qui sont la 2ème coordonnée cylindro-polaire étant angulaire ne peut être qualifiée d'« orthoradiale », qualificatif réservé aux grandeurs linéaires ou déduites de grandeurs linéaires.
- ↑ 12,0 12,1 12,2 12,3 et 12,4 On utilise les formules de trigonométrie suivantes et suivies éventuellement de l'utilisation de la parité de la fonction cosinus et de l'imparité de la fonction sinus .
- ↑ étant défini à près, il faut simultanément les expressions de et pour déterminer la valeur de .
- ↑ Ce demi-plan est parfaitement défini si .
- ↑ Angle orienté par le vecteur unitaire au plan selon la « règle de la main droite » ou une autre équivalente vue au paragraphe « base directe d'un espace orienté à droite » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » c'est le même vecteur unitaire que celui orientant l'angle du repérage cylindro-polaire, ce n'est pas surprenant puisqu'il s'agit en fait du même angle.
- ↑ Le vecteur unitaire au demi plan méridien et orientant la colatitude reste à préciser, son sens est régi par la « règle de la main droite » ou une autre équivalente vue au paragraphe « base directe d'un espace orienté à droite » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) »
- ↑ 17,0 et 17,1 Le qualificatif de pôle est mis entre parenthèses car le plus souvent omis.
- ↑ Ou encore « coordonnée radiale » s'exprimant en .
- ↑ Domaine de définition large de seulement car on décrit un demi-plan méridien.
- ↑ Domaine de définition large de , on peut choisir encore une détermination comprise entre et .
- ↑ Le plan est encore appelé « plan équatorial ».
- ↑ Ce qui signifie que , les angles du demi-plan méridien étant orientés par .
- ↑ Le sens de permet d'obtenir l'orientation de la colatitude du point considéré selon la « règle de la main droite » ou une autre équivalente vue au paragraphe « base directe d'un espace orienté à droite » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ 24,0 24,1 24,2 24,3 et 24,4 Ce 3ème vecteur de base sphérique est identique au 2ème vecteur de base cylindro-polaire.
- ↑ On pourrait encore l'appeler « vecteur colatitudinal » mais cela n'est pas fait pour des raisons de sonorité de la langue.
- ↑ Comme la base orthonormée cylindro-polaire , la base orthonormée sphérique permet d'exprimer tout vecteur du demi-plan méridien, en fonction de pour la 1ère et pour la 2nde, le demi-plan étant orienté par le même vecteur .
- ↑ On aurait pu encore l'appeler « vecteur longitudinal » plus harmonieux à l'oreille mais cela n'est pas fait car on accorde usuellement un autre sens à « longitudinal » celui complémentaire de « transversal ».
- ↑ Le vecteur position dépend explicitement de et implicitement de par l'intermédiaire de .
- ↑ Les composantes sphériques de sont donc , à distinguer des coordonnées sphériques de qui sont les 2ème et 3ème coordonnées sphériques étant angulaires ne peuvent être qualifiées d'« orthoradiale » ni de « longitudale », qualificatif réservé aux grandeurs linéaires ou déduite de grandeurs linéaires en ce qui concerne « orthoradial » et que l'on étendra à « longitudal ».
- ↑ En géographie on utilise préférentiellement la latitude notée pour repérer le point dans un demi-plan méridien à partir du point d'intersection de ce demi-plan avec le plan de l'équateur ; la latitude est orientée en sens inverse de la colatitude c.-à-d. comptée positivement du pôle Sud vers le pôle Nord, elle est définie selon , nulle quand est sur l'équateur, valant au pôle Nord et au pôle Sud ; son lien avec la colatitude est donnant effectivement une valeur nulle au pôle Nord, à l'équateur et au pôle Sud.
- ↑ 31,0 et 31,1 La 3ème cordonnée sphérique étant la même que la 2nde coordonnée cylindro-polaire .
- ↑ Ce n'est guère que dans le cadre de la cinématique quand on s'intéresse au vecteur accélération du point qu'on peut envisager de convertir le repérage sphérique en repérage cylindro-polaire car les expressions du vecteur accélération en repérage sphérique sont très compliquées alors qu'en repérage cylindro-polaire elles le sont nettement moins.
- ↑ On décompose d'abord les vecteurs de base sphérique dans la base cylindro-polaire puis ces derniers dans la base cartésienne
- ↑ On utilise d'abord le passage des coordonnées sphériques aux coordonnées cylindro-polaires avant de se servir du passage des coordonnées cylindriques aux coordonnées cartésiennes.
- ↑ , il faut simultanément les expressions de et pour déterminer la valeur de .
- ↑ On utilise d'abord le passage des coordonnées cartésiennes aux coordonnées cylindro-polaires avant de se servir du passage des coordonnées cylindriques aux coordonnées sphériques.
- ↑ Suivre une certaine direction c'est suivre une certaine droite, donc un cas particulier de suivre une courbe.
- ↑ Voir le paragraphe « définition intrinsèque du vecteur déplacement élémentaire le long d'une courbe continue » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ Il est rappelé que ce vecteur est unique à condition que ne soit pas un point anguleux de la courbe.
- ↑ On rappelle que, dans le cas général, le vecteur déplacement élémentaire le long d'une courbe continue n'est pas nul, ceci n'arrivant que très rarement.
- ↑ 41,0 et 41,1 On rappelle qu'une courbe dans l'espace à trois dimensions est caractérisée par deux équations cartésiennes, chaque équation cartésienne caractérisant une surface : étant l'équation du plan et l'équation d'un cylindre parabolique de génératrices à un cylindre étant généré par une droite « génératrice » ici de direction se déplaçant le long d'une courbe « directrice » ici la parabole le résultat étant encore appelé surface cylindrique.
- ↑ Il suffit de remplacer, dans l'expression générale du vecteur déplacement élémentaire, et par leur expression en fonction de .
- ↑ Si on essaie d'imaginer l'évolution du vecteur déplacement élémentaire on obtient mentalement l'allure du graphe de la parabole, le vecteur déplacement élémentaire étant tangent à la parabole.
- ↑ Le 1er vecteur de la base cylindro-polaire dépendant de sa différentielle n'est pas nulle contrairement au 3ème vecteur de cette base qui, étant constant, est de différentielle nulle.
- ↑ On écrit sous cette forme car il est directement à .
- ↑ 46,0 et 46,1 Voir le paragraphe « définition intrinsèque de la différentielle d'une fonction vectorielle d'une variable » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ Pour l'évaluation des dérivées, voir le paragraphe « définition de la dérivée et de la différentielle d'une fonction vectorielle par choix d'une base dans l'espace physique incluant l'espace image de la fonction vectorielle » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ En utilisant le fait que les dérivées des fonctions sinus ou cosinus par rapport à leur argument s'obtiennent en augmentant l'argument de .
- ↑ La longueur d'un arc de cercle de rayon correspondant à un angle au centre exprimé en étant , voir le paragraphe « exemples de longueur de courbe ou d'arc de courbe (à retenir) » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ 50,0 50,1 50,2 50,3 et 50,4 Elle est donc tracée sur un tuyau cylindrique de révolution avec si on « développe » le tuyau cylindrique de façon à ce que sa surface latérale devienne un plan, l'hélice devient une droite de pente égale au cœfficient de proportionnalité entre et ,
Modèle:Alelle est qualifiée de « dextre » ou « droite » si le cœfficient de proportionnalité entre et est positif, ce qui correspond au fait qu'elle « monte » dans le sens trigonométrique, un observateur placé à l’extérieur la voit, lorsqu'elle est devant, « monter de gauche à droite » ;
Modèle:Alelle serait qualifiée de « senestre » ou « gauche » si le cœfficient de proportionnalité entre et était négatif, elle « monterait » dans le sens trigonométrique indirect ou rétrograde ou encore dans le sens horaire. - ↑ 51,0 et 51,1 On rappelle qu'une courbe dans l'espace à trois dimensions est caractérisée par deux équations donc ici deux équations cylindro-polaires, chaque équation caractérisant une surface :
Modèle:Al étant l'équation d'un tuyau cylindrique de révolution d'axe et de rayon ,
Modèle:Al l'équation d'une surface hors nomenclature mais que l'on pourrait appelée « rampe en colimaçon » elle est constituée de demi-droites à , dans la direction repérée par et issues du point de l'axe de côte c.-à-d. de valeur absolue d'autant plus grande que l'est, voir tracé à droite de celui de l'hélice circulaire. - ↑ Ne pas oublier le déplacement suivant .
- ↑ L'hélice circulaire est alors qualifiée de « gauche ».
- ↑ L'hélice circulaire est alors qualifiée de « droite ».
- ↑ Si on essaie d'imaginer l'évolution du vecteur déplacement élémentaire on obtient mentalement l'allure du graphe de l'hélice circulaire, le vecteur déplacement élémentaire étant tangent à l'hélice.
- ↑ Pour l'hélice circulaire droite étudiée, la pente de la droite correspondant au « développement » de l'hélice circulaire est de pente où est la longueur de l'arc de cercle de la base du tuyau cylindrique de révolution correspondant à la variation ou encore de pente .
- ↑ Ou le sens direct ou encore le sens antihoraire ou, mais très peu utilisé, le sens prograde.
- ↑ Ou le sens indirect ou encore le sens horaire ou, assez fréquemment utilisé, le sens rétrograde.
- ↑ Le 1er vecteur de la base sphérique dépendant de et sa différentielle n'est pas nulle son évaluation étant moins aisée que celle des deux 1ers vecteurs de base cylindro-polaire, nous ne la verrons qu'en complément.
- ↑ En repérage géographique le déplacement serait suivant la verticale dans le sens ascendant.
- ↑ En repérage géographique le déplacement serait suivant l'horizontale dirigée vers le Sud.
- ↑ Le rayon du demi-cercle méridien étant et la longueur d'un arc de cercle de rayon d'angle au centre associé exprimé en étant , voir le paragraphe « exemples de longueur de courbe ou d'arc de courbe (à retenir) » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ En repérage géographique le déplacement serait suivant l'horizontale dirigée vers l'Est.
- ↑ Le rayon du cercle « parallèle » étant voir schéma de profil dans le demi-plan méridien , le rayon y étant et la longueur d'un arc de cercle de rayon correspondant à un angle au centre exprimé en étant , voir le paragraphe « exemples de longueur de courbe ou d'arc de courbe (à retenir) » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ Voir, pour les deux 1ères différentielles, le paragraphe « écriture de la différentielle du champ (ou de la fonction) vectoriel(le) de l'espace, une base cartésienne de ce dernier ayant été choisie » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » mais ici, les dérivées partielles seront définies à l'aide des coordonnées sphériques et non cartésiennes ;
Modèle:Alvoir, pour la 3ème différentielle, le paragraphe « définition de la dérivée et de la différentielle d'une fonction vectorielle par choix d'une base dans l'espace physique incluant l'espace image de la fonction vectorielle » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ». - ↑ 66,0 et 66,1 On fait une permutation circulaire pour que le 2ème vecteur de la base cylindro-polaire devienne le 3ème vecteur comme il l'est dans la base sphérique.
- ↑ 67,0 et 67,1 On rappelle que est figé pendant la durée de la dérivation c.-à-d. que ne varie pas.
- ↑ 68,0 et 68,1 On rappelle que est figé pendant la durée de la dérivation.
- ↑ 69,0 69,1 69,2 et 69,3 On rappelle la propriété établie dans le paragraphe « différentielle des vecteurs de base cylindro-polaire (à retenir) » plus haut dans ce chapitre et qui reste applicable ici : « quand on dérive un vecteur unitaire d'un plan fixe par rapport à l'angle qu'il fait avec une direction fixe de ce plan, on obtient un vecteur unitaire de ce plan directement au vecteur initial », ainsi
Modèle:Aldérivant par rapport à l'angle qu'il fait avec , le plan équatorial les contenant tous deux étant fixe on obtient se déduisant de par rotation de dans le plan équatorial ;
Modèle:Aldérivant par rapport à l'angle qu'il fait avec , le plan équatorial les contenant tous deux étant fixe on obtient se déduisant de par rotation de dans le plan équatorial.
Modèle:AlDérivant par rapport à l'angle qu'il fait avec , le plan de la courbe les contenant tous deux étant fixe on obtient se déduisant de par rotation de dans le plan de la courbe. - ↑ étant un vecteur unitaire du demi-plan méridien, on n'utilise que la partie de base sphérique située dans ce demi-plan à savoir .
- ↑ Il est rappelé que seule sa détermination géométrique est une exigence.
- ↑ 72,0 et 72,1 Louis Poinsot (1777 - 1859) mathématicien français surtout connu pour ses travaux en mécanique rationnelle et aussi quelques travaux de géométrie.
- ↑ 73,0 et 73,1 Une loxodromie de sphère est une courbe tracée sur une sphère telle qu'elle coupe les parallèles de cette sphère à angle constant, l'angle valant ici ; comme toute courbe de l'espace elle est déterminée par deux équations, dans le cas présent deux équations sphériques dont la 1ère est l'équation de la sphère de centre et de rayon et la 2ème l'équation d'une surface hors nomenclature constituée de demi-droites issues de caractérisées par sa colatitude et sa longitude associée
Modèle:AlUsuellement la 2ème équation est donnée en fonction de la latitude soit ou, avec , la réécriture de l'équation selon . - ↑ Voir le paragraphe « différenteille d'une fonction scalaire d'une variable » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ Dérivation de fonctions composées : on dérive le logarithme népérien par rapport à son argument d'où , on multiplie par la dérivée de l'argument par rapport à l'argument de ce dernier soit et on termine en multipliant par la dérivée de par rapport à soit
- ↑ On utilise la formule de trigonométrie .
- ↑ Le vecteur déplacement élémentaire suivant étant .
- ↑ On pourrait s'étonner des signes obtenus mais il ne faut pas oublier que variant de à , est , ainsi
Modèle:Alle vecteur déplacement élémentaire selon un demi-cercle méridien est bien en sens contraire de et
Modèle:Alcelui selon un parallèle dans le sens de . - ↑ La norme du vecteur déplacement élémentaire étant égale à d'après soit finalement «» en utilisant établissant que « est effectivement indépendant de » ;
Modèle:Alle plan tangent à la sphère au point étant de vecteurs de base , la pente calculée par rapport aux parallèles et comptée positivement vers le Nord est c.-à-d. « une pente effectivement indépendante de » la direction de faisant un angle constant de par rapport aux parallèles. - ↑ 80,0 80,1 et 80,2 Le tracé a été fait avec «» ; la courbe est en rouge.
- ↑ Pour en déduire deux équations non paramétriques cartésiennes, cylindro-polaires ou sphériques nécessaires à la caractérisation de la courbe, il suffit d'éliminer le paramètre entre ces trois équations paramétriques cartésiennes, cylindro-polaires ou sphériques ;
Modèle:Alles deux équations non paramétriques obtenues ne sont pas uniques, en effet si on nomme les équations paramétriques de la courbe, on peut éliminer le paramètre- entre et , entre et d'où un 1er couple d'équations non paramétriques possibles ou
- entre et , entre et d'où un 2ème couple d'équations non paramétriques possibles ou encore
- entre et , entre et d'où un 3ème couple d'équations non paramétriques possibles.
- ↑ La façon de procéder serait la même en repérage paramétrique cylindro-polaire ou en repérage paramétrique sphérique.
- ↑ On aurait pu éliminer le paramètre à l'aide de la 3ème équation paramétrique selon «» donnant par report «» c.-à-d. l'équation cartésienne d'un plan à il s'agit du même plan que celui trouvé en éliminant le paramètre à l'aide de la 1ère équation paramétrique.
- ↑ On aurait pu éliminer le paramètre à l'aide de la 3ème équation paramétrique selon «» donnant par report «» c.-à-d. l'équation cartésienne d'un cylindre parabolique de génératrices à .
- ↑ En utilisant les notes « 85 » et « 86 » exposées plus haut dans ce chapitre consistant à éliminer à l'aide de l'équation paramétrique on a trouvé pour les deux équations cartésiennes de «» étant l'intersection d'un cylindre parabolique de génératrices à et d'un plan à est effectivement une parabole bien qu'il s'agisse ici d'un cylindre parabolique distinct de celui intervenant dans le corps du paragraphe, la parabole est évidemment la même.
- ↑ Souvent encore noté , ce qui ne pose aucun problème si le repérage sphérique n'est pas simultanément utilisé.
- ↑ C.-à-d. hors mécanique ondulatoire domaine dans lequel les particules sont considérées comme des ondes de probabilité de présence réparties dans l'espace et non comme des objets y étant parfaitement localisés, les endroits de maximum de probabilité de présence s'identifiant à ce que seraient les trajectoires des particules si elles étaient considérées comme des objets localisés dans l'espace.
- ↑ Dans le cadre de la mécanique classique, l'électron est une particule quasi-ponctuelle et le noyau aussi, le mouvement ainsi étudié aboutit à certains résultats non observés expérimentalement, le physicien Niels Bohr a ajouté une condition que le mouvement de l'électron devait suivre pour être en accord avec l'expérience, cette condition porte sur le « moment cinétique » de l'électron Modèle:Nobr caractérisant la rotation orbitale de l'électron, cette grandeur étant introduite dans le paragraphe « définition du vecteur moment cinétique du point matériel M dans le référentiel d'étude par rapport à un point A » du chap. de la leçon « Mécanique 2 (PCSI) » qui, selon Niels Bohr, devait être un multiple d'une grandeur connue sous le nom de constante réduite de Planck , étant la constante de Planck ; le problème du mouvement de l'électron particule ponctuelle dans l'atome d'hydrogène avec cette condition de quantification est connu sous le nom de « modèle de Bohr de l'atome d'hydrogène » ce qui est extraordinaire c'est que l'on trouve ainsi les bons résultats expérimentaux bien que la condition de quantification du moment cinétique de l'électron se soit révélée par la suite fausse en effet dans le cadre de la mécanique ondulatoire on peut aussi définir un moment cinétique pour l'onde électronique mais le nombre quantique intervenant n'est pas celui considéré dans le modèle de Bohr de l'atome d'hydrogène, étonnant non ! ;
Modèle:AlNiels Henrik David Bohr (1885 - 1962), physicien danois, surtout connu pour son apport à la construction de la mécanique quantique, a obtenu le prix Nobel de physique en « pour ses contributions à la recherche sur la structure des atomes et sur le rayonnement qu'ils émettent » ;
Modèle:AlMax Karl Ernst Ludwig Planck (1858 - 1947), physicien allemand, l'un des fondateurs de la mécanique quantique, a obtenu le prix Nobel de physique en « pour ses travaux en théorie des quanta » ; en son hommage, la période de l'histoire cosmologique suivant immédiatement l'apparition de l'Univers pendant laquelle les quatre interactions fondamentales électromagnétisme, interaction faible, interaction forte et gravitation n'en formait qu'une, fut baptisée « ère de Planck », sa durée « temps de Planck » étant estimée à . - ↑ Toutefois le vecteur-accélération d'un point dans le système de coordonnées sphériques étant trop compliqué pour être retenu ou trop long à établir pour être retrouvé, on se ramènera au système de coordonnées le plus proche pour appliquer la r.f.d.n. relation fondamentale de la dynamique newtonienne à savoir le repérage cylindro-polaire
- ↑ 90,00 90,01 90,02 90,03 90,04 90,05 90,06 90,07 90,08 90,09 90,10 90,11 et 90,12 Jean Frédéric Frenet (1816 - 1900) est un mathématicien, astronome et météorologue français à qui on doit six des neuf formules de géométrie différentielle associées au trièdre (ou base) de Serret-Frenet Joseph-Alfred Serret (1819 - 1885) mathématicien et astronome français ayant trouvé indépendamment ces formules.
- ↑ Il n'est donc pas exigible pour un étudiant de classe préparatoire option PCSI.
- ↑ Traduisant le fait que la vitesse lue sur le tachymètre augmente ou diminue.
- ↑ La distance non algébrisée séparant de sur étant .
- ↑ 94,0 94,1 94,2 94,3 94,4 94,5 et 94,6 En un point anguleux d'une courbe continue on définit deux tangentes ne coïncidant pas, l'une à gauche et l'autre à droite, pour un point non anguleux il n'existe donc qu'une seule tangente.
- ↑ 95,0 et 95,1 Une définition plus précise également valable pour une courbe gauche pourrait être : soient un point de et un point voisin de sur , le cercle osculateur Modèle:Nobr appelé cercle de courbure de la courbe au point est la limite du cercle passant par et en étant tangent à en quand tend vers , voir aussi le paragraphe « Définitions et propriétés » de l'article de « wikipédia » intitulé « cercle osculateur ».
- ↑ Pour définir un cercle osculateur il faut qu'il existe une tangente unique au point , on ne peut donc pas définir un cercle osculateur en un point anguleux où existe une tangente à gauche de la tangente à droite mais on peut définir un cercle osculateur à gauche et un cercle osculateur à droite.
- ↑ Comme , un rayon de courbure est une grandeur positive ou nulle.
- ↑ Pour définir un plan osculateur il faut bien sûr que les plans tangents existent c.-à-d. qu'il existe une tangente unique au point , tout plan contenant cette tangente et il y en a une infinité définissant alors un plan tangent particulier, parmi tous ces plans il en existe un se rapprochant localement le plus de la courbe c'est le plan osculateur.
- ↑ La notion de plan osculateur a été introduite par Alexis Claude Clairaut (1713 - 1765) mathématicien français particulièrement précoce à l'âge de douze ans il écrit un mémoire sur quatre courbes géométriques et entre à l'Académie des Sciences à dix-huit ans, on lui doit des travaux en analyse mathématique, en géométrie différentielle et en géodésie science s'attachant à résoudre les dimensions et la forme de la Terre.
- ↑ La normale principale à en est encore la direction normale dans le plan osculateur ou le plan de la courbe si cette dernière est plane.
- ↑ Ou, si la courbe est plane, au plan de la courbe ; ce plan étant usuellement noté et le vecteur normal secondaire est noté ou suivant le sens du vecteur normal secondaire défini ci-après.
- ↑ Ainsi l'angle entre le vecteur unitaire tangentiel et le vecteur normal principal est .
Modèle:AlSi la courbe est plane dans le plan , le sens «» des mesures d'angle de ce plan doit être tel que ;
Modèle:Transparentor ce sens «» est déterminé par le sens du vecteur normal secondaire, d'où
Modèle:AlModèle:Transparentle vecteur normal secondaire est si correspondant à directe, le plan étant orienté dans le sens
Modèle:AlModèle:Transparenttrigonométrique ou anti-horaire ou
Modèle:AlModèle:Transparentle vecteur normal secondaire est si correspondant à indirecte, le plan étant orienté
Modèle:AlModèle:Transparentdans le sens anti-trigonométrique ou horaire.
Modèle:AlRemarque : voir les notes « 58 » et « 59 » plus haut dans ce chapitre pour d'autres appellations synonymes de trigonométrique et anti-trigonométrique. - ↑ Ce pourrait être un point fixe de et en particulier le point .
- ↑ 104,0 104,1 104,2 104,3 et 104,4 Voir le paragraphe « rappel, notion d'abscisse curviligne d'un point et vecteur unitaire tangentiel, 1er vecteur de la base locale de Frenet associée » plus haut dans ce chapitre.
- ↑ 105,0 et 105,1 Omis pour une courbe plane d'où les parenthèses.
- ↑ 106,0 et 106,1 Voir le paragraphe « 2ème vecteur de la base de Frenet associée à un point de la courbe : vecteur unitaire normal principal » plus haut dans ce chapitre.
Modèle:AlLe vecteur unitaire normal principal de Frenet en un point non anguleux d'une courbe plane est directement au vecteur unitaire tangentiel en de « directement » car on choisit d'orienter le plan de la courbe tel que l'angle algébrisé , le vecteur unitaire normal secondaire au plan de la courbe orientant ces angles étant, dans le cas de la figure, de sens opposé à mais il serait dans le sens de si la courbure de en était inversée, c.-à-d. si le centre de courbure associé était de l'autre côté de voir aussi la note « 104 » plus haut dans ce chapitre. - ↑ Par égalité d'angles à côtés respectivement , cette propriété étant applicable à condition qu'il n'y ait pas de point d'inflexion de entre et , en effet la présence d'un point d'inflexion de entre et une inversion de courbure de entre ces deux points et comme le vecteur unitaire normal est toujours de sens vers le centre de courbure associé, un positionnement inverse de par rapport à entre les deux points ce qui nécessite que les sens de mesure des angles soient inversés lors du passage d'un point à l'autre d'où l'inapplicabilité de la propriété énoncée.
- ↑ d'un point d'inflexion de .
- ↑ À chaque valeur d'abscisse curviligne on associe un point que la courbe soit ouverte ou fermée et à chaque point , non anguleux, on associe une valeur de , aussi peut-on définir de façon unique la fonction ; en restreignant éventuellement le domaine de définition de on peut alors inverser la fonction pour obtenir la fonction inverse ; dans «» on reconnaît la définition de la dérivée par rapport à de .
- ↑ L'établissement de cette formule a nécessité que ne soit pas un point d'inflexion de mais
Modèle:Aldans le cas où serait un point d'inflexion de , le rayon de courbure y étant infini et y étant stationnaire infini d'où l'applicabilité de la formule en un point d'inflexion de . - ↑ 111,0 et 111,1 Cette définition ou relation ne s'applique qu'à une courbe plane.
- ↑ 112,0 et 112,1 Voir le paragraphe « définition du rayon de courbure en un point non anguleux d'une courbe plane » plus haut dans ce chapitre.
- ↑ 113,0 et 113,1 La courbure étant l'inverse du rayon de courbure et s'exprimant en .
- ↑ On vérifie l'homogénéité «» est en et «» en , «» et «» étant sans dimension.
- ↑ Voir le paragraphe « établissement de la définition simultanée du 2ème vecteur de la base locale de frenet et du rayon de courbure en un point non anguleux d'une courbe plane » plus haut dans ce chapitre.
- ↑ 116,0 116,1 et 116,2 Voir le paragraphe « 2ème vecteur de la base de Frenet associée à un point de la courbe : vecteur unitaire normal principal » plus haut dans ce chapitre.
- ↑ 117,0 117,1 et 117,2 Voir le paragraphe « notion de plan et cercle osculateurs en un point d'une courbe gauche, centre et rayon de courbure en ce point » plus haut dans ce chapitre.
- ↑ Les définitions et expressions ayant permis d'établir cette relation pour une courbe plane n'ayant aucune signification pour une courbe gauche, seule cette relation est utilisable dans le cas d'une courbe gauche.
- ↑ Obtenue en dérivant l'équation paramétrique vectorielle de la courbe par rapport à .
- ↑ Voir le paragraphe « 3ème vecteur de la base de Frenet associée à un point de la courbe : vecteur unitaire normal secondaire » plus haut dans ce chapitre.