Mécanique 2 (PCSI)/Loi du moment cinétique : Moments cinétiques d'un point matériel

La notion de moment cinétique n'est au programme de physique de P.C.S.I. que dans son aspect newtonien.

Aspect de la cinétique du point matériel M dans le référentiel d'étude relativement à un autre point A : définition dans le référentiel d’étude du « moment cinétique de M par rapport au point A » (ou « moment cinétique vectoriel de M »)

Introduction

Modèle:AlIl s'agit d’une part, de décrire le mouvement du point matériel $M$ dans le référentiel d'étude $ℛ$ relativement à un point privilégié $A$ et
Modèle:AlModèle:Transparentd'autre part, de tenir compte de l'inertie du point matériel $M$ $($c'est-à-dire de sa masse$)$.

Définition du vecteur « moment cinétique du point matériel M dans le référentiel d’étude par rapport à un point A »

Schéma de définition du moment cinétique $($vectoriel$)$ d'un point matériel $M$ par rapport à un point $A$ dans le référentiel d'étude orienté à droite

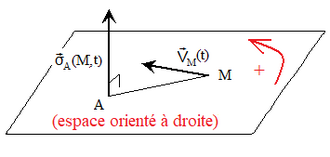
Modèle:AlCommentaires : cette grandeur traduit la réserve de « mouvement inertiel » du point matériel $M$ par rapport au point $A$, elle tient compte de l'inertie d'une part et de la vitesse en norme, direction et sens d'autre part, le tout relativement au point $A$, la grandeur dépend donc du référentiel $(ℛ)$ ;

Modèle:AlModèle:Transparentle point $A$ est le point par rapport auquel on calcule le moment cinétique $($vectoriel$)$ $[$encore appelé point origine de calcul$]$, le moment cinétique $($vectoriel$)$ «${\overrightarrow{\sigma }}_A(M,t)$» est représenté au point $A$ $($voir ci-contre dans le cas d'un espace orienté à droite$)$ ;

Modèle:AlModèle:Transparentle moment cinétique du point matériel $M$ par rapport à $A$ est un vecteur axial $($ou pseudo-vecteur$)$ comme produit vectoriel de deux vecteurs polaires $($ou vrais vecteurs$)$ $[$voir le paragraphe « propriété du produit vectoriel de deux vrais vecteurs, de deux pseudo-vecteurs ou d'un vrai vecteur et d'un pseudo-vecteur » du chap.$20$ de la leçon « Outils mathématiques pour la physique (PCSI) »$]$, son sens dépend donc de l'orientation de l'espace $[$si l'espace est orienté à gauche $($ce qui est excessivement rare$)$ le sens de ${\overrightarrow{\sigma }}_A(M,t)$ est inversé par rapport à celui représenté sur le schéma ci-contre$]$.

Modèle:AlRemarque : avec la notion $($hors programme de physique de P.C.S.I.$)$ de « torseur » introduite dans le chap.$1$ de la leçon « Outils mathématiques pour la physique - bis (PCSI) », on remarque que le moment cinétique $($vectoriel$)$ du point matériel $M$ par rapport à $A$ c'est-à-dire ${\overrightarrow{\sigma }}_A(M,t)$ est le moment du torseur cinétique du point matériel $M$ à savoir ${𝒯}_{\text{cinét. de}M}$ dont les éléments de réduction sont évalués en $A$ soit ${𝒯}_{\text{cinét. de}M}=$ ${\left\{\begin{array}{c}{\overrightarrow{p}}_M(t)=m{\overrightarrow{V}}_M(t)\\ {\overrightarrow{\sigma }}_A(M,t)=\overrightarrow{AM}(t)\wedge {\overrightarrow{p}}_M(t)\end{array}\right\}}_A$.

Propriétés du « moment cinétique (vectoriel) de M dans le référentiel d’étude par rapport au point origine A »

Modèle:AlLes propriétés du « moment cinétique $($vectoriel$)$ du point matériel $M$ dans le référentiel d’étude $ℛ$ par rapport au point origine $A$» ${\overrightarrow{\sigma }}_A(M,t)=$ $\overrightarrow{AM}(t)\wedge {\overrightarrow{p}}_M(t)$ se déduisent de la définition d’un produit vectoriel à savoir :

• produit vectoriel $\left\{\begin{array}{c}=\overrightarrow{0}\text{si}A\in \text{au support de}{\overrightarrow{p}}_M(t)\\ \ne \overrightarrow{0}\text{sinon }\left(\text{voir figure ci-dessus}\right)\end{array}\right\}$ et
• dans le cas où ${\overrightarrow{\sigma }}_A(M,t)\ne \overrightarrow{0}$, les direction, sens et norme sont
  Modèle:Al$\succ$direction $\perp$ au plan $\{A,{\overrightarrow{p}}_M(t)\}$,
  Modèle:Al$\succ$sens tel que le trièdre $\{\overrightarrow{AM}(t),{\overrightarrow{p}}_M(t),{\overrightarrow{\sigma }}_A(M,t)\}$ soit direct dans le cas présent où l'espace est orienté à droite et
  Modèle:Al$\succ$norme $\Vert {\overrightarrow{\sigma }}_A(M,t)\Vert =\Vert \overrightarrow{AM}(t)\Vert \Vert {\overrightarrow{p}}_M(t)\Vert |\sin \left\{\widehat{[\overrightarrow{AM}(t),{\overrightarrow{p}}_M(t)]}\right\}|$ en $kg\cdot m^2\cdot s^{-1}$ ;

Modèle:Alremarque : si le mouvement de $M$ est plan et si $A$ est choisi dans le plan de la trajectoire de $M$, ${\overrightarrow{\sigma }}_A(M,t)$ est $\perp$ au plan $($dans la mesure où il n’est pas nul$)$ et « son Modèle:Nobr précise le sens de « rotation » relativement à $A$ dans le plan.

« Vecteur moment cinétique de M par rapport au point origine A », cas particulier de « vecteur moment d’un champ vectoriel défini en M par rapport au point origine A »

Modèle:AlDe façon générale, le « vecteur moment d’un champ vectoriel $\overrightarrow{C}(M)$Modèle:, par rapport à $A$ $($point origine de calcul du moment$)$» étant défini selon $\overrightarrow{AM}\wedge \overrightarrow{C}(M)$, on en déduit que
Modèle:AlModèle:Transparentle « vecteur moment cinétique du point matériel $M$ dans le référentiel $ℛ$ par rapport à $A$ $($point origine de calcul du moment cinétique$)$» est le « vecteur moment de la quantité de mouvement ${\overrightarrow{p}}_M$ du point matériel $M$ dans le référentiel $ℛ$ par rapport à $A$ $($point origine de calcul du moment$)$».

Complément, expression « relativiste » du « vecteur moment cinétique de M dans le référentiel d’étude par rapport au point origine A »

Modèle:AlLa notion de « vecteur moment d’un champ vectoriel

$\overrightarrow{C}(M)$

Modèle:, par rapport à un point origine

$A$

» étant

$\overrightarrow{AM}\wedge \overrightarrow{C}(M)$

et ceci indépendamment de toute cinétique,
Modèle:Alle « vecteur moment cinétique du point matériel

$M$

par rapport au point origine

$A$

dans un référentiel

$ℛ$

»

${\overrightarrow{\sigma }}_A(M,t)$

est défini comme le « vecteur moment de la quantité de mouvement

${\overrightarrow{p}}_M$

du point matériel

$M$

par rapport au point origine

$A$

», que le mouvement de

$M$

dans

$ℛ$

soit classique ou relativiste soit,

« en cinétique relativiste, ${\overrightarrow{\sigma }}_A(M,t)=\overrightarrow{AM}(t)\wedge {\overrightarrow{p}}_M(t)$» ;

Modèle:All'expression relativiste, dans le référentiel $ℛ$, de la quantité de mouvement ${\overrightarrow{p}}_M$ du point matériel $M$ en fonction de sa masse $m$ et de sa vitesse ${\overrightarrow{V}}_M(t)$ dans $ℛ$, a été introduite dans le paragraphe « définition du (vecteur) quantité de mouvement du point matériel dans le cadre de la cinétique relativiste » du chap.$7$ de la leçon « Mécanique 1 (PCSI) »,

• elle nécessite de définir le « facteur de Lorentz du point $M$ dans le référentiel $ℛ$ par ${\gamma }_M(t)=\frac{1}{\sqrt{1-{\left[\frac{\Vert {\overrightarrow{V}}_M(t)\Vert }{c}\right]}^2}}$» et
• la quantité de mouvement de $M$ dans $ℛ$ s'écrit alors «${\overrightarrow{p}}_M(t)={\gamma }_M(t)m{\overrightarrow{V}}_M(t)$» ou encore,
  «${\overrightarrow{p}}_M(t)=m_{\text{app}}(t){\overrightarrow{V}}_M(t)$» en définissant la « masse apparente de $M$ dans $ℛ$ par
  $m_{\text{app}}(t)={\gamma }_M(t)m=\frac{m}{\sqrt{1-{\left[\frac{\Vert {\overrightarrow{V}}_M(t)\Vert }{c}\right]}^2}}$» ;

Modèle:Alpar cette expression on en déduit l'expression relativiste, dans

$ℛ$

, du vecteur moment cinétique du point matériel

$M$

par rapport au point origine

$A$

en fonction, entre autres, de la vitesse de

$M$

dans

$ℛ$ «${\overrightarrow{\sigma }}_{A,\text{relativ}}(M,t)=\overrightarrow{AM}(t)\wedge {\gamma }_M(t)m{\overrightarrow{V}}_M(t)$»
avec «${\gamma }_M(t)=\frac{1}{\sqrt{1-{\left[\frac{\Vert {\overrightarrow{V}}_M(t)\Vert }{c}\right]}^2}}$ le facteur de Lorentz de $M$ dans $ℛ$»
soit encore,
«${\overrightarrow{\sigma }}_{A,\text{relativ}}(M,t)={\gamma }_M(t){\overrightarrow{\sigma }}_{A,\text{newton}}(M,t)$» où «${\overrightarrow{\sigma }}_{A,\text{newton}}(M,t)=\overrightarrow{AM}(t)\wedge m{\overrightarrow{V}}_M(t)$ est
l'expression classique du vecteur moment cinétique de $M$ par rapport à $A$ dans $ℛ$».

Modèle:AlRemarques : Conformément à ce qui est introduit dans le paragraphe « torseur cinétique » du chap.$1$ de la leçon « Outils mathématiques pour la physique - bis (PCSI) », les éléments de réduction du torseur cinétique du point matériel $M$ dans le référentiel $ℛ$ au point de réduction $A$ sont définis selon ${𝒯}_{\text{cinét. de }M}(t)={\left\{\begin{array}{c}{\overrightarrow{p}}_M(t)\\ {\overrightarrow{\sigma }}_A(M,t)=\overrightarrow{AM}(t)\wedge {\overrightarrow{p}}_M(t)\end{array}\right\}}_A$, expression applicable en cinétique classique ou relativiste et
Modèle:AlModèle:Transparentsuivant le caractère classique ou relativiste du mouvement du point matériel $M$ dans le référentiel $ℛ$ :
Modèle:AlModèle:Transparent$\succ$en cinétique classique ${𝒯}_{\text{cinét. newton. de }M}(t)={\left\{\begin{array}{c}{\overrightarrow{p}}_M(t)=m{\overrightarrow{V}}_M(t)\\ {\overrightarrow{\sigma }}_A(M,t)=\overrightarrow{AM}(t)\wedge m{\overrightarrow{V}}_M(t)\end{array}\right\}}_A$,
Modèle:AlModèle:Transparent$\succ$en cinétique relativiste ${𝒯}_{\text{cinét. relativ. de }M}(t)={\left\{\begin{array}{c}{\overrightarrow{p}}_M(t)={\gamma }_M(t)m{\overrightarrow{V}}_M(t)\\ {\overrightarrow{\sigma }}_A(M,t)=\overrightarrow{AM}(t)\wedge {\gamma }_M(t)m{\overrightarrow{V}}_M(t)\end{array}\right\}}_A={\gamma }_M(t){\left\{\begin{array}{c}{\overrightarrow{p}}_M(t)=m{\overrightarrow{V}}_M(t)\\ {\overrightarrow{\sigma }}_A(M,t)=\overrightarrow{AM}(t)\wedge m{\overrightarrow{V}}_M(t)\end{array}\right\}}_A={\gamma }_M(t){𝒯}_{\text{cinét. newton. de }M}(t)$ établissant l'importance de «${\gamma }_M(t)=$ $\frac{1}{\sqrt{1-{\left[\frac{\Vert {\overrightarrow{V}}_M(t)\Vert }{c}\right]}^2}}$» facteur de Lorentz du point matériel $M$ dans le référentiel $ℛ$ aussi bien dans la cinétique utilisant la résultante que dans celle utilisant le moment vectoriel en $A$ ;

Modèle:AlModèle:Transparenton remarque aussi que « les éléments de réduction du torseur cinétique relativiste du point matériel $M$ dans le référentiel $ℛ$ au point de réduction $A$ se déduisent de ceux du torseur cinétique classique du point matériel $M$ dans le même référentiel $ℛ$ au même point de réduction $A$» en y « substituant la masse $m$ du point matériel $M$ par la masse apparente de ce dernier à l'instant $t$, $m_{\text{app}}(t)$ $={\gamma }_M(t)m=\frac{m}{\sqrt{1-{\left[\frac{\Vert {\overrightarrow{V}}_M(t)\Vert }{c}\right]}^2}}$» soit «${𝒯}_{\text{cinét. relativ. de }M}(t)={\left\{\begin{array}{c}{\overrightarrow{p}}_M(t)=m_{\text{app}}(t){\overrightarrow{V}}_M(t)\\ {\overrightarrow{\sigma }}_A(M,t)=\overrightarrow{AM}(t)\wedge m_{\text{app}}(t){\overrightarrow{V}}_M(t)\end{array}\right\}}_A$».

Formule de changement d’origine du calcul des moments (cinétiques) vectoriels

Formule de changement d’origine du calcul de vecteur moment d’un champ vectoriel

Modèle:AlCette formule a été introduite dans le paragraphe « notion de résultante d'un torseur » du chap.

$1$

de la leçon « Outils mathématiques pour la physique - bis (PCSI) » sous le nom de « relation de Varignon Modèle:Nobr règle de transport des moments

$)$

», un champ de moments étant effectivement un torseur en tant que champ de vecteurs équiprojectif, elle s'écrit selon

«$\mathrm{\forall }(O,O^{\prime })\in {ℰ}^2,{\overrightarrow{ℳ}}_{O^{\prime }}[\overrightarrow{C}(M)]={\overrightarrow{ℳ}}_O[\overrightarrow{C}(M)]+\overrightarrow{O^{\prime }O}\wedge \overrightarrow{C}(M)$»Modèle:, ;

Modèle:Alici la démonstration s'effectue simplement en partant de la définition du vecteur moment du champ $\overrightarrow{C}(M)$ par rapport au point origine $O^{\prime }$ soit «${\overrightarrow{ℳ}}_{O^{\prime }}[\overrightarrow{C}(M)]$ $=\overrightarrow{O^{\prime }M}\wedge \overrightarrow{C}(M)$»,
Modèle:AlModèle:Transparenten utilisant la relation de Chasles «$\overrightarrow{O^{\prime }M}=\overrightarrow{O^{\prime }O}+\overrightarrow{OM}$» puis
Modèle:AlModèle:Transparentla distributivité de la multiplication vectorielle relativement à l'addition vectorielle soit «${\overrightarrow{ℳ}}_{O^{\prime }}[\overrightarrow{C}(M)]=\overrightarrow{O^{\prime }O}\wedge \overrightarrow{C}(M)+\overrightarrow{OM}\wedge \overrightarrow{C}(M)$», expression dans laquelle « le 2^nd terme du 2^ème membre étant ${\overrightarrow{ℳ}}_O[\overrightarrow{C}(M)]$ par définition », nous permet de conclure la démonstration.

Formule de changement d’origine du calcul du vecteur moment cinétique d’un point matériel dans le référentiel d’étude

Modèle:AlLe « vecteur moment cinétique du point matériel

$M$

dans le référentiel

$ℛ$

par rapport à

$A$ $($

point origine de calcul du moment cinétique

$)$

» étant le « vecteur moment de la quantité de mouvement

${\overrightarrow{p}}_M$

du point matériel

$M$

dans le référentiel

$ℛ$

par rapport à

$A$ $($

point origine de calcul du moment

$)$

», on peut lui appliquer la formule de changement d'origine du calcul du vecteur moment d'un champ vectoriel et on obtient

«$\mathrm{\forall }(O,O^{\prime })\in {ℰ}^2,{\overrightarrow{\sigma }}_{O^{\prime }}(M,t)={\overrightarrow{\sigma }}_O(M,t)+\overrightarrow{O^{\prime }O}\wedge {\overrightarrow{p}}_M(t)$»
applicable sous cette forme en cinétique classique ou relativiste.

Cas où M décrit un mouvement circulaire d’axe Δ, de rayon R et de vecteur rotation instantanée fixé

Schéma descriptif du mouvement d'un point matériel $M$ décrivant un cercle de centre $C$, de vecteur rotation instantanée $\overrightarrow{\mathrm{\Omega }}(t)$ imposé, avec précision du vecteur moment cinétique ${\overrightarrow{\sigma }}_C(M,t)$ de $M$ au point $C$ $($origine de calcul de moment cinétique$)$

Évaluation du vecteur moment cinétique de M en mouvement circulaire dans le référentiel d’étude par rapport au centre C du cercle

Modèle:AlConsidérant un point matériel

$M$

, de masse

$m$

, en mouvement circulaire de centre

$C$

, de vecteur rotation instantanée

$\overrightarrow{\mathrm{\Omega }}(t)$

dans le référentiel d'étude

$ℛ$

orienté à droite, le vecteur moment cinétique de ce point matériel

$M$

dans

$ℛ$

par rapport au centre

$C$

de sa trajectoire circulaire, noté

${\overrightarrow{\sigma }}_C(M,t)$

est défini par

«${\overrightarrow{\sigma }}_C(M,t)=\overrightarrow{CM}(t)\wedge {\overrightarrow{p}}_M(t)$» ou,
dans le cadre de la cinétique classique, «${\overrightarrow{\sigma }}_C(M,t)=\overrightarrow{CM}(t)\wedge m{\overrightarrow{V}}_M(t)$» ;

Modèle:Alinjectant dans cette dernière expression de

${\overrightarrow{\sigma }}_C(M,t)$

du cadre de la cinétique classique, l'expression intrinsèque du vecteur vitesse d'un point en mouvement circulaire de centre

$C$

et de vecteur rotation instantanée

$\overrightarrow{\mathrm{\Omega }}(t)$

, à savoir «

${\overrightarrow{V}}_M(t)=$ $\overrightarrow{\mathrm{\Omega }}(t)\wedge \overrightarrow{CM}(t)$

», on obtient Modèle:Nobr

$\overrightarrow{CM}(t)\wedge m[\overrightarrow{\mathrm{\Omega }}(t)\wedge \overrightarrow{CM}(t)]$

» nécessitant d'utiliser une des deux formules du double produit vectoriel soit «

$\frac{{\overrightarrow{\sigma }}_C(M,t)}{m}$ $=\stackrel{2}{\overrightarrow{CM}}(t)\overrightarrow{\mathrm{\Omega }}(t)\cancel{-[\overrightarrow{CM}(t)\cdot \overrightarrow{\mathrm{\Omega }}(t)]\overrightarrow{CM}(t)}$

» car, de par la nature du mouvement de

$M$

« le rayon vecteur

$\overrightarrow{CM}(t)$

est

$\perp$

à

$\overrightarrow{\mathrm{\Omega }}(t)$

à tout instant », soit encore, en notant

$R$

le rayon du cercle

$\Rightarrow$ $\stackrel{2}{\overrightarrow{CM}}(t)=R^2\mathrm{\forall }t$

, l'expression finale du vecteur moment cinétique du point matériel

$M$

en mouvement circulaire de centre

$C$

, de rayon

$R$

et de vecteur rotation instantanée

$\overrightarrow{\mathrm{\Omega }}(t)$

quand l'origine de calcul du moment cinétique est le centre

$C$

du cercle

«${\overrightarrow{\sigma }}_C(M,t)=m{R}^2\overrightarrow{\mathrm{\Omega }}(t)$».

Notion de moment d'inertie de M relativement à un axe Δ

Modèle:AlLe moment d'inertie d'un point matériel

$M$

, de masse

$m$

, relativement à un axe

$\mathrm{\Delta }$

est introduit quand le point

$M$

« tourne » autour de l'axe

$\mathrm{\Delta }$

, il est noté «

$J_{\mathrm{\Delta }}(M)$

» et représente une « grandeur scalaire inertielle de rotation », il est défini par la relation

«$J_{\mathrm{\Delta }}(M)=m{r}^2$ exprimé en $kg\cdot m^2$»,
dans laquelle «$m$ est la masse du point » et «$r$ la distance orthogonale séparant $M$ de l'axe $\mathrm{\Delta }$».

Réécriture du vecteur moment cinétique de M en mouvement circulaire dans le référentiel d’étude par rapport au centre C du cercle en fonction, entre autres, du vecteur rotation instantanée

Modèle:AlLe vecteur moment cinétique du point matériel

$M$

dans le référentiel d'étude

$ℛ$

par rapport au centre

$C$

du cercle

$($

« support de la trajectoire de

$M$

»

$)$

s'écrit

«${\overrightarrow{\sigma }}_C(M,t)=J_{\mathrm{\Delta }}(M)\overrightarrow{\mathrm{\Omega }}(t)$» où
«$J_{\mathrm{\Delta }}(M)=m{R}^2$ est le moment d'inertie de $M$ relativement à l'axe de rotation $\mathrm{\Delta }$»,
«$m$ étant la masse du point », «$R$ le rayon du cercle » et
«$\overrightarrow{\mathrm{\Omega }}(t)$ le vecteur rotation instantanée du mouvement circulaire du point $M$».

Évaluation du vecteur moment cinétique de M en mouvement circulaire dans le référentiel d’étude par rapport à un point A de l’axe de rotation, différent du centre C du cercle

Schéma descriptif du mouvement d'un point matériel $M$ décrivant un cercle de centre $C$, de vecteur rotation instantanée $\overrightarrow{\mathrm{\Omega }}(t)$, avec précision du vecteur moment cinétique ${\overrightarrow{\sigma }}_A(M,t)$ de $M$ en un point $($origine de calcul de moment cinétique$)$ $A$ de l'axe de rotation mais différent du centre $C$

Modèle:AlSoit «

$A$

un point quelconque de l'axe

$\mathrm{\Delta }$

de rotation du point matériel

$M$

» avec «

$A\ne C$

centre du cercle décrit par

$M$

dans le référentiel

$ℛ$ $($

orienté à droite

$)$

avec pour vecteur rotation instantanée

$\overrightarrow{\mathrm{\Omega }}(t)$

», « le vecteur moment cinétique du point matériel

$M$

dans

$ℛ$

par rapport au point

$A\ne C$

de son axe de rotation, noté

${\overrightarrow{\sigma }}_A(M,t)$

» est défini par

«${\overrightarrow{\sigma }}_A(M,t)=\overrightarrow{AM}(t)\wedge {\overrightarrow{p}}_M(t)$» ou,
dans le cadre de la cinétique classique, «${\overrightarrow{\sigma }}_A(M,t)=\overrightarrow{AM}(t)\wedge m{\overrightarrow{V}}_M(t)$» ;

Modèle:Alinjectant dans cette dernière expression de

${\overrightarrow{\sigma }}_C(M,t)$

du cadre de la cinétique classique, l'expression intrinsèque du vecteur vitesse d'un point en mouvement circulaire de centre

$C$

et de vecteur rotation instantanée

$\overrightarrow{\mathrm{\Omega }}(t)$

, à savoir «

${\overrightarrow{V}}_M(t)=$ $\overrightarrow{\mathrm{\Omega }}(t)\wedge \overrightarrow{CM}(t)$

»Modèle:,, on obtient «

${\overrightarrow{\sigma }}_A(M,t)=$ $\overrightarrow{AM}(t)\wedge m[\overrightarrow{\mathrm{\Omega }}(t)\wedge \overrightarrow{CM}(t)]$

» nécessitant d'utiliser une des deux formules du double produit vectoriel soit «

$\frac{{\overrightarrow{\sigma }}_A(M,t)}{m}$ $=[\overrightarrow{AM}(t)\cdot \overrightarrow{CM}(t)]\overrightarrow{\mathrm{\Omega }}(t)-[\overrightarrow{AM}(t)\cdot \overrightarrow{\mathrm{\Omega }}(t)]\overrightarrow{CM}(t)$

» avec «

$\overrightarrow{AM}(t)=\overrightarrow{AC}(t)+\overrightarrow{CM}(t)$

» utilisant la relation de Chasles ou, en notant

${\overrightarrow{u}}_{\mathrm{\Delta }}$

le vecteur unitaire de

$\mathrm{\Delta }$ $\Rightarrow$ $\left\{\begin{array}{c}\overrightarrow{\mathrm{\Omega }}(t)=\bar{\mathrm{\Omega }}(t){\overrightarrow{u}}_{\mathrm{\Delta }}\text{ainsi que}\\ \overrightarrow{AM}(t)=\overline{AC}{\overrightarrow{u}}_{\mathrm{\Delta }}+\overrightarrow{CM}(t)\end{array}\right\}$ $\Rightarrow$ $\left\{\begin{array}{c}\overrightarrow{AM}(t)\cdot \overrightarrow{\mathrm{\Omega }}(t)=\overline{AC}\bar{\mathrm{\Omega }}(t)\cancel{+\overrightarrow{CM}(t)\cdot \bar{\mathrm{\Omega }}(t){\overrightarrow{u}}_{\mathrm{\Delta }}}\\ \overrightarrow{AM}(t)\cdot \overrightarrow{CM}(t)=\cancel{\overline{AC}{\overrightarrow{u}}_{\mathrm{\Delta }}\cdot \overrightarrow{CM}(t)+}\stackrel{2}{\overrightarrow{CM}}(t)\end{array}\right\}$ $[\overrightarrow{CM}(t)$

étant

$\perp$

à

${\overrightarrow{u}}_{\mathrm{\Delta }}]$

d'où «

$\frac{{\overrightarrow{\sigma }}_A(M,t)}{m}=\stackrel{2}{\overrightarrow{CM}}(t)\overrightarrow{\mathrm{\Omega }}(t)-\overline{AC}\bar{\mathrm{\Omega }}(t)\overrightarrow{CM}(t)$

», soit encore, en notant

$R$

le rayon du cercle

$\Rightarrow$ $\stackrel{2}{\overrightarrow{CM}}(t)=R^2\mathrm{\forall }t$

, l'expression finale du vecteur moment cinétique du point matériel

$M$

en mouvement circulaire de centre

$C$

, de rayon

$R$

et de vecteur rotation instantanée

$\overrightarrow{\mathrm{\Omega }}(t)$

quand l'origine de calcul du moment cinétique est un point

$A$

de l'axe de rotation

$\ne$

du centre

$C$

du cercle

«${\overrightarrow{\sigma }}_A(M,t)=m{R}^2\overrightarrow{\mathrm{\Omega }}(t)-m\bar{\mathrm{\Omega }}(t)\overline{AC}\overrightarrow{CM}(t)$»,

Modèle:Alsoit une somme de deux termes dont

• le 1^er «$m{R}^2\overrightarrow{\mathrm{\Omega }}(t)={\overrightarrow{\sigma }}_C(M,t)=J_{\mathrm{\Delta }}(M)\overrightarrow{\mathrm{\Omega }}(t)$» est colinéaire à l'axe de rotation et
• le 2^nd «$-m\bar{\mathrm{\Omega }}(t)\overline{AC}\overrightarrow{CM}(t)={\overrightarrow{\sigma }}_{A,\perp \text{à}\mathrm{\Delta }}(M,t)$» est $\perp$ à l'axe de rotation dans le « plan méridien de $M$»,

Modèle:Alce qu'on peut encore écrire

«${\overrightarrow{\sigma }}_A(M,t)={\overrightarrow{\sigma }}_C(M,t)+{\overrightarrow{\sigma }}_{A,\perp \text{à}\mathrm{\Delta }}(M,t)$».

Modèle:AlRemarque : « la relation de proportionnalité entre ${\overrightarrow{\sigma }}_A(M,t)$ et $\overrightarrow{\mathrm{\Omega }}(t)$ n'est réalisée qu'en choisissant pour origine de calcul du moment cinétique le centre $C$ du cercle », et qu'« en dehors de ce point $C$, il n'y a pas proportionnalité entre ${\overrightarrow{\sigma }}_A(M,t)$ et $\overrightarrow{\mathrm{\Omega }}(t)$» car « pour $A\ne C$, ${\overrightarrow{\sigma }}_A(M,t)$ n’est pas porté par l'axe $\mathrm{\Delta }$».

Analogie entre la cinétique d’un point matériel en mouvement quelconque et celle d’un point matériel en mouvement de rotation autour d’un axe Δ

Modèle:AlEn cinétique classique d'un point matériel en mouvement quelconque, il existe un facteur de proportionnalité entre la « grandeur cinétique

${\overrightarrow{p}}_M(t)$

» et la « grandeur cinématique

${\overrightarrow{V}}_M(t)$

», ce facteur égal à la masse du point matériel «

$m$

représentant la grandeur d'inertie » soit

$\begin{array}{ccccc}{\overrightarrow{p}}_M(t)& =& m& \times & {\overrightarrow{V}}_M(t)\\ \text{« grandeur cinétique}& =& \text{grandeur d'inertie}& \times & \text{grandeur cinématique » ;}\end{array}$

Modèle:Alen cinétique classique d'un point matériel de masse

$m$

en mouvement circulaire d'axe

$\mathrm{\Delta }$

, de centre

$C$

et de rayon

$R$

, on trouve une relation de proportionnalité analogue entre la « grandeur cinétique

${\overrightarrow{\sigma }}_C(M,t)$

» et la « grandeur cinématique

$\overrightarrow{\mathrm{\Omega }}(t)$

», le facteur de proportionnalité égal au moment d'inertie du point matériel relativement à l'axe de rotation «

$J_{\mathrm{\Delta }}(M)=m{R}^2$

représentant la grandeur d'inertie » soit

$\begin{array}{ccccc}{\overrightarrow{\sigma }}_C(M,t)& =& J_{\mathrm{\Delta }}(M)& \times & \overrightarrow{\mathrm{\Omega }}(t)\\ \text{« grandeur cinétique}& =& \text{grandeur d'inertie}& \times & \text{grandeur cinématique » ;}\end{array}$

Modèle:Alon vérifie ainsi l'analogie de cinétique classique entre mouvements de translation et de rotation suivant les correspondances suivantes

«$\begin{array}{cccccc}\text{translation}& {\overrightarrow{p}}_M(t)& =& m& \times & {\overrightarrow{V}}_M(t)\\ & \updownarrow & & \updownarrow & & \updownarrow \\ \text{rotation}& {\overrightarrow{\sigma }}_C(M,t)& =& J_{\mathrm{\Delta }}(M)& \times & \overrightarrow{\mathrm{\Omega }}(t)\end{array}$».

Complément, expression relativiste du vecteur moment cinétique de M en mouvement circulaire dans le référentiel d’étude par rapport au centre C du cercle

Modèle:AlComme cela a été établi dans le paragraphe « complément, expression relativiste du vecteur moment cinétique de M dans le référentiel d'étude par rapport au point origine A » plus haut dans ce chapitre, le vecteur moment cinétique

${\overrightarrow{\sigma }}_{A,\text{relativ}}(M,t)$

du point matériel

$M$

en mouvement relativiste dans le référentiel d'étude

$ℛ$

orienté à droite par rapport à un point origine

$A$

est lié à l'expression que le vecteur moment cinétique

${\overrightarrow{\sigma }}_{A,\text{newton}}(M,t)$

du point matériel

$M$

prendrait si le mouvement de ce dernier était classique dans le même référentiel d'étude

$ℛ$

par rapport au même point origine

$A$

selon

«${\overrightarrow{\sigma }}_{A,\text{relativ}}(M,t)={\gamma }_M(t){\overrightarrow{\sigma }}_{A,\text{newton}}(M,t)$»
avec «${\gamma }_M(t)=\frac{1}{\sqrt{1-{\left[\frac{\Vert {\overrightarrow{V}}_M(t)\Vert }{c}\right]}^2}}$ facteur de Lorentz du point $M$ dans $ℛ$» ;

Modèle:Aldans le référentiel d'étude $ℛ$, le vecteur moment cinétique du point matériel $M$ en mouvement circulaire classique autour de l'axe $\mathrm{\Delta }$ de rotation, de centre $C$, de rayon $R$ et de vecteur rotation instantanée $\overrightarrow{\mathrm{\Omega }}(t)$, avec, pour point origine de calcul du moment, le centre $C$ du cercle, ayant pour expression établie précédemment «${\overrightarrow{\sigma }}_{C,\text{newton}}(M,t)=$ $J_{\mathrm{\Delta }}(M)\overrightarrow{\mathrm{\Omega }}(t)$» dans laquelle «$J_{\mathrm{\Delta }}(M)=$ $m{R}^2$ est le moment d'inertie du point $M$ autour de son axe de rotation $\mathrm{\Delta }$» et

Modèle:AlModèle:Transparentla définition du vecteur rotation instantanée $\overrightarrow{\mathrm{\Omega }}(t)$ ainsi que son lien avec le vecteur vitesse ${\overrightarrow{V}}_M(t)$ dans un mouvement circulaire de centre $C$ à savoir ${\overrightarrow{V}}_M(t)=$ $\overrightarrow{\mathrm{\Omega }}(t)\wedge \overrightarrow{CM}(t)$ restant les mêmes en relativiste, on en déduit l'expression du facteur de Lorentz du point $M$ dans $ℛ$ en fonction de la vitesse angulaire non algébrisée $\Vert \overrightarrow{\mathrm{\Omega }}(t)\Vert$ et du rayon $R$ du cercle soit Modèle:Nobr $\frac{1}{\sqrt{1-{\left[\frac{R\Vert \overrightarrow{\mathrm{\Omega }}(t)\Vert }{c}\right]}^2}}$» d'où

Modèle:AlModèle:Transparentl'expression du vecteur moment cinétique du point matériel

$M$

en mouvement circulaire relativiste autour de l'axe

$\mathrm{\Delta }$

de rotation, de centre

$C$

, de rayon

$R$

et de vecteur rotation instantanée

$\overrightarrow{\mathrm{\Omega }}(t)$

, avec, pour point origine de calcul du moment, le centre

$C$

du cercle,

«${\overrightarrow{\sigma }}_{C,\text{relativ}}(M,t)={\gamma }_M(t){\overrightarrow{\sigma }}_{C,\text{newton}}(M,t)={\gamma }_M(t)J_{\mathrm{\Delta }}(M)\overrightarrow{\mathrm{\Omega }}(t)$» avec
«$J_{\mathrm{\Delta }}(M)=m{R}^2$ le moment d'inertie du point $M$ autour de son axe de rotation $\mathrm{\Delta }$» et
«${\gamma }_M(t)=\frac{1}{\sqrt{1-{\left[\frac{R\Vert \overrightarrow{\mathrm{\Omega }}(t)\Vert }{c}\right]}^2}}$ le facteur de Lorentz du point $M$ dans $ℛ$».

Modèle:AlRemarque 1 : en cinétique relativiste d'un point matériel de masse

$m$

en mouvement quelconque, il existe un facteur de proportionnalité entre la « grandeur cinétique

${\overrightarrow{p}}_M(t)$

» et la « grandeur cinématique

${\gamma }_M(t){\overrightarrow{V}}_M(t)=\frac{{\overrightarrow{V}}_M(t)}{\sqrt{1-{\left[\frac{\Vert {\overrightarrow{V}}_M(t)\Vert }{c}\right]}^2}}$

», ce facteur égal à la masse du point matériel «

$m$

représentant la grandeur d'inertie » soit

«$\begin{array}{ccccc}{\overrightarrow{p}}_M(t)& =& m& \times & {\gamma }_M(t){\overrightarrow{V}}_M(t)\\ & & \text{ou}& & \\ {\overrightarrow{p}}_M(t)& =& m& \times & \frac{{\overrightarrow{V}}_M(t)}{\sqrt{1-{\left[\frac{\Vert {\overrightarrow{V}}_M(t)\Vert }{c}\right]}^2}}\\ \text{grandeur cinétique}& =& \text{grandeur d'inertie}& \times & \text{grandeur cinématique}\end{array}$» ;

Modèle:AlModèle:Transparenten cinétique relativiste d'un point matériel de masse

$m$

en mouvement circulaire d'axe

$\mathrm{\Delta }$

, de centre

$C$

et de rayon

$R$

, on trouve une relation de proportionnalité analogue entre la « grandeur cinétique

${\overrightarrow{\sigma }}_{C,\text{relativ}}(M,t)$

» et la « grandeur cinématique

${\gamma }_M(t)\overrightarrow{\mathrm{\Omega }}(t)=$ $\frac{\overrightarrow{\mathrm{\Omega }}(t)}{\sqrt{1-{\left[\frac{R\Vert \overrightarrow{\mathrm{\Omega }}(t)\Vert }{c}\right]}^2}}$

», le facteur de proportionnalité égal au moment d'inertie du point matériel relativement à l'axe de rotation «

$J_{\mathrm{\Delta }}(M)=m{R}^2$

représentant la grandeur d'inertie » soit

«$\begin{array}{ccccc}{\overrightarrow{\sigma }}_{C,\text{relativ}}(M,t)& =& J_{\mathrm{\Delta }}(M)& \times & {\gamma }_M(t)\overrightarrow{\mathrm{\Omega }}(t)\\ & & \text{ou}& & \\ {\overrightarrow{\sigma }}_{C,\text{relativ}}(M,t)& =& J_{\mathrm{\Delta }}(M)& \times & \frac{\overrightarrow{\mathrm{\Omega }}(t)}{\sqrt{1-{\left[\frac{R\Vert \overrightarrow{\mathrm{\Omega }}(t)\Vert }{c}\right]}^2}}\\ \text{grandeur cinétique}& =& \text{grandeur d'inertie}& \times & \text{grandeur cinématique}\end{array}$» ;

Modèle:AlRemarque 2 : dans le but de garder les mêmes grandeurs cinématiques en cinétiques classique et relativiste, on peut introduire des « grandeurs d'inertie apparentes » c'est-à-dire
Modèle:AlModèle:Transparent$\succ$la « masse apparente $m_{\text{app}}={\gamma }_M(t)m=\frac{m}{\sqrt{1-{\left[\frac{\Vert {\overrightarrow{V}}_M(t)\Vert }{c}\right]}^2}}$» $\Rightarrow$ «${\overrightarrow{p}}_M(t)=m_{\text{app}}{\overrightarrow{V}}_M(t)$ en translation relativiste » et
Modèle:AlModèle:Transparent$\succ$le « moment d'inertie apparent $J_{\mathrm{\Delta },\text{app}}(M)={\gamma }_M(t)J_{\mathrm{\Delta }}(M)=\frac{J_{\mathrm{\Delta }}(M)}{\sqrt{1-{\left[\frac{R\Vert \overrightarrow{\mathrm{\Omega }}(t)\Vert }{c}\right]}^2}}$ $[$ou $J_{\mathrm{\Delta },\text{app}}(M)=m_{\text{app}}{R}^2]$» $\Rightarrow$ «${\overrightarrow{\sigma }}_{C,\text{relativ}}(M,t)=$ $J_{\mathrm{\Delta },\text{app}}(M)\overrightarrow{\mathrm{\Omega }}(t)$ en rotation relativiste ».

Aspect de la cinétique de M dans le référentiel d’étude relativement à un axe Δ, définition dans ce référentiel du moment cinétique de M par rapport à l’axe Δ (ou « moment cinétique scalaire de M »)

Notion d’« équiprojectivité » du « champ de vecteurs moment d’un champ vectoriel »

Modèle:AlCette notion introduite pour un champ de vecteurs

$\overrightarrow{f}(M)$

dans le paragraphe « définition de l'équiprojectivité d'un champ de vecteurs d'un espace affine euclidien tridimensionnel

$ℰ$

» du chap.

$1$

de la leçon « Outils mathématiques pour la physique - bis (PCSI) » à savoir

«$\mathrm{\forall }(M,N)\in {ℰ}^2,\overrightarrow{f}(M)\cdot \overrightarrow{MN}=\overrightarrow{f}(N)\cdot \overrightarrow{MN}$»,

Modèle:Aln'est pas vérifiée pour n'importe quel champ de vecteurs mais $\dots$

Modèle:Alcette propriété d’« équiprojectivité » est « applicable au champ de vecteurs moment d'un champ vectoriel quelconque

$\overrightarrow{C}(M)$

défini par

$\mathrm{\forall }P\in ℰ$

,

${\overrightarrow{ℳ}}_P[\overrightarrow{C}(M)]=\overrightarrow{PM}\wedge \overrightarrow{C}(M)$

», en effet Modèle:Nobr

${\overrightarrow{ℳ}}_P[\overrightarrow{C}(M)]\cdot \overrightarrow{PQ}\stackrel{\text{?}}{=}{\overrightarrow{ℳ}}_Q[\overrightarrow{C}(M)]\cdot \overrightarrow{PQ}$

»

$\iff$

«

$[\overrightarrow{PM}\wedge \overrightarrow{C}(M)]\cdot \overrightarrow{PQ}\stackrel{\text{?}}{=}$ $[\overrightarrow{QM}\wedge \overrightarrow{C}(M)]\cdot \overrightarrow{PQ}$ $\iff$ $\{[\overrightarrow{PQ}+\overrightarrow{QM}]\wedge \overrightarrow{C}(M)\}\cdot \overrightarrow{PQ}\stackrel{\text{?}}{=}$ $[\overrightarrow{QM}\wedge \overrightarrow{C}(M)]\cdot \overrightarrow{PQ}$

» par utilisation de la relation de Chasles soit enfin, en utilisant la distributivité de la multiplication vectorielle par rapport à l'addition vectorielle dans le 1^er membre de cette équation que l'on cherche à vérifier Modèle:Nobr

$\stackrel{\cancel{\text{?}}}{=}[\overrightarrow{QM}\wedge \overrightarrow{C}(M)]\cdot \overrightarrow{PQ}$

» ce qui établit la propriété d’« équiprojectivité » compte-tenu de la nullité du 1^er produit mixte du 1^er membre ;

en conclusion on retient «$\mathrm{\forall }(P,Q)\in {ℰ}^2,{\overrightarrow{ℳ}}_P[\overrightarrow{C}(M)]\cdot \overrightarrow{PQ}={\overrightarrow{ℳ}}_Q[\overrightarrow{C}(M)]\cdot \overrightarrow{PQ}\mathrm{\forall }\overrightarrow{C}(M)$».

Équiprojectivité du « vecteur champ moment cinétique de M » dans le référentiel d’étude et conséquence, notion de « moment cinétique de M dans le référentiel d'étude par rapport à un axe Δ »

Modèle:AlLe « vecteur moment cinétique du point matériel

$M$

dans le référentiel

$ℛ$

par rapport à

$A$ $($

point origine de calcul du moment cinétique

$)$

» étant le « vecteur moment du champ vectoriel quantité de mouvement

${\overrightarrow{p}}_M$

du point matériel

$M$

dans le référentiel

$ℛ$

par rapport à

$A$ $($

point origine de calcul du moment

$)$

», nous en déduisons l'« équiprojectivité du vecteur champ moment cinétique du point matériel

$M$

» dans le référentiel d’étude soit

«$\mathrm{\forall }(A,A^{\prime })\in {ℰ}^2,{\overrightarrow{\sigma }}_A(M,t)\cdot \overrightarrow{A{A}^{\prime }}={\overrightarrow{\sigma }}_{A^{\prime }}(M,t)\cdot \overrightarrow{A{A}^{\prime }}$».

Modèle:AlRemarque : avec la notion $($hors programme de physique de P.C.S.I.$)$ de « torseur » introduite dans le chap.$1$ de la leçon « Outils mathématiques pour la physique - bis (PCSI) », le vecteur moment cinétique du point matériel $M$ par rapport à $A$ «${\overrightarrow{\sigma }}_A(M,t)$» étant le moment du torseur cinétique de $M$ «${𝒯}_{\text{cinét. de}M}$» d'éléments de réduction en $A$ Modèle:Nobr ${\left\{\begin{array}{c}{\overrightarrow{p}}_M(t)=m{\overrightarrow{V}}_M(t)\\ {\overrightarrow{\sigma }}_A(M,t)=\overrightarrow{AM}(t)\wedge {\overrightarrow{p}}_M(t)\end{array}\right\}}_A$» et
Modèle:AlModèle:Transparentle « moment d'un torseur au point $A$» étant par définition un « champ de vecteurs équiprojectif » nous en déduisons, sans autre développement, le caractère « équiprojectif » du « vecteur moment cinétique du point matériel $M$ dans le référentiel $ℛ$ par rapport à $A$».

Modèle:AlConséquence : considérant un axe $\mathrm{\Delta }$ quelconque et deux points quelconques $($distincts$)$ de cet axe $(A,A^{\prime }\ne A)\in {\mathrm{\Delta }}^2$, nous déduisons de l'équiprojectivité du vecteur moment cinétique du point matériel $M$ dans le référentiel $ℛ$ la relation «${\overrightarrow{\sigma }}_A(M,t)\cdot \overrightarrow{A{A}^{\prime }}={\overrightarrow{\sigma }}_{A^{\prime }}(M,t)\cdot \overrightarrow{A{A}^{\prime }}$» ou,
Modèle:AlModèle:Transparenten orientant l'axe $\mathrm{\Delta }$ par ${\overrightarrow{u}}_{\mathrm{\Delta }}$ $\Rightarrow$ «$\overrightarrow{A{A}^{\prime }}=\overline{A{A}^{\prime }}{\overrightarrow{u}}_{\mathrm{\Delta }}$» et en simplifiant par $\overline{A{A}^{\prime }}\ne 0$, «${\overrightarrow{\sigma }}_A(M,t)\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}={\overrightarrow{\sigma }}_{A^{\prime }}(M,t)\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}$» cette valeur constante sur $\mathrm{\Delta }$ définissant le moment cinétique $($scalaire$)$ du point matériel $M$ dans le référentiel d'étude $ℛ$ par rapport à l'axe $\mathrm{\Delta }$. Modèle:Définition Modèle:AlCommentaire : cette grandeur traduit la réserve de « mouvement inertiel » du point matériel $M$ par rapport à l'axe $\mathrm{\Delta }$, elle tient compte de l'inertie d'une part et de la composante de la vitesse dans un plan $\perp$ à $\mathrm{\Delta }$ ainsi que de la disposition du point $M$ par rapport à cet axe d'autre part, la grandeur dépend donc du référentiel $(ℛ)$.

Retour sur le cas où M décrit un mouvement circulaire d’axe Δ, de rayon R et de vecteur rotation instantanée fixé

Évaluation du moment cinétique de M en mouvement circulaire dans le référentiel d’étude par rapport à l’axe Δ du cercle

Modèle:AlLe vecteur moment cinétique du point matériel $M$, de masse $m$, par rapport au centre $C$ du cercle $($« support de la trajectoire de $M$»$)$ de rayon $R$ dans le référentiel d'étude $ℛ$ s'écrivant «${\overrightarrow{\sigma }}_C(M,t)=J_{\mathrm{\Delta }}(M)\overrightarrow{\mathrm{\Omega }}(t)$» avec «$J_{\mathrm{\Delta }}(M)=m{R}^2$ le moment d'inertie du point $M$ relativement à l'axe $\mathrm{\Delta }$» et «$\overrightarrow{\mathrm{\Omega }}(t)$ le vecteur rotation instantanée du mouvement du point », nous en déduisons

Modèle:Alaprès orientation de l'axe $\mathrm{\Delta }$ par ${\overrightarrow{u}}_{\mathrm{\Delta }}$ $\Rightarrow$ «$\overrightarrow{\mathrm{\Omega }}(t)=\bar{\mathrm{\Omega }}(t){\overrightarrow{u}}_{\mathrm{\Delta }}$» dans laquelle «$\bar{\mathrm{\Omega }}(t)$ est la vitesse angulaire de rotation du point $M$ sur le cercle »,

Modèle:All'expression du moment cinétique

$($

scalaire

$)$

du point matériel

$M$

par rapport à l'axe

$\mathrm{\Delta }$

du cercle, à l'instant

$t$

, dans le référentiel d'étude

$ℛ$

, «

${\sigma }_{\mathrm{\Delta }}(M,t)={\overrightarrow{\sigma }}_C(M,t)\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}=J_{\mathrm{\Delta }}(M)\overrightarrow{\mathrm{\Omega }}(t)\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}$

» soit finalement

«${\sigma }_{\mathrm{\Delta }}(M,t)=J_{\mathrm{\Delta }}(M)\bar{\mathrm{\Omega }}(t)$».

Modèle:AlRemarque : Le moment cinétique $($scalaire$)$ de $M$ par rapport à l'axe $\mathrm{\Delta }$ de rotation de son mouvement circulaire étant la projection sur $\mathrm{\Delta }$ orienté par ${\overrightarrow{u}}_{\mathrm{\Delta }}$ du moment cinétique $($vectoriel$)$ de $M$ par rapport à n'importe quel point de $\mathrm{\Delta }$, on vérifie qu'en prenant un point origine $A\in \mathrm{\Delta }$ $($avec $A\ne$ $C$ centre du cercle$)$ on trouve le même résultat, en effet
Modèle:AlModèle:Transparentayant établi précédemment «${\overrightarrow{\sigma }}_A(M,t)={\overrightarrow{\sigma }}_C(M,t)+{\overrightarrow{\sigma }}_{A,\perp \text{à}\mathrm{\Delta }}(M,t)$» et multipliant scalairement par ${\overrightarrow{u}}_{\mathrm{\Delta }}$ on obtient, après utilisation de la distributivité du produit scalaire relativement à l’addition vectorielle, «${\overrightarrow{\sigma }}_A(M,t)\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}={\overrightarrow{\sigma }}_C(M,t)\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}\cancel{+{\overrightarrow{\sigma }}_{A,\perp \text{à}\mathrm{\Delta }}(M,t)\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}}$», « le 2^ème terme du 2^ème membre étant nul car ${\overrightarrow{\sigma }}_{A,\perp \text{à}\mathrm{\Delta }}(M,t)$ est $\perp$ à ${\overrightarrow{u}}_{\mathrm{\Delta }}$» et « le 1^er terme restant du 2^ème membre étant égal à $J_{\mathrm{\Delta }}(M)\bar{\mathrm{\Omega }}(t)$».

Expression symbolique reliant la cinétique et la cinématique dans le cas d’un mouvement circulaire autour d’un axe Δ

Modèle:AlEn cinétique classique d'un point matériel de masse

$m$

en mouvement circulaire d'axe

$\mathrm{\Delta }$

et de rayon

$R$

, on trouve une relation de proportionnalité analogue à celles exposées au paragraphe « analogie entre la cinétique d'un point matériel en mouvement quelconque et celle d'un point matériel en mouvement de rotation autour d'un axe Δ » plus haut dans ce chapitre entre la « grandeur cinétique “moment cinétique scalaire”

${\sigma }_{\mathrm{\Delta }}(M,t)$

du point » et la « grandeur cinématique “vitesse angulaire de rotation”

$\bar{\mathrm{\Omega }}(t)$

du point », le facteur de proportionnalité égal au moment d'inertie du point matériel relativement à l'axe de rotation «

$J_{\mathrm{\Delta }}(M)=m{R}^2$

représentant la grandeur d'inertie » soit

$\begin{array}{ccccc}{\sigma }_{\mathrm{\Delta }}(M,t)& =& J_{\mathrm{\Delta }}(M)& \times & \bar{\mathrm{\Omega }}(t)\\ \text{« grandeur cinétique}& =& \text{grandeur d'inertie}& \times & \text{grandeur cinématique » ;}\end{array}$

Modèle:Alon vérifie ainsi l'analogie de cinétique classique entre mouvements de translation et de rotation suivant les correspondances suivantes

«$\begin{array}{cccccc}\text{translation}& {\overrightarrow{p}}_M(t)& =& m& \times & {\overrightarrow{V}}_M(t)\\ & \updownarrow & & \updownarrow & & \updownarrow \\ \text{rotation}& {\sigma }_{\mathrm{\Delta }}(M,t)& =& J_{\mathrm{\Delta }}(M)& \times & \bar{\mathrm{\Omega }}(t)\end{array}$».

Complément, expression relativiste du moment cinétique de M en mouvement circulaire dans le référentiel d’étude par rapport à l’axe Δ du cercle

Modèle:AlAyant établi, plus haut dans ce chapitre, au paragraphe « complément, expression relativiste du vecteur moment cinétique de M en mouvement circulaire dans le référentiel d'étude par rapport au centre C du cercle », l'expression du vecteur moment cinétique du point matériel

$M$

en mouvement circulaire relativiste autour de l'axe

$\mathrm{\Delta }$

de rotation dans le référentiel d'étude

$ℛ$

, le point origine de calcul du vecteur moment cinétique étant le centre

$C$

du cercle,

«${\overrightarrow{\sigma }}_{C,\text{relativ}}(M,t)={\gamma }_M(t){\overrightarrow{\sigma }}_{C,\text{newton}}(M,t)={\gamma }_M(t)J_{\mathrm{\Delta }}(M)\overrightarrow{\mathrm{\Omega }}(t)$»

Modèle:Aldans laquelle «$\overrightarrow{\mathrm{\Omega }}(t)$ est le vecteur rotation instantanée », «$J_{\mathrm{\Delta }}(M)$ le moment d'inertie du point $M$ autour de son axe de rotation $\mathrm{\Delta }$» et «${\gamma }_M(t)=$ $\frac{1}{\sqrt{1-{\left[\frac{R\Vert \overrightarrow{\mathrm{\Omega }}(t)\Vert }{c}\right]}^2}}$ le facteur de Modèle:Nobr du point $M$ dans le référentiel d'étude $ℛ$», il suffit, pour établir l'expression relativiste du moment cinétique scalaire ${\sigma }_{\mathrm{\Delta },\text{relativ}}(M,t)$ du point matériel $M$ en mouvement circulaire d'axe $\mathrm{\Delta }$, ce dernier étant l'axe par rapport auquel le moment cinétique scalaire est évalué, de projeter ${\overrightarrow{\sigma }}_{C,\text{relativ}}(M,t)$ sur le vecteur unitaire ${\overrightarrow{u}}_{\mathrm{\Delta }}$ orientant l'axe $\mathrm{\Delta }$, d'où

Modèle:Al«

${\sigma }_{\mathrm{\Delta },\text{relativ}}(M,t)={\overrightarrow{\sigma }}_{C,\text{relativ}}(M,t)\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}=[{\gamma }_M(t){\overrightarrow{\sigma }}_{C,\text{newton}}(M,t)]\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}={\gamma }_M(t)[{\overrightarrow{\sigma }}_{C,\text{newton}}(M,t)\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}]$

» soit encore, en reconnaissant dans l'expression entre crochets le moment cinétique scalaire

${\sigma }_{\mathrm{\Delta },\text{newton}}(M,t)$

que le point matériel en mouvement circulaire d'axe

$\mathrm{\Delta }$

aurait en cinétique classique, la relation suivante, dans le référentiel d'étude

$ℛ$

,

«${\sigma }_{\mathrm{\Delta },\text{relativ}}(M,t)={\gamma }_M(t){\sigma }_{\mathrm{\Delta },\text{newton}}(M,t)={\gamma }_M(t)J_{\mathrm{\Delta }}(M)\bar{\mathrm{\Omega }}(t)$» avec
«${\gamma }_M(t)=\frac{1}{\sqrt{1-{\left[\frac{R\bar{\mathrm{\Omega }}(t)}{c}\right]}^2}}$ le facteur de Lorentz du point $M$»,
«$J_{\mathrm{\Delta }}(M)$ le moment d'inertie du point $M$ autour de son axe de rotation $\mathrm{\Delta }$» et
«$\bar{\mathrm{\Omega }}(t)$ la vitesse angulaire de rotation de $M$ sur le cercle ».

Modèle:AlRemarque 1 : en cinétique relativiste d'un point matériel de masse

$m$

en mouvement circulaire d'axe

$\mathrm{\Delta }$

, de centre

$C$

et de rayon

$R$

, on trouve une relation de proportionnalité analogue à celles exposées dans le paragraphe plus haut dans ce chapitre, entre la « grandeur cinétique

${\sigma }_{\mathrm{\Delta },\text{relativ}}(M,t)$

» et la « grandeur cinématique

${\gamma }_M(t)\bar{\mathrm{\Omega }}(t)=$ $\frac{\bar{\mathrm{\Omega }}(t)}{\sqrt{1-{\left[\frac{R\bar{\mathrm{\Omega }}(t)}{c}\right]}^2}}$

», le facteur de proportionnalité égal au moment d'inertie du point matériel relativement à l'axe de rotation «

$J_{\mathrm{\Delta }}(M)=m{R}^2$

représentant la grandeur d'inertie » soit

«$\begin{array}{ccccc}{\sigma }_{\mathrm{\Delta },\text{relativ}}(M,t)& =& J_{\mathrm{\Delta }}(M)& \times & {\gamma }_M(t)\bar{\mathrm{\Omega }}(t)\\ & & \text{ou}& & \\ {\sigma }_{\mathrm{\Delta },\text{relativ}}(M,t)& =& J_{\mathrm{\Delta }}(M)& \times & \frac{\bar{\mathrm{\Omega }}(t)}{\sqrt{1-{\left[\frac{R\bar{\mathrm{\Omega }}(t)}{c}\right]}^2}}\\ \text{grandeur cinétique}& =& \text{grandeur d'inertie}& \times & \text{grandeur cinématique}\end{array}$».

Modèle:AlRemarque 2 : là encore, dans le but de garder les mêmes grandeurs cinématiques en cinétiques classique et relativiste, on peut introduire des « grandeurs d'inertie apparentes » Modèle:Nobr
Modèle:AlModèle:Transparent$\succ$la « masse apparente $m_{\text{app}}={\gamma }_M(t)m=\frac{m}{\sqrt{1-{\left[\frac{\Vert {\overrightarrow{V}}_M(t)\Vert }{c}\right]}^2}}$» $\Rightarrow$ «${\overrightarrow{p}}_M(t)=m_{\text{app}}{\overrightarrow{V}}_M(t)$ en translation relativiste » et
Modèle:AlModèle:Transparent$\succ$le « moment d'inertie apparent $J_{\mathrm{\Delta },\text{app}}(M)={\gamma }_M(t)J_{\mathrm{\Delta }}(M)=\frac{J_{\mathrm{\Delta }}(M)}{\sqrt{1-{\left[\frac{R\bar{\mathrm{\Omega }}(t)}{c}\right]}^2}}$ $[$ou $J_{\mathrm{\Delta },\text{app}}(M)=m_{\text{app}}{R}^2]$» $\Rightarrow$ «${\sigma }_{\mathrm{\Delta },\text{relativ}}(M,t)=$ $J_{\mathrm{\Delta },\text{app}}(M)\bar{\mathrm{\Omega }}(t)$ en rotation relativiste ».