Mécanique 2 (PCSI)/Loi du moment cinétique : Moments de force

Notion de vecteur moment d’une force par rapport à un point A (ou moment vectoriel d’une force)

Définition

Modèle:Définition Modèle:AlRemarque :Le vecteur moment d'un champ vectoriel $\overrightarrow{C}(M)$ par rapport au point origine $A$ ayant été défini dans le paragraphe « vecteur moment cinétique de M par rapport au point origine A, cas particulier de vecteur moment d'un champ vectoriel défini en M par rapport au point origine A » du chap.$1$ de la leçon « Mécanique 2 (PCSI) » selon $\overrightarrow{AM}\wedge \overrightarrow{C}(M)$, on observe donc que le vecteur moment de la force $\overrightarrow{F}(M)$ appliquée au point matériel $M$ par rapport au point origine $A$ à l'instant $t$ soit ${\overrightarrow{ℳ}}_A[\overrightarrow{F}(M),t]=\overrightarrow{AM}(t)\wedge \overrightarrow{F}(M)$, est le vecteur moment du champ vectoriel $\overrightarrow{F}(M)$ par rapport au point origine $A$ et à l'instant $t$.

Propriétés

Schéma de définition du vecteur moment ${\overrightarrow{ℳ}}_A[\overrightarrow{F}(M),t]$ de la force $\overrightarrow{F}(M)$ appliquée en $M$ par rapport au point origine $A\notin$ au support de la force $\overrightarrow{F}(M)$, l'espace physique étant orienté à droite

Modèle:AlRemarquons tout d'abord que le moment vectoriel de $\overrightarrow{F}(M)$ par rapport à $A$ soit «${\overrightarrow{ℳ}}_A[\overrightarrow{F}(M),t]$» est

• nul si «$A$ est sur le support de $\overrightarrow{F}(M)$ » et
• non nul si « le support de $\overrightarrow{F}(M)$ ne passe pas par $A$», l’ensemble $\{\overrightarrow{F}(M),A\}$ formant un plan :
  Modèle:Al${\overrightarrow{ℳ}}_A[\overrightarrow{F}(M),t]$ est $\succ$de direction $\perp$ au plan $\{\overrightarrow{F}(M),A\}$ et
  Modèle:Al$\succ$de sens tel que le trièdre «$\{\overrightarrow{AM}(t),\overrightarrow{F}(M),{\overrightarrow{ℳ}}_A[\overrightarrow{F}(M),t]\}$» soit « direct si l'espace physique est orienté à droite » $($voir schéma ci-contre, sauf avis contraire, ce sera toujours le cas envisagé$)$ ou
  Modèle:AlModèle:Transparent« indirect $($au sens de la physique$)$ si l'espace physique est orienté à gauche $($cas pratiquement jamais envisagé$)$» ;
  Modèle:Alon peut aisément déterminer la direction ainsi que le sens du vecteur moment ${\overrightarrow{ℳ}}_A[\overrightarrow{F}(M),t]$ de la force $\overrightarrow{F}(M)$ par rapport à $A$, il suffit alors de spécifier sa norme pour le connaître, celle-ci se déterminant par «$\Vert {\overrightarrow{ℳ}}_A[\overrightarrow{F}(M),t]\Vert =\Vert \overrightarrow{AM}(t)\Vert \Vert \overrightarrow{F}(M)\Vert |\sin \left[\widehat{\overrightarrow{AM}(t),\overrightarrow{F}(M)}\right]|=$ $\Vert \overrightarrow{F}(M)\Vert \{\Vert \overrightarrow{AM}(t)\Vert |\sin \left(\alpha \right)|\}=\Vert \overrightarrow{F}(M)\Vert 𝖽(t)$» dans laquelle
  Modèle:Nobr représente la distance orthogonale entre le support de $\overrightarrow{F}(M)$ à l'instant $t$ et le point origine $A$ de définition du moment vectoriel »,
  grandeur qui sera appelée « bras de levier de la force Modèle:Nobr relativement à $\underset{\_}{A}$».

Changement d’origine de calcul du moment vectoriel d’une force

Modèle:AlLe « vecteur moment de la force

$\overrightarrow{F}(M)$

appliquée au point matériel

$M$

par rapport au point origine

$A$

à l'instant

$t$

» étant le « vecteur moment du champ vectoriel

$\overrightarrow{F}(M)$

par rapport à

$A$

à l'instant Modèle:Nobr on peut lui appliquer la « formule de changement d'origine du calcul de vecteur moment d'un champ vectoriel » énoncée au chap.

$1$

de la leçon « Mécanique 2 (PCSI) » et rappelée ci-dessous

«$\mathrm{\forall }(O,O^{\prime })\in {ℰ}^2,{\overrightarrow{ℳ}}_{O^{\prime }}[\overrightarrow{C}(M)]={\overrightarrow{ℳ}}_O[\overrightarrow{C}(M)]+\overrightarrow{O^{\prime }O}\wedge \overrightarrow{C}(M)$»,
soit, avec un vecteur champ $\overrightarrow{C}(M)$ s'identifiant à la force $\overrightarrow{F}(M)$,
«$\mathrm{\forall }(O,O^{\prime })\in {ℰ}^2,{\overrightarrow{ℳ}}_{O^{\prime }}[\overrightarrow{F}(M),t]={\overrightarrow{ℳ}}_O[\overrightarrow{F}(M),t]+\overrightarrow{O^{\prime }O}\wedge \overrightarrow{F}(M)$».

Définition du moment (scalaire) d’une force par rapport à un axe Δ, bras de levier de la force

Équiprojectivité du « moment vectoriel d'une force »

Modèle:AlCette notion introduite pour un champ de vecteurs

$\overrightarrow{f}(M)$

dans le paragraphe « définition de l'équiprojectivité d'un champ de vecteurs d'un espace affine euclidien tridimensionnel

$ℰ$

» du chap.

$1$

de la leçon « Outils mathématiques pour la physique - bis (PCSI) » à savoir

«$\mathrm{\forall }(M,N)\in {ℰ}^2,\overrightarrow{f}(M)\cdot \overrightarrow{MN}=\overrightarrow{f}(N)\cdot \overrightarrow{MN}$»,

Modèle:Aln'est pas vérifiée pour n'importe quel champ de vecteurs mais $\dots$

Modèle:All'est pour un champ de vecteurs moment d'un champ vectoriel quelconque

$\overrightarrow{C}(M)$

défini par «

$\mathrm{\forall }P\in ℰ$

,

${\overrightarrow{ℳ}}_P[\overrightarrow{C}(M)]=\overrightarrow{PM}\wedge \overrightarrow{C}(M)$

»

$[$

voir le paragraphe « notion d'équiprojectivité du champ de vecteurs moment d'un champ vectoriel » du chap.

$1$

de la leçon « Mécanique 2 (PCSI) »

$]$

c'est-à-dire

«$\mathrm{\forall }(P,Q)\in {ℰ}^2,{\overrightarrow{ℳ}}_P[\overrightarrow{C}(M)]\cdot \overrightarrow{PQ}={\overrightarrow{ℳ}}_Q[\overrightarrow{C}(M)]\cdot \overrightarrow{PQ}\mathrm{\forall }\overrightarrow{C}(M)$».

Modèle:AlLe « vecteur moment de la force

$\overrightarrow{F}(M)$

appliquée au point matériel

$M$

par rapport au point origine

$A$

à l'instant

$t$

» étant le « vecteur moment du champ vectoriel

$\overrightarrow{F}(M)$

par rapport à

$A$

à l'instant Modèle:Nobr on peut lui appliquer la propriété d'équiprojectivité rappelée ci-dessus soit

«$\mathrm{\forall }(A,A^{\prime })\in {ℰ}^2,{\overrightarrow{ℳ}}_A[\overrightarrow{F}(M),t]\cdot \overrightarrow{A{A}^{\prime }}={\overrightarrow{ℳ}}_{A^{\prime }}[\overrightarrow{F}(M),t]\cdot \overrightarrow{A{A}^{\prime }}$».

Modèle:AlRemarque : en utilisant la notion $($hors programme de physique de P.C.S.I.$)$ de « torseur » introduite dans le chap.$1$ de la leçon « Outils mathématiques pour la physique - bis (PCSI) », le moment $($vectoriel$)$ Modèle:Nobr de la force $\overrightarrow{F}(M)$ appliquée au point matériel $M$ par rapport à $A$ à l'instant $t$ étant le moment du torseur (glisseur) statique de résultante $\overrightarrow{F}(M)$ à savoir «${𝒯}_{\text{stat}}$» d'éléments de réduction en $A$ «${𝒯}_{\text{stat}}=$ ${\left\{\begin{array}{c}\overrightarrow{F}(M)\\ {\overrightarrow{ℳ}}_A[\overrightarrow{F}(M),t]=\overrightarrow{AM}(t)\wedge \overrightarrow{F}(M)\end{array}\right\}}_A$» et
Modèle:AlModèle:Transparentle « moment d'un torseur au point $A$» étant par définition un « champ de vecteurs équiprojectif » nous en déduisons, sans autre développement, le caractère « équiprojectif » du « vecteur moment de la force $\overrightarrow{F}(M)$ appliquée au point matériel $M$ par rapport au point origine $A$ à l'instant $t$».

Définition du moment scalaire d'une force par rapport à un axe Δ

Modèle:AlConsidérant un axe

$\mathrm{\Delta }$

quelconque et deux points quelconques

$($

distincts

$)$

de cet axe

$(A,A^{\prime }\ne A)\in {\mathrm{\Delta }}^2$

, nous déduisons de l'équiprojectivité du vecteur moment de la force

$\overrightarrow{F}(M)$

appliquée au point matériel

$M$

à l'instant

$t$

la relation

«${\overrightarrow{ℳ}}_A[\overrightarrow{F}(M),t]\cdot \overrightarrow{A{A}^{\prime }}={\overrightarrow{ℳ}}_{A^{\prime }}[\overrightarrow{F}(M),t]\cdot \overrightarrow{A{A}^{\prime }}$»
soit, en orientant l'axe $\mathrm{\Delta }$ par ${\overrightarrow{u}}_{\mathrm{\Delta }}$ $\Rightarrow$ $\overrightarrow{A{A}^{\prime }}=\overline{A{A}^{\prime }}{\overrightarrow{u}}_{\mathrm{\Delta }}$ et en simplifiant par $\overline{A{A}^{\prime }}\ne 0$,
«${\overrightarrow{ℳ}}_A[\overrightarrow{F}(M),t]\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}={\overrightarrow{ℳ}}_{A^{\prime }}[\overrightarrow{F}(M),t]\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}$»,

Modèle:Alcette valeur constante sur

$\mathrm{\Delta }$

définissant le moment

$($

scalaire

$)$

de la force

$\overrightarrow{F}(M)$

appliquée au point matériel

$M$

par rapport à l'axe

$\mathrm{\Delta }$

à l'instant

$t$

.

1^ère méthode de détermination du moment scalaire d'une force par rapport à un axe Δ

Modèle:AlPour exprimer le moment scalaire d’une force $\overrightarrow{F}(M)$ appliquée au point matériel $M$ par rapport à un axe $\mathrm{\Delta }$ orienté par ${\overrightarrow{u}}_{\mathrm{\Delta }}$, on peut

• déterminer les composantes de son moment vectoriel en un point $A\in \mathrm{\Delta }$ dans une base orthonormée « directe si l'espace est orienté à droite » $($pratiquement toujours le cas considéré$)$ ou
  Modèle:Transparent« indirecte $($au sens de la physique$)$ si l'espace est orienté à gauche » $($cas pratiquement jamais envisagé$)$ et
• multiplier scalairement par ${\overrightarrow{u}}_{\mathrm{\Delta }}$ pour obtenir le moment scalaire cherché.

2^ème méthode de détermination du moment scalaire d'une force par rapport à un axe Δ, notion de bras de levier de la force relativement à l'axe

Modèle:AlMéthode à préférer car c'est, en général et de très loin, la plus rapide.

Modèle:AlPréliminaire : De «${ℳ}_{\mathrm{\Delta }}[\overrightarrow{F}(M),t]=[\overrightarrow{AM}(t)\wedge \overrightarrow{F}(M)]\cdot {\overrightarrow{u}}_{\mathrm{\Delta }},\mathrm{\forall }A\in \mathrm{\Delta }$», produit mixte des trois vecteurs «$\{\overrightarrow{AM}(t),\overrightarrow{F}(M),{\overrightarrow{u}}_{\mathrm{\Delta }}\}$», on en déduit que ce dernier est nul si ces trois vecteurs sont coplanaires ;
Modèle:AlModèle:Transparentor «$A\in \mathrm{\Delta }$» alors que «$M$ a priori $\notin \mathrm{\Delta }$» $\Rightarrow$ «$\overrightarrow{AM}(t)$ et ${\overrightarrow{u}}_{\mathrm{\Delta }}$ ne sont pas colinéaires et forment un plan » ;
Modèle:AlModèle:Transparenton a donc deux cas de figures suivant que $\overrightarrow{F}(M)$ appartient ou n'appartient pas à ce plan :

Schéma en perspective de définition du moment scalaire d'une force par rapport à un axe, le support de la force appliquée en un point extérieur à l'axe coupant ce dernier

Schéma en perspective de définition du moment scalaire d'une force par rapport à un axe, le support de la force appliquée en un point extérieur à l'axe ne coupant pas ce dernier

Modèle:AlCi-contre à gauche le cas de figure dans lequel la force $\overrightarrow{F}(M)$ appliquée au point matériel $M$ appartient au plan $\{\overrightarrow{AM}(t),{\overrightarrow{u}}_{\mathrm{\Delta }}\}$, les trois vecteurs $\overrightarrow{F}(M)$, $\overrightarrow{AM}(t)$ et ${\overrightarrow{u}}_{\mathrm{\Delta }}$ étant coplanaires le moment scalaire de $\overrightarrow{F}(M)$ par rapport à $\mathrm{\Delta }$ est nul soit mathématiquement Modèle:Nobr

Modèle:AlCi-contre à droite le cas de figure dans lequel la force $\overrightarrow{F}(M)$ appliquée au point matériel $M$ n'appartient pas au plan $\{\overrightarrow{AM}(t),{\overrightarrow{u}}_{\mathrm{\Delta }}\}$, les trois vecteurs $\overrightarrow{F}(M)$, $\overrightarrow{AM}(t)$ et ${\overrightarrow{u}}_{\mathrm{\Delta }}$ n'étant pas coplanaires le moment scalaire de $\overrightarrow{F}(M)$ par rapport à $\mathrm{\Delta }$ est non nul soit mathématiquement «${ℳ}_{\mathrm{\Delta }}[\overrightarrow{F}(M),t]\ne 0$» ;
Modèle:AlModèle:Transparentdécomposant la force $\overrightarrow{F}(M)$ en une composante $\parallel$ à $\mathrm{\Delta }$ «${\overrightarrow{F}}_{\parallel }$» et une composante $\perp$ à $\mathrm{\Delta }$ «${\overrightarrow{F}}_{\perp }$» soit «$\overrightarrow{F}(M)=$ ${\overrightarrow{F}}_{\parallel }(M)+{\overrightarrow{F}}_{\perp }(M)$», on déduit de la distributivité de la multiplication vectorielle et de la multiplication scalaire relativement à l'addition vectorielle $(\Rightarrow$ celle de la multiplication mixte par rapport à l'addition vectorielle$)$ «${ℳ}_{\mathrm{\Delta }}[\overrightarrow{F}(M),t]=\cancel{{ℳ}_{\mathrm{\Delta }}[{\overrightarrow{F}}_{\parallel }(M),t]+}{ℳ}_{\mathrm{\Delta }}[{\overrightarrow{F}}_{\perp }(M),t]$», le 1^er terme du 2^ème membre étant nul ; il reste donc à évaluer ${ℳ}_{\mathrm{\Delta }}[{\overrightarrow{F}}_{\perp }(M),t]$ $[$schéma ci-dessous à droite$]$ :

Schéma en vue de dessus de définition du moment scalaire d'une force par rapport à un axe, le support de la composante de la force sur le plan perpendiculaire à l'axe appliquée en un point extérieur à l'axe ne passant pas par la trace de ce dernier sur le plan

Modèle:AlModèle:Transparent$\succ$tout d'abord on cherche le signe du moment scalaire $[$le sens «$+$» de rotation dans le plan $\perp$ à l’axe $\mathrm{\Delta }$ et passant par $M$ Modèle:Nobr le plan de la figure ci-contre$)$ étant défini par le sens de ${\overrightarrow{u}}_{\mathrm{\Delta }}$ $($sur l'exemple ci-contre sens trigonométrique direct$\left)\right]$ :

• si ${\overrightarrow{F}}_{\perp }(M)$ tend à faire tourner $M$ dans le sens «$+$» le moment scalaire est $>0$ et
• si ${\overrightarrow{F}}_{\perp }(M)$ tend à faire tourner $M$ dans le sens «$-$» le moment scalaire est $<0$,
  Modèle:Ald'où, dans l’exemple ci-contre, «${ℳ}_{\mathrm{\Delta }}[{\overrightarrow{F}}_{\perp }(M),t]<0$»,

Modèle:AlModèle:Transparent$\succ$ensuite on détermine la valeur absolue du moment scalaire par «$\left|{ℳ}_{\mathrm{\Delta }}[{\overrightarrow{F}}_{\perp }(M),t]\right|=\Vert {\overrightarrow{F}}_{\perp }(M)\Vert 𝖽(t)$» où Modèle:Nobr est le bras de levier, à l'instant $t$, de ${\overrightarrow{F}}_{\perp }(M)$ relativement à $\mathrm{\Delta }$» c'est-à-dire la « distance orthogonale entre le support de ${\overrightarrow{𝐅}}_{\mathbf{\perp }}\mathbf{(}𝐌\mathbf{)}$ et l’axe »,

Modèle:AlModèle:Transparent$\succ$enfin on en déduit la valeur de «${ℳ}_{\mathrm{\Delta }}[{\overrightarrow{F}}_{\perp }(M),t]$» :

• si ${\overrightarrow{F}}_{\perp }(M)$ tend à faire tourner $M$ dans le sens «$+$», «${ℳ}_{\mathrm{\Delta }}[{\overrightarrow{F}}_{\perp }(M),t]=+\Vert {\overrightarrow{F}}_{\perp }(M)\Vert 𝖽(t)$» et
• si ${\overrightarrow{F}}_{\perp }(M)$ tend à faire tourner $M$ dans le sens «$-$», «${ℳ}_{\mathrm{\Delta }}[{\overrightarrow{F}}_{\perp }(M),t]=-\Vert {\overrightarrow{F}}_{\perp }(M)\Vert 𝖽(t)$» $[$cas de figure ci-contre$]$.

Modèle:AlConclusion : Si « le support de la force $\overrightarrow{F}(M)$ coupe $($au sens large$)$ l’axe $\mathrm{\Delta }$ de définition du moment scalaire de la force $\overrightarrow{F}(M)$ », ce dernier est nul Modèle:Nobr

Modèle:AlModèle:Transparentsi « le support de la force $\overrightarrow{F}(M)$ et l’axe $\mathrm{\Delta }$ de définition du moment scalaire de cette dernière ne sont pas coplanaires », ce dernier est non nul Modèle:Nobr et est égal au moment scalaire de la composante ${\overrightarrow{F}}_{\perp }(M)$ de la force $\overrightarrow{F}(M)$ sur le plan passant par $M$ et $\perp$ à l’axe, soit

Modèle:AlModèle:Transparent$\succ$si ${\overrightarrow{F}}_{\perp }(M)$ tend à faire tourner $M$ dans le sens «$+$», «${ℳ}_{\mathrm{\Delta }}[\overrightarrow{F}(M),t]={ℳ}_{\mathrm{\Delta }}[{\overrightarrow{F}}_{\perp }(M),t]=+\Vert {\overrightarrow{F}}_{\perp }(M)\Vert 𝖽(t)$» et

Modèle:AlModèle:Transparent$\succ$si ${\overrightarrow{F}}_{\perp }(M)$ tend à faire tourner $M$ dans le sens «$-$», «${ℳ}_{\mathrm{\Delta }}[\overrightarrow{F}(M),t]={ℳ}_{\mathrm{\Delta }}[{\overrightarrow{F}}_{\perp }(M),t]=-\Vert {\overrightarrow{F}}_{\perp }(M)\Vert 𝖽(t)$»,

Modèle:AlModèle:Transparent«$𝖽(t)$ étant le bras de levier, à l'instant $t$, de ${\overrightarrow{F}}_{\perp }(M)$ relativement à $\mathrm{\Delta }$» dans les deux cas.

Exemples de calcul de moment scalaire de force : moment scalaire de la tension de la tige idéale rigide et moment scalaire du poids dans l’exemple du pendule pesant simple (P.P.S.) à un degré de liberté

Modèle:AlPréliminaire : Il est toujours préférable de faire des schémas de situation avec des « paramètres de position positifs » de façon à raisonner sur le schéma sans avoir à « tenir compte du signe du Modèle:Nobr

Modèle:AlModèle:Transparentnous nous proposons de déterminer le moment scalaire du poids dans l'exemple du P.P.S. à un degré de liberté $[$le P.P.S. étant écarté de ${\theta }_0$ de sa position d’équilibre stable et lâché sans vitesse initiale, le point matériel $M$ décrit alors un mouvement circulaire de rayon $𝑙$ d'axe $\mathrm{\Delta }\perp$ au plan vertical de lancement$]$ en faisant deux schémas de situation avec un changement de signe du paramètre de position pour y souligner l'intérêt de faire un schéma avec une abscisse angulaire de $M$ à l'instant $t$ positive $\dots$

Schéma représentant un pendule pesant simple $($P.P.S.$)$ à un degré de liberté ainsi que les deux forces agissant sur M à un instant où le paramètre de position est positif

Schéma représentant un pendule pesant simple $($P.P.S.$)$ à un degré de liberté ainsi que les deux forces agissant sur M à un instant où le paramètre de position est négatif

Modèle:AlModèle:TransparentCi-contre à gauche schéma représentant un P.P.S. à un degré de liberté ainsi que les deux forces agissant sur $M$ à un instant où l'abscisse angulaire $\theta$ de ce dernier est $>0$, schéma souhaitable n'induisant pas d'erreur potentielle de signe sur l'évaluation du moment scalaire du poids de $M$ «${ℳ}_{\mathrm{\Delta }}\left[m\overrightarrow{g}\right]$» si on oublie le signe de $\theta$ ;

Modèle:AlModèle:TransparentCi-contre à droite schéma représentant un P.P.S. à un degré de liberté ainsi que les deux forces agissant sur $M$ à un instant où l'abscisse angulaire $\theta$ de ce dernier est $<0$, schéma à éviter car susceptible d'induire une erreur de signe sur l'évaluation du moment scalaire du poids de $M$ «${ℳ}_{\mathrm{\Delta }}\left[m\overrightarrow{g}\right]$» si on oublie le signe de $\theta$, en effet
Modèle:AlModèle:Transparenton observe, sur ce schéma, que $m\overrightarrow{g}$ tendant à faire tourner $M$ dans le sens «$+$» $\Rightarrow$ Modèle:Nobr avec ${ℳ}_{\mathrm{\Delta }}\left[m\overrightarrow{g}\right]=\Vert m\overrightarrow{g}\Vert 𝖽$ dans laquelle le bras de levier de $m\overrightarrow{g}$ s'écrit «$𝖽=𝑙|\sin (\theta )|$»Modèle:, d'où l'erreur potentielle si on oublie le signe de $\theta$ du schéma en écrivant «$\cancel{𝖽=𝑙\sin (\theta )}$» ce qui conduit à un bras de levier $<0$ contraire à la définition d'un bras de levier
Modèle:AlModèle:Transparent$[$en fait, comme $\theta$ est $<0$ sur le schéma ci-contre à droite, on a «$|\sin (\theta )|=-\sin (\theta )$» et par suite «$𝖽=-𝑙\sin (\theta )$» $\Rightarrow$ ${ℳ}_{\mathrm{\Delta }}\left[m\overrightarrow{g}\right]=-mg𝑙\sin (\theta )>0$ conforme au signe du moment scalaire de $m\overrightarrow{g}$ observé sur le schéma, $(g$ étant l'intensité de la pesanteur c'est-à-dire $g=\Vert \overrightarrow{g}\Vert \left)\right]$.

Modèle:AlÉvaluation du moment scalaire du poids du P.P.S. relativement à l'axe

$\underset{\_}{\mathrm{\Delta }}$ $($

sur le schéma ci-contre à gauche

$)$

 : on observe, sur ce schéma, que

$m\overrightarrow{g}$

tendant à faire tourner

$M$

dans le sens «

$-$

»

$\Rightarrow$

Modèle:Nobr avec

$\left|{ℳ}_{\mathrm{\Delta }}\left[m\overrightarrow{g}\right]\right|=$ $\Vert m\overrightarrow{g}\Vert 𝖽$

dans laquelle le bras de levier de

$m\overrightarrow{g}$

s'écrit Modèle:Nobr

$=𝑙\sin (\theta )$

» car

$\theta$

, sur le schéma, est

$>0$

soit

$\left|{ℳ}_{\mathrm{\Delta }}\left[m\overrightarrow{g}\right]\right|=\Vert m\overrightarrow{g}\Vert 𝑙\sin (\theta )$

et, en posant

$g=\Vert \overrightarrow{g}\Vert$

,

«${ℳ}_{\mathrm{\Delta }}[m\overrightarrow{g},t]=-mg𝑙\sin [\theta (t)]$».

Modèle:AlÉvaluation du moment scalaire de la tension de la tige idéale rigide du P.P.S. relativement à l'axe

$\underset{\_}{\mathrm{\Delta }}$ $($

sur le schéma ci-dessus à gauche

$)$

 : le support de la tension

$\overrightarrow{T}(t)$

de la tige idéale rigide coupant l’axe

$\mathrm{\Delta }$

, son moment scalaire par rapport à cet axe est nul soit

«${ℳ}_{\mathrm{\Delta }}[\overrightarrow{T}(t)]=0$»Modèle:,.

Distinction entre forces extérieures et intérieures appliquées à un système discret fermé de points matériels, généralisation à un système continu fermé de matière

Distinction entre forces extérieures et intérieures appliquées à un système discret fermé de points matériels

Modèle:AlLa distinction entre forces extérieures et intérieures appliquées à un système discret fermé de points matériels ${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$ dans lequel Modèle:Nobr introduite au paragraphe « système des forces extérieures et système des forces intérieures s'exerçant sur un système de points matériels fermé » du chap.$6$ de la leçon « Mécanique 1 (PCSI) » est rappelée ci-dessous :

• le système des forces extérieures appliquées au système discret fermé de points matériels ${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$ est l'ensemble des forces ${\left\{{\overrightarrow{F}}_{i\leftarrow \left\{{\text{ext}}_k\right\}}\right\}}_{i\in \left[[1,N]\right]}$ que chaque système $\left({\mathrm{\Sigma }}_k\right)$ extérieur au système de points matériels ${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$ exerce sur chaque point matériel $M_i$ de ce dernier ;
• le système des forces intérieures agissant dans le système discret fermé de points matériels ${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$ est l'ensemble des forces ${\left\{{\overrightarrow{F}}_{i\leftarrow j}\right\}}_{(i,j\ne i)\in {\left[[1,N]\right]}^2}$ que chaque point matériel $M_j$ du système de points matériels ${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$ exerce sur chaque point matériel $M_i$ de ce dernier.

Généralisation à un système continu fermé de matière d'expansion tridimensionnelle

Modèle:AlIl existe deux types principaux de forces s'exerçant sur un système continu de matière d'expansion tridimensionnelle qui seront vus plus en détail aux paragraphes « champs de forces volumique ou surfacique dans un fluide, exemples », « champ de force volumique et sa densité volumique de force, retour sur les exemples » et « champ de force surfacique et sa densité surfacique de force, cas de la densité surfacique de force pressante » du chap.$1$ de la leçon « Statique des fluides (PCSI) » :

• les forces volumiques $($forces de champ$)$ s’exerçant sur tous les pseudo-points de l'expansion tridimensionnelle $\left(𝒱\right)$, forces volumiques notées $d{\overrightarrow{F}}_V(M)={\overrightarrow{f}}_V(M)d{𝒱}_M$ avec ${\overrightarrow{f}}_V(M)$ densité volumique de force de champ au point $M$ et
• les forces surfaciques $($forces de contact$)$ s'exerçant sur chaque surface élémentaire de la surface fermée limitant un pseudo-point, forces surfaciques notées $d^2{\overrightarrow{F}}_S(N_M)=$ Modèle:Nobr avec ${\overrightarrow{f}}_S(N_M)$ densité surfacique de force de contact au point $N_M$ $[N_M$ désignant un point de la surface fermée limitant le pseudo-point centré en $M$$]$.

Modèle:AlOn fait également la distinction entre forces extérieures et intérieures appliquées à un système continu fermé de matière d'expansion tridimensionnelle $\left(𝒱\right)$ en prolongeant celle faite dans le paragraphe « distinction entre forces extérieures et intérieures appliquées à un système discret fermé de points matériels » ci-dessus selon :

• les forces extérieures appliquées au système continu fermé de matière d'expansion tridimensionnelle $\left(𝒱\right)$, lesquelles sont des deux types principaux de forces rappelés ci-dessus à savoir
  $\succ$des forces volumiques $($c'est-à-dire de champ$)$ $d{\overrightarrow{F}}_{V,\{M,d{𝒱}_M\}\leftarrow {\text{ext}}_k}(M)={\overrightarrow{f}}_{V,M\leftarrow {\text{ext}}_k}(M)d{𝒱}_M$ que l'extérieur du système exerce sur chaque pseudo-point centré en $M\in \left(𝒱\right)$ ou
  $\succ$des forces surfaciques $($c'est-à-dire de contact$)$ $d^2{\overrightarrow{F}}_{S,\{N,d^2{S}_N\}\leftarrow {\text{ext}}_l}(N)={\overrightarrow{f}}_{S,N\leftarrow {\text{ext}}_l}(N)d^2{S}_N$ que l'extérieur du système exerce sur chaque point $N$ de la surface fermée limitant $\left(𝒱\right)$ ;
• les forces intérieures agissant dans le système continu fermé de matière d'expansion tridimensionnelle $\left(𝒱\right)$ limitée par la surface fermée $\left(S\right)$ sont
  $\succ$des forces de champ s'exerçant entre deux pseudo-points du système $($elles sont d'un autre type que les deux types principaux de forces rappelés ci-dessus, on pourrait les qualifier de « bivolumiques »$)$ à savoir $d^2{\overrightarrow{F}}_{\{M,d{𝒱}_M\}\leftarrow \{M^{\prime },d{𝒱}_{M^{\prime }}\}}(M)$ force que le pseudo-point centré en $M^{\prime }$ exerce sur le pseudo-point centré en $M$ $\{$le rapport ${\overrightarrow{f}}_{\text{bivol},M\leftarrow M^{\prime }}(M)=$ $\frac{d^2{\overrightarrow{F}}_{\{M,d{𝒱}_M\}\leftarrow \{M^{\prime },d{𝒱}_{M^{\prime }}\}}(M)}{d{𝒱}_{M}d{𝒱}_{M^{\prime }}}$ pourrait être appelé densité bivolumique de force que $M^{\prime }$ exerce sur $M\}$ ou
  $\succ$des forces de contact entre deux pseudo-points voisins $d^2{\overrightarrow{F}}_{S,\{N,d^2{S}_N\}\leftarrow \{N_{\text{voisin}},d^2{S}_N\}}(N)$ $={\overrightarrow{f}}_{S,N\leftarrow N_{\text{voisin}}}(N)d^2{S}_N$.

Modèle:AlRemarque 1 : Dans le cas où le système continu de matière devient d'expansion surfacique $\left(𝒮\right)$ parce qu'une des dimensions de l'expansion volumique initiale est infiniment petite,
Modèle:AlModèle:Transparentles forces volumiques de champ initiales sont à remplacer par des forces surfaciques de champ s'exerçant sur tous les pseudo-points de l'expansion surfacique $\left(𝒮\right)$ notées $d{\overrightarrow{F}}_S(M)=$ ${\overrightarrow{f}}_S(M)d{𝒮}_M$ avec ${\overrightarrow{f}}_S(M)$ densité surfacique de force de champ au point $M$ et
Modèle:AlModèle:Transparentles forces surfaciques de contact initiales Modèle:Transparent par des forces linéiques de contact s'exerçant sur chaque longueur élémentaire de la courbe fermée limitant un pseudo-point, notées $d^2{\overrightarrow{F}}_{𝑙}(N_M)={\overrightarrow{f}}_{𝑙}(N_M)d^2{𝑙}_{N_M}$ avec ${\overrightarrow{f}}_{𝑙}(N_M)$ densité linéique de force de contact au point $N_M$ $[N_M$ désignant un point de la courbe fermée limitant le pseudo-point centré en $M$$]$ ;

Modèle:AlModèle:Transparenton distingue : les forces extérieures appliquées au système continu fermé d'expansion surfacique $\left(𝒮\right)$, lesquelles sont des deux types principaux de forces rappelés ci-dessus à savoir
$\succ$des forces surfaciques $($c'est-à-dire de champ$)$ $d{\overrightarrow{F}}_{S,\{M,d{𝒮}_M\}\leftarrow {\text{ext}}_k}(M)={\overrightarrow{f}}_{S,M\leftarrow {\text{ext}}_k}(M)d{𝒮}_M$ que l'extérieur du système exerce sur chaque pseudo-point centré en $M\in \left(𝒮\right)$ ou
$\succ$des forces linéiques $($c'est-à-dire de contact$)$ $d^2{\overrightarrow{F}}_{𝑙,\{N,d^2{𝑙}_N\}\leftarrow {\text{ext}}_l}(N)={\overrightarrow{f}}_{𝑙,N\leftarrow {\text{ext}}_l}(N)d^2{𝑙}_N$ que l'extérieur du système exerce sur chaque point $N$ de la courbe fermée limitant $\left(𝒮\right)$ ;

Modèle:AlModèle:Transparentles forces intérieures agissant dans le système continu fermé d'expansion surfacique $\left(𝒮\right)$ limitée par la courbe fermée $\left(C\right)$ sont des forces de champ s'exerçant entre deux pseudo-points du système $($sont d'un autre type que les deux types principaux de forces rappelés ci-dessus, on pourrait les qualifier de « bisurfaciques »$)$ à savoir $d^2{\overrightarrow{F}}_{\{M,d{𝒮}_M\}\leftarrow \{M^{\prime },d{𝒮}_{M^{\prime }}\}}(M)$ force que le pseudo-point centré en $M^{\prime }$ exerce sur le pseudo-point centré en $M$ $\{$le rapport ${\overrightarrow{f}}_{\text{bisurf},M\leftarrow M^{\prime }}(M)=\frac{d^2{\overrightarrow{F}}_{\{M,d{𝒮}_M\}\leftarrow \{M^{\prime },d{𝒮}_{M^{\prime }}\}}(M)}{d{𝒮}_{M}d{𝒮}_{M^{\prime }}}$ pourrait être appelé densité bisurfacique de force que $M^{\prime }$ exerce sur $M\}$ ou des forces de contact entre pseudo-points voisins $d^2{\overrightarrow{F}}_{S,\{N,d^2{𝑙}_N\}\leftarrow \{N_{\text{voisin}},d^2{𝑙}_N\}}(N)=$ ${\overrightarrow{f}}_{S,N\leftarrow N_{\text{voisin}}}(N)d^2{𝑙}_N$.

Modèle:AlRemarque 2 : Dans le cas où le système continu de matière devient d'expansion linéique $\left(\mathrm{\Gamma }\right)$ parce que deux des dimensions de l'expansion volumique initiale sont infiniment petites,
Modèle:AlModèle:Transparentles forces volumiques de champ initiales sont à remplacer par des forces linéiques de champ s'exerçant sur tous les pseudo-points de l'expansion linéique $\left(\mathrm{\Gamma }\right)$ notées $d{\overrightarrow{F}}_{𝑙}(M)=$ ${\overrightarrow{f}}_{𝑙}(M)d{𝑙}_M$ avec ${\overrightarrow{f}}_{𝑙}(M)$ densité linéique de force de champ au point $M$ et
Modèle:AlModèle:Transparentles forces surfaciques de contact initiales Modèle:Transparent par des forces de contact s'exerçant entre chaque pseudo-point voisin, notées ${\overrightarrow{f}}_{M\leftarrow M_g}(M)$ ou ${\overrightarrow{f}}_{M\leftarrow M_d}(M)$ suivant que le pseudo-point voisin du pseudo-point centré en $M$ est situé d'un côté ou de l'autre ou
Modèle:AlModèle:Transparent exercées sur l'un ou l'autre des pseudo-points extrêmes limitant l'expansion linéique $\left(\mathrm{\Gamma }\right)$ ;

Modèle:AlModèle:Transparenton distingue : les forces extérieures appliquées au système continu fermé d'expansion linéique $\left(\mathrm{\Gamma }\right)$, lesquelles sont des deux types principaux de forces rappelés ci-dessus à savoir
$\succ$des forces linéiques $($c'est-à-dire de champ$)$ $d{\overrightarrow{F}}_{𝑙,\{M,d{𝓁}_M\}\leftarrow {\text{ext}}_k}(M)={\overrightarrow{f}}_{𝑙,M\leftarrow {\text{ext}}_k}(M)d{𝓁}_M$ que l'extérieur du système exerce sur chaque pseudo-point centré en $M\in \left(\mathrm{\Gamma }\right)$ ou
$\succ$les forces de contact exercées sur les pseudo-points extrêmes limitant l'expansion linéique $\left(\mathrm{\Gamma }\right)$, ${\overrightarrow{f}}_{N_g\leftarrow {\text{ext}}_l}(N_g)$ ou ${\overrightarrow{f}}_{N_d\leftarrow {\text{ext}}_{l^{\prime }}}(N_d)$ que l'extérieur du système exerce sur chaque point extrême limitant $\left(\mathrm{\Gamma }\right)$ suivant le côté considéré ;

Modèle:AlModèle:Transparentles forces intérieures agissant dans le système continu fermé d'expansion linéique $\left(\mathrm{\Gamma }\right)$ sont des forces de champ s'exerçant entre deux pseudo-points du système $($sont d'un autre type que les deux types principaux de forces rappelés ci-dessus, on pourrait les qualifier de « bilinéiques »$)$ à savoir $d^2{\overrightarrow{F}}_{\{M,d{𝑙}_M\}\leftarrow \{M^{\prime },d{𝑙}_{M^{\prime }}\}}(M)$ force que le pseudo-point centré en $M^{\prime }$ exerce sur le pseudo-point centré en $M$ $\{$le rapport ${\overrightarrow{f}}_{\text{bilin},M\leftarrow M^{\prime }}(M)=\frac{d^2{\overrightarrow{F}}_{\{M,d{𝑙}_M\}\leftarrow \{M^{\prime },d{𝑙}_{M^{\prime }}\}}(M)}{d{𝑙}_{M}d{𝑙}_{M^{\prime }}}$ pourrait être appelé densité bilinéique de force que $M^{\prime }$ exerce sur $M\}$ ou des forces de contact entre pseudo-points voisins ${\overrightarrow{f}}_{M\leftarrow M_g}(M)$ ou ${\overrightarrow{f}}_{M\leftarrow M_d}(M)$ suivant que le pseudo-point voisin du pseudo-point centré en $M$ est situé d'un côté ou de l'autre.

Conséquence du principe des actions réciproques sur le système des forces intérieures

Modèle:AlLe principe des actions réciproques $($ou 3^ème loi de Newton$)$ a déjà été énoncé et commenté au paragraphe « énoncé du principe des actions réciproques et commentaires » du chap.$6$ de la leçon « Mécanique 1 (PCSI) », il ne s'agit donc que d'un rappel dans les deux 1^ers sous-paragraphes ci-dessous.

Rappel : résultante des forces intérieures s’exerçant sur un système discret fermé de points matériels

Modèle:AlLa résultante des forces intérieures

${\overrightarrow{F}}_{\text{int}}$

s’exerçant sur le système discret fermé de points matériels

${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$

avec Modèle:Nobr étant définie selon «

${\overrightarrow{F}}_{\text{int}}=\sum _{i=1..N}\left[\sum _{j=1..N}^{j\ne i}{\overrightarrow{F}}_{i\leftarrow j}\right]$ $=\sum _{i=1..N}\left[\sum _{j=1..i-1}^{j=i+1..N}{\overrightarrow{F}}_{i\leftarrow j}\right]$

», on déduit du principe des actions réciproques en dynamique newtonienne « la nullité de la résultante des forces intérieures s’exerçant sur un système de points matériels fermé en dynamique newtonienne »

$($

on établit de la même façon que la propriété reste applicable en dynamique relativiste

$)$

soit

«${\overrightarrow{F}}_{\text{int}}=\overrightarrow{0}$».

Généralisation : résultante des forces intérieures s’exerçant sur un système continu fermé de matière

Modèle:AlLa résultante des forces intérieures

${\overrightarrow{F}}_{\text{int}}$

s’exerçant sur le système continu fermé de matière d'expansion tridimensionnelle

$\left(𝒱\right)$

étant définie selon «

${\overrightarrow{F}}_{\text{int}}={\overrightarrow{F}}_{\text{int. de champ}}+{\overrightarrow{F}}_{\text{int. de contact}}$

» avec Modèle:Nobr

$=\iiint \underset{(M,M^{\prime })\in {\left(𝒱\right)}^2}{\iiint }{d}^2{\overrightarrow{F}}_{\{M,d{𝒱}_M\}\leftarrow \{M^{\prime },d{𝒱}_{M^{\prime }}\}}(M)$

»Modèle:, et «

${\overrightarrow{F}}_{\text{int. de contact}}=$ $\underset{M\in \left(𝒱\right)}{\iiint }[\underset{N_M\in d{S}_M}{\text{∯}}{d}^2{\overrightarrow{F}}_{S,\{N_M,d^2{S}_N\}\leftarrow \{N_{\text{voisin de }{N}_M},d^2{S}_N\}}(N_M)]$

»Modèle:,, on déduit du principe des actions réciproques en dynamique newtonienne Modèle:Nobr dans chaque résultante partielle

${\overrightarrow{F}}_{\text{int. de champ}}$

et

${\overrightarrow{F}}_{\text{int. de contact}}$

en regroupant les termes par couples

$)$

la nullité de chaque résultante partielle et par suite « la nullité de la résultante des forces intérieures s’exerçant sur un système continu fermé d'expansion tridimensionnelle en dynamique newtonienne »

$($

on établit de la même façon que la propriété reste applicable en dynamique relativiste

$)$

soit

«${\overrightarrow{F}}_{\text{int}}=\overrightarrow{0}$».

Modèle:AlRemarques : Ce qui vient d'être établi pour un système continu fermé de matière d'expansion tridimensionnelle est encore applicable pour un système continu fermé de matière d'expansion surfacique ou linéique, les seules modifications portant sur le type d'intégrales y intervenant :

Modèle:AlModèle:TransparentLa résultante des forces intérieures

${\overrightarrow{F}}_{\text{int}}$

s’exerçant sur le système continu fermé de matière d'expansion surfacique

$\left(𝒮\right)$

étant définie selon «

${\overrightarrow{F}}_{\text{int}}={\overrightarrow{F}}_{\text{int. de champ}}+{\overrightarrow{F}}_{\text{int. de contact}}$

» avec Modèle:Nobr

$=\iint \underset{(M,M^{\prime })\in {\left(𝒮\right)}^2}{\iint }{d}^2{\overrightarrow{F}}_{\{M,d{𝒮}_M\}\leftarrow \{M^{\prime },d{𝒮}_{M^{\prime }}\}}(M)$

»Modèle:, et «

${\overrightarrow{F}}_{\text{int. de contact}}=$ $\underset{M\in \left(𝒮\right)}{\iint }[\underset{N_M\in d{𝑙}_M}{\oint }{d}^2{\overrightarrow{F}}_{𝑙,\{N_M,d^2{𝑙}_N\}\leftarrow \{N_{\text{voisin de }{N}_M},d^2{𝑙}_N\}}(N_M)]$

»Modèle:,, on déduit du principe des actions réciproques en dynamique newtonienne Modèle:Nobr dans chaque résultante partielle

${\overrightarrow{F}}_{\text{int. de champ}}$

et

${\overrightarrow{F}}_{\text{int. de contact}}$

en regroupant les termes par couples

$)$

la nullité de chaque résultante partielle et par suite « la nullité de la résultante des forces intérieures s’exerçant sur un système continu fermé d'expansion surfacique en dynamique newtonienne »

$($

on établit de la même façon que la propriété reste applicable en dynamique relativiste

$)$

soit

«${\overrightarrow{F}}_{\text{int}}=\overrightarrow{0}$».

Modèle:AlModèle:TransparentLa résultante des forces intérieures

${\overrightarrow{F}}_{\text{int}}$

s’exerçant sur le système continu fermé de matière d'expansion linéique

$\left(\mathrm{\Gamma }\right)$

étant définie selon «

${\overrightarrow{F}}_{\text{int}}={\overrightarrow{F}}_{\text{int. de champ}}+{\overrightarrow{F}}_{\text{int. de contact}}$

» avec Modèle:Nobr

$=\int \underset{(M,M^{\prime })\in {\left(\mathrm{\Gamma }\right)}^2}{\int }{d}^2{\overrightarrow{F}}_{\{M,d{𝑙}_M\}\leftarrow \{M^{\prime },d{𝑙}_{M^{\prime }}\}}(M)$

»Modèle:, et «

${\overrightarrow{F}}_{\text{int. de contact}}=$ $\underset{M\in \left(\mathrm{\Gamma }\right)}{\int }[{\overrightarrow{f}}_{M\leftarrow M_g}(M)+{\overrightarrow{f}}_{M\leftarrow M_d}(M)]d{𝑙}_M$

»Modèle:,, on déduit du principe des actions réciproques en dynamique newtonienne Modèle:Nobr dans chaque résultante partielle

${\overrightarrow{F}}_{\text{int. de champ}}$

et

${\overrightarrow{F}}_{\text{int. de contact}}$

en regroupant les termes par couples

$)$

la nullité de chaque résultante partielle et par suite « la nullité de la résultante des forces intérieures s’exerçant sur un système continu fermé d'expansion linéique en dynamique newtonienne »

$($

on établit de la même façon que la propriété reste applicable en dynamique relativiste

$)$

soit

«${\overrightarrow{F}}_{\text{int}}=\overrightarrow{0}$».

Vecteur moment résultant des forces intérieures s’exerçant sur un système discret fermé de points matériels par rapport à un « point origine quelconque A », moment résultant scalaire de ces forces intérieures par rapport à un « axe quelconque Δ »

Vecteur moment résultant des forces intérieures s’exerçant sur un système discret fermé de points matériels par rapport à un point origine A quelconque

Modèle:AlLe vecteur moment résultant, par rapport au point origine

$A$

, des forces intérieures s’exerçant sur le système discret fermé de points matériels

${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$

avec Modèle:Nobr est définie selon

«${\overrightarrow{ℳ}}_{A,\text{int}}=\sum _{i=1..N}\left[\sum _{j=1..N}^{j\ne i}{\overrightarrow{ℳ}}_A\left({\overrightarrow{F}}_{i\leftarrow j}\right)\right]=\sum _{i=1..N}[\sum _{j=1..N}^{j\ne i}\overrightarrow{A{M}_i}\wedge {\overrightarrow{F}}_{i\leftarrow j}]=\sum _{i=1..N}[\sum _{j=1..i-1}^{j=i+1..N}\overrightarrow{A{M}_i}\wedge {\overrightarrow{F}}_{i\leftarrow j}]$» ;

Modèle:Alon déduit du principe des actions réciproques en dynamique newtonienne « la nullité du moment résultant vectoriel des forces intérieures s’exerçant sur un système de points matériels fermé en dynamique newtonienne par rapport à un point origine

$A$

quelconque »

$($

on établit de la même façon que la propriété reste applicable en dynamique relativiste

$)$

soit

«${\overrightarrow{ℳ}}_{A,\text{int}}=\overrightarrow{0}$».

Modèle:AlDémonstration : « en associant les termes de la somme $\sum _{i=1..N}[\sum _{j=1..i-1}^{j=i+1..N}\overrightarrow{A{M}_i}\wedge {\overrightarrow{F}}_{i\leftarrow j}]$ par couple $\{\overrightarrow{A{M}_i}\wedge {\overrightarrow{F}}_{i\leftarrow j},\overrightarrow{A{M}_j}\wedge {\overrightarrow{F}}_{j\leftarrow i}\}$» dont la somme vaut «$\overrightarrow{A{M}_i}\wedge {\overrightarrow{F}}_{i\leftarrow j}+\overrightarrow{A{M}_j}\wedge {\overrightarrow{F}}_{j\leftarrow i}=$ $\overrightarrow{A{M}_i}\wedge {\overrightarrow{F}}_{i\leftarrow j}+\overrightarrow{A{M}_j}\wedge (-{\overrightarrow{F}}_{i\leftarrow j})$ après avoir utilisé la 1^ère relation du principe des actions réciproques à savoir ${\overrightarrow{F}}_{j\leftarrow i}=-{\overrightarrow{F}}_{i\leftarrow j}$» ou encore, après « factorisation vectorielle à droite par ${\overrightarrow{F}}_{i\leftarrow j}$» et utilisation de la relation de Chasles sur l’autre facteur «$[\overrightarrow{A{M}_i}-\overrightarrow{A{M}_j}]\wedge {\overrightarrow{F}}_{i\leftarrow j}=\overrightarrow{M_j{M}_i}\wedge {\overrightarrow{F}}_{i\leftarrow j}=\overrightarrow{0}$ par la 2^ème partie du principe des actions réciproques » d'où la nullité de chaque somme de couple «$\overrightarrow{A{M}_i}\wedge {\overrightarrow{F}}_{i\leftarrow j}+\overrightarrow{A{M}_j}\wedge {\overrightarrow{F}}_{j\leftarrow i}=\overrightarrow{0}$» et par suite, en faisant la somme sur tous les couples différents possibles «${\overrightarrow{ℳ}}_{A,\text{int}}=\overrightarrow{0}$».

Moment résultant scalaire des forces intérieures s’exerçant sur un système discret fermé de points matériels par rapport à un axe Δ quelconque

Modèle:AlDe la propriété du vecteur moment résultant des forces intérieures s’exerçant sur le système discret fermé de points matériels

${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$ $N\in {\mathbb{N}}^{*}\mathrm{\setminus }\left\{1\right\}]$

par rapport à un point origine

$A$

quelconque, soit «

${\overrightarrow{ℳ}}_{A,\text{int}}=\overrightarrow{0},\mathrm{\forall }A\in ℰ$

» et
Modèle:Alde la définition d'un moment scalaire relativement à un axe

$\mathrm{\Delta }$

à partir du vecteur moment relativement à un point

$A$

de l'axe, ce dernier étant orienté par le vecteur unitaire

${\overrightarrow{u}}_{\mathrm{\Delta }}$

, on en tire
Modèle:Alla définition du moment scalaire des forces intérieures s’exerçant sur le système discret fermé de points matériels

${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$ $N\in {\mathbb{N}}^{*}\mathrm{\setminus }\left\{1\right\}]$

par rapport à un axe

$\mathrm{\Delta }$

quelconque, «

${ℳ}_{\mathrm{\Delta },\text{int}}={\overrightarrow{ℳ}}_{A,\text{int}}\cdot {\overrightarrow{u}}_{\mathrm{\Delta }},\mathrm{\forall }A\in \mathrm{\Delta },\mathrm{\forall }\mathrm{\Delta }\subset ℰ$

» puis
Modèle:Alon en déduit « la nullité du moment résultant scalaire des forces intérieures s’exerçant sur un système de points matériels fermé en dynamique newtonienne

$($

et aussi relativiste

$)$

par rapport à un axe

$\mathrm{\Delta }$

quelconque » soit

«${ℳ}_{\mathrm{\Delta },\text{int}}=0,\mathrm{\forall }\mathrm{\Delta }\subset ℰ$».

Généralisation : vecteur moment résultant des forces intérieures s’exerçant sur un système continu fermé de matière par rapport à un « point origine quelconque A », moment scalaire résultant de ces forces intérieures par rapport à un « axe quelconque Δ »

Vecteur moment résultant des forces intérieures s’exerçant sur un système continu fermé de matière par rapport à un point origine A quelconque

Modèle:AlDu vecteur moment résultant par rapport au point origine quelconque

$A$

des forces intérieures

${\overrightarrow{ℳ}}_{A,\text{int}}$

s’exerçant sur le système continu fermé de matière d'expansion tridimensionnelle

$\left(𝒱\right)$

défini selon «

${\overrightarrow{ℳ}}_{A,\text{int}}={\overrightarrow{ℳ}}_{A,\text{int. de champ}}+{\overrightarrow{ℳ}}_{A,\text{int. de contact}}$

» avec «

${\overrightarrow{ℳ}}_{A,\text{int. de champ}}=$ $\iiint \underset{(M,M^{\prime })\in {\left(𝒱\right)}^2}{\iiint }{\overrightarrow{ℳ}}_A[d^2{\overrightarrow{F}}_{\{M,d{𝒱}_M\}\leftarrow \{M^{\prime },d{𝒱}_{M^{\prime }}\}}(M)]=\iiint \underset{(M,M^{\prime })\in {\left(𝒱\right)}^2}{\iiint }\overrightarrow{AM}\wedge d^2{\overrightarrow{F}}_{\{M,d{𝒱}_M\}\leftarrow \{M^{\prime },d{𝒱}_{M^{\prime }}\}}(M)$

»Modèle:, et Modèle:Nobr

$\underset{M\in \left(𝒱\right)}{\iiint }\left\{\underset{N_M\in d{S}_M}{\text{∯}}{\overrightarrow{ℳ}}_A[d^2{\overrightarrow{F}}_{S,\{N_M,d^2{S}_N\}\leftarrow \{N_{\text{voisin de }{N}_M},d^2{S}_N\}}(N_M)]\right\}$

»Modèle:,, on déduit de l'utilisation successive de la 1^ère et 2^ème parties du principe des actions réciproques en dynamique newtonienne Modèle:Nobr dans chaque vecteur moment résultant partiel

${\overrightarrow{ℳ}}_{A,\text{int. de champ}}$

et

${\overrightarrow{ℳ}}_{A,\text{int. de contact}}$

en regroupant les termes par couples

$)$

la nullité de chaque vecteur moment résultant partielModèle:, et par suite « la nullité du vecteur moment résultant des forces intérieures s’exerçant sur un système continu fermé d'expansion tridimensionnelle en dynamique newtonienne par rapport à un point origine

$A$

quelconque »

$($

on établit de la même façon que la propriété reste applicable en dynamique relativiste

$)$

soit

«${\overrightarrow{ℳ}}_{A,\text{int}}=\overrightarrow{0},\mathrm{\forall }A\in ℰ$».

Modèle:AlRemarques : Ce qui vient d'être établi pour un système continu fermé de matière d'expansion tridimensionnelle est encore applicable pour un système continu fermé de matière d'expansion surfacique ou linéique, les seules modifications portant sur le type d'intégrales y intervenant :

Modèle:AlModèle:TransparentLe vecteur moment résultant relativement à un point origine

$A$

quelconque des forces intérieures s’exerçant sur le système continu fermé de matière d'expansion surfacique

$\left(𝒮\right)$

étant défini selon «

${\overrightarrow{ℳ}}_{A,\text{int}}={\overrightarrow{ℳ}}_{A,\text{int. de champ}}+{\overrightarrow{ℳ}}_{A,\text{int. de contact}}$

» avec «

${\overrightarrow{ℳ}}_{A,\text{int. de champ}}=$ $\iint \underset{(M,M^{\prime })\in {\left(𝒮\right)}^2}{\iint }{\overrightarrow{ℳ}}_A[d^2{\overrightarrow{F}}_{\{M,d{𝒮}_M\}\leftarrow \{M^{\prime },d{𝒮}_{M^{\prime }}\}}(M)]=\iint \underset{(M,M^{\prime })\in {\left(𝒮\right)}^2}{\iint }\overrightarrow{AM}\wedge d^2{\overrightarrow{F}}_{\{M,d{𝒮}_M\}\leftarrow \{M^{\prime },d{𝒮}_{M^{\prime }}\}}(M)$

»Modèle:, et «

${\overrightarrow{ℳ}}_{A,\text{int. de contact}}=$ $\underset{M\in \left(𝒮\right)}{\iint }\left\{\underset{N_M\in d{𝑙}_M}{\oint }{\overrightarrow{ℳ}}_A[d^2{\overrightarrow{F}}_{𝑙,\{N_M,d^2{𝑙}_N\}\leftarrow \{N_{\text{voisin de }{N}_M},d^2{𝑙}_N\}}(N_M)]\right\}$

»Modèle:,, on déduit de l'utilisation successive de la 1^ère et 2^ème parties du principe des actions réciproques en dynamique newtonienne Modèle:Nobr dans chaque vecteur moment résultant partiel

${\overrightarrow{ℳ}}_{A,\text{int. de champ}}$

et

${\overrightarrow{ℳ}}_{A,\text{int. de contact}}$

en regroupant les termes par couples

$)$

la nullité de chaque vecteur moment résultant partielModèle:, et par suite « la nullité du vecteur moment résultant des forces intérieures s’exerçant sur un système continu fermé d'expansion surfacique en dynamique newtonienne par rapport à un point origine

$A$

quelconque »

$($

on établit de la même façon que la propriété reste applicable en dynamique relativiste

$)$

soit

«${\overrightarrow{ℳ}}_{A,\text{int}}=\overrightarrow{0},\mathrm{\forall }A\in ℰ$».

Modèle:AlModèle:TransparentLe moment résultant

$($

vectoriel

$)$

relativement à un point origine

$A$

quelconque des forces intérieures s’exerçant sur le système continu fermé de matière d'expansion linéique

$\left(\mathrm{\Gamma }\right)$

étant défini selon «

${\overrightarrow{ℳ}}_{A,\text{int}}={\overrightarrow{ℳ}}_{A,\text{int. de champ}}+{\overrightarrow{ℳ}}_{A,\text{int. de contact}}$

» avec «

${\overrightarrow{ℳ}}_{A,\text{int. de champ}}=$ $\int \underset{(M,M^{\prime })\in {\left(\mathrm{\Gamma }\right)}^2}{\int }{\overrightarrow{ℳ}}_A[d^2{\overrightarrow{F}}_{\{M,d{𝑙}_M\}\leftarrow \{M^{\prime },d{𝑙}_{M^{\prime }}\}}(M)]=\int \underset{(M,M^{\prime })\in {\left(\mathrm{\Gamma }\right)}^2}{\int }\overrightarrow{AM}\wedge d^2{\overrightarrow{F}}_{\{M,d{𝑙}_M\}\leftarrow \{M^{\prime },d{𝑙}_{M^{\prime }}\}}(M)$

»Modèle:, et «

${\overrightarrow{ℳ}}_{A,\text{int. de contact}}=$ $\underset{M\in \left(\mathrm{\Gamma }\right)}{\int }\overrightarrow{AM}\wedge [{\overrightarrow{f}}_{M\leftarrow M_g}(M)+{\overrightarrow{f}}_{M\leftarrow M_d}(M)]d{𝑙}_M$

»Modèle:,, on déduit de l'utilisation successive de la 1^ère et 2^ème parties du principe des actions réciproques en dynamique Modèle:Nobr Modèle:Nobr dans chaque vecteur moment résultant partiel

${\overrightarrow{ℳ}}_{A,\text{int. de champ}}$

et

${\overrightarrow{ℳ}}_{A,\text{int. de contact}}$

en regroupant les termes par couples

$)$

la nullité de chaque vecteur moment résultant Modèle:Nobr et par suite « la nullité du vecteur moment résultant des forces intérieures s’exerçant sur un système continu fermé d'expansion linéique en dynamique newtonienne par rapport à un point origine

$A$ $($

on établit de la même façon que la propriété reste applicable en dynamique relativiste

$)$

soit

«${\overrightarrow{ℳ}}_{A,\text{int}}=\overrightarrow{0},\mathrm{\forall }A\in ℰ$».

Moment résultant scalaire des forces intérieures s’exerçant sur un système continu fermé de matière par rapport à un axe Δ quelconque

Modèle:AlDe la propriété du vecteur moment résultant des forces intérieures s’exerçant sur un système fermé discret de points matériels ou continu de matière d'expansion volumique, surfacique ou linéique par rapport à un point origine

$A$

quelconque, soit «

${\overrightarrow{ℳ}}_{A,\text{int}}=\overrightarrow{0},\mathrm{\forall }A\in ℰ$

» et
Modèle:Alde la définition d'un moment scalaire relativement à un axe

$\mathrm{\Delta }$

à partir du vecteur moment relativement à un point

$A$

de l'axe, ce dernier étant orienté par le vecteur unitaire

${\overrightarrow{u}}_{\mathrm{\Delta }}$

, on en tire
Modèle:Alla définition du moment scalaire des forces intérieures s’exerçant sur un système fermé discret de points matériels ou continu de matière d'expansion volumique, surfacique ou linéique par rapport à un axe

$\mathrm{\Delta }$

quelconque, «

${ℳ}_{\mathrm{\Delta },\text{int}}={\overrightarrow{ℳ}}_{A,\text{int}}\cdot {\overrightarrow{u}}_{\mathrm{\Delta }},\mathrm{\forall }A\in \mathrm{\Delta },\mathrm{\forall }\mathrm{\Delta }\subset ℰ$

» puis
Modèle:Alon en déduit « la nullité du moment résultant scalaire des forces intérieures s’exerçant sur un système fermé discret de points matériels ou continu de matière d'expansion volumique, surfacique ou linéique en dynamique newtonienne

$($

et aussi relativiste

$)$

par rapport à un axe

$\mathrm{\Delta }$

quelconque » soit

«${ℳ}_{\mathrm{\Delta },\text{int}}=0,\mathrm{\forall }\mathrm{\Delta }\subset ℰ$».

Commentaire sur la nullité de la résultante et du vecteur moment résultant des forces intérieures s’exerçant sur un système fermé de matière

Modèle:AlBien que le système des forces intérieures s'exerçant sur un système fermé de matière ait une résultante nulle et un moment résultant par rapport à un point origine quelconque également nul, il n’est pas, a priori, équivalent à un système de forces nulles $\{$nous verrons dans le paragraphe « conséquences diverses de la définition de la puissance des forces intérieures appliquées à un système de matière relativement à un référentiel d'étude » du chap.$10$ de la leçon « Mécanique 2 (PCSI) », que la puissance développée par les forces intérieures n’est pas nulle si le système de matière est déformable alors qu'un système de forces nulles ne développe évidemment aucune puissance$\dots \}$.

Modèle:AlRemarque : en utilisant la notion $($hors programme de physique de P.C.S.I.$)$ de « torseur » introduite dans le chap.$1$ de la leçon « Outils mathématiques pour la physique - bis (PCSI) », l'ensemble de la résultante et du moment résultant par rapport à un point origine quelconque $A$ des forces intérieures s'exerçant sur un système fermé de matière constitue les éléments de réduction en $A$ du torseur Modèle:Nobr des forces intérieures s'exerçant sur le système fermé de matière soit «${𝒯}_{\text{stat. int}}={\left\{\begin{array}{c}{\overrightarrow{F}}_{\text{int}}=\overrightarrow{0}\\ {\overrightarrow{ℳ}}_{A,\text{int}}=\overrightarrow{0}\end{array}\right\}}_A,\mathrm{\forall }A\in ℰ$», le torseur statique des forces intérieures s'exerçant sur le système fermé de matière est donc le torseur nul $[$d'après la définition donnée dans le chap.$1$ de la leçon « Outils mathématiques pour la physique - bis (PCSI) »$]$ ;
Modèle:AlModèle:Transparenttoutefois si le torseur statique des forces intérieures s'exerçant sur le système fermé de matière est le torseur nul, ce n'est pas le torseur de forces nulles.

Résultante dynamique, moments résultants dynamiques vectoriel et scalaire appliqués à un système de points matériels

Modèle:AlLes notions de résultante dynamique et de moments résultants dynamiques vectoriel et scalaire sont introduites dans le cadre de la dynamique newtonienne mais elle reste applicable en dynamique relativiste.

Rappel : résultante dynamique appliquée à un système discret fermé de points matériels

Modèle:AlLa résultante dynamique appliquée au système discret fermé de points matériels

${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$

avec Modèle:Nobr est la résultante des forces extérieures

${\overrightarrow{F}}_{\text{ext}}$

s’exerçant sur ce système Modèle:Nobr 1^ère introduction dans le paragraphe « définition de la résultante dynamique s'exerçant sur un système (discret) de points matériels fermé » du chap.

$6$

de la leçon « Mécanique 1 (PCSI) »

$]$

c'est-à-dire

«${\overrightarrow{F}}_{\text{ext}}=\sum _{i=1}^{i=N}{\overrightarrow{F}}_{i\leftarrow \text{ext}}$» avec
«${\overrightarrow{F}}_{i\leftarrow \text{ext}}=\sum _k{\overrightarrow{F}}_{i\leftarrow \left\{{\text{ext}}_k\right\}}$ la somme des forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:Transparent exerce sur chaque point matériel $M_i$ du système ».

Complément : résultante dynamique appliquée à un système continu fermé de matière

Modèle:AlLa définition de la résultante dynamique appliquée à un système continu fermé de matière d'expansion tridimensionnelle, surfacique ou linéique est calquée sur celle d'un système discret fermé de points matériels, les seules modifications consistant à remplacer les sommes discrètes par des sommes continues $($c'est-à-dire mettant en œuvre une intégrale volumique, surfacique ou curviligne$)$ d'où :

$\succ$

La résultante dynamique appliquée au système continu fermé de matière d'expansion volumique

$\left(𝒱\right)$

est la résultante des forces extérieures

${\overrightarrow{F}}_{\text{ext}}$

s’exerçant sur ce système c'est-à-dire

«${\overrightarrow{F}}_{\text{ext}}=\underset{M\in \left(𝒱\right)}{\iiint }d{\overrightarrow{F}}_{V,\{M,d{𝒱}_M\}\leftarrow \text{ext}}(M)=\underset{M\in \left(𝒱\right)}{\iiint }{\overrightarrow{f}}_{V,M\leftarrow \text{ext}}(M)d{𝒱}_M$» avec
«$d{\overrightarrow{F}}_{V,\{M,d{𝒱}_M\}\leftarrow \text{ext}}(M)=\sum _{k}d{\overrightarrow{F}}_{V,\{M,d{𝒱}_M\}\leftarrow {\text{ext}}_k}(M)$ la somme des forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:AlModèle:Transparent exerce sur chaque pseudo point $(M,d{𝒱}_M)$ du système »
ou «${\overrightarrow{f}}_{V,M\leftarrow \text{ext}}(M)=\sum _k{\overrightarrow{f}}_{V,M\leftarrow {\text{ext}}_k}(M)$ la somme des densités volumiques de forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:AlModèle:Transparent exerce en chaque point $M$ de l'expansion volumique du système ». $\succ$

La résultante dynamique appliquée au système continu fermé de matière d'expansion surfacique

$\left(𝒮\right)$

est la résultante des forces extérieures

${\overrightarrow{F}}_{\text{ext}}$

s’exerçant sur ce système c'est-à-dire

«${\overrightarrow{F}}_{\text{ext}}=\underset{M\in \left(𝒮\right)}{\iint }d{\overrightarrow{F}}_{S,\{M,d{S}_M\}\leftarrow \text{ext}}(M)=\underset{M\in \left(𝒮\right)}{\iint }{\overrightarrow{f}}_{S,M\leftarrow \text{ext}}(M)d{S}_M$» avec
«$d{\overrightarrow{F}}_{S,\{M,d{S}_M\}\leftarrow \text{ext}}(M)=\sum _{k}d{\overrightarrow{F}}_{S,\{M,d{S}_M\}\leftarrow {\text{ext}}_k}(M)$ la somme des forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:Transparent exerce sur chaque pseudo point $(M,d{S}_M)$ du système »
ou «${\overrightarrow{f}}_{S,M\leftarrow \text{ext}}(M)=\sum _k{\overrightarrow{f}}_{S,M\leftarrow {\text{ext}}_k}(M)$ la somme des densités surfaciques de forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:AlModèle:Transparent exerce en chaque point $M$ de l'expansion surfacique du système ». $\succ$

La résultante dynamique appliquée au système continu fermé de matière d'expansion linéique

$\left(\mathrm{\Gamma }\right)$

est la résultante des forces extérieures

${\overrightarrow{F}}_{\text{ext}}$

s’exerçant sur ce système c'est-à-dire

«${\overrightarrow{F}}_{\text{ext}}=\underset{M\in \left(\mathrm{\Gamma }\right)}{\int }d{\overrightarrow{F}}_{𝑙,\{M,d{𝑙}_M\}\leftarrow \text{ext}}(M)=\underset{M\in \left(\mathrm{\Gamma }\right)}{\int }{\overrightarrow{f}}_{𝑙,M\leftarrow \text{ext}}(M)d{𝑙}_M$» avec
«$d{\overrightarrow{F}}_{𝑙,\{M,d{𝑙}_M\}\leftarrow \text{ext}}(M)=\sum _{k}d{\overrightarrow{F}}_{𝑙,\{M,d{𝑙}_M\}\leftarrow {\text{ext}}_k}(M)$ la somme des forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:AlModèle:Transparent exerce sur chaque pseudo point $(M,d{𝑙}_M)$ du système »
ou «${\overrightarrow{f}}_{𝑙,M\leftarrow \text{ext}}(M)=\sum _k{\overrightarrow{f}}_{𝑙,M\leftarrow {\text{ext}}_k}(M)$ la somme des densités linéiques de forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:AlModèle:Transparent exerce en chaque point $M$ de l'expansion linéique du système ».

Complément : Vecteur moment résultant dynamique appliqué à un système continu fermé de matière relativement à un point origine « quelconque A »

Modèle:AlLa définition du vecteur moment résultant dynamique appliqué à un système continu fermé de matière d'expansion tridimensionnelle, surfacique ou linéique évalué relativement à un point origine $A$ quelconque est calquée sur celle d'un système discret fermé de points matériels, les seules modifications consistant à remplacer les sommes discrètes par des sommes continues $($c'est-à-dire mettant en œuvre une intégrale volumique, Modèle:Nobr ou curviligne$)$ d'où :

$\succ$

Le vecteur moment résultant dynamique appliqué au système continu fermé de matière d'expansion volumique

$\left(𝒱\right)$

évalué relativement à un point origine

$A$

quelconque est le vecteur moment résultant des forces extérieures s’exerçant sur ce système évalué par rapport à

$A$

c'est-à-dire

«${\overrightarrow{ℳ}}_{A,\text{ext}}=\underset{M\in \left(𝒱\right)}{\iiint }{\overrightarrow{ℳ}}_A[d{\overrightarrow{F}}_{V,\{M,d{𝒱}_M\}\leftarrow \text{ext}}(M)]=\underset{M\in \left(𝒱\right)}{\iiint }\overrightarrow{AM}\wedge {\overrightarrow{f}}_{V,M\leftarrow \text{ext}}(M)d{𝒱}_M$» avec
«$d{\overrightarrow{F}}_{V,\{M,d{𝒱}_M\}\leftarrow \text{ext}}(M)=\sum _{k}d{\overrightarrow{F}}_{V,\{M,d{𝒱}_M\}\leftarrow {\text{ext}}_k}(M)$ la somme des forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:AlModèle:Transparent exerce sur chaque pseudo point $(M,d{𝒱}_M)$ du système »
ou «${\overrightarrow{f}}_{V,M\leftarrow \text{ext}}(M)=\sum _k{\overrightarrow{f}}_{V,M\leftarrow {\text{ext}}_k}(M)$ la somme des densités volumiques de forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:AlModèle:Transparent exerce en chaque point $M$ de l'expansion volumique du système ». $\succ$

Le vecteur moment résultant dynamique appliqué au système continu fermé de matière d'expansion surfacique

$\left(𝒮\right)$

évalué relativement à un point origine

$A$

quelconque est le vecteur moment résultant des forces extérieures s’exerçant sur ce système évalué par rapport à

$A$

c'est-à-dire

«${\overrightarrow{ℳ}}_{A,\text{ext}}=\underset{M\in \left(𝒮\right)}{\iint }{\overrightarrow{ℳ}}_A[d{\overrightarrow{F}}_{S,\{M,d{S}_M\}\leftarrow \text{ext}}(M)]=\underset{M\in \left(𝒮\right)}{\iint }\overrightarrow{AM}\wedge {\overrightarrow{f}}_{S,M\leftarrow \text{ext}}(M)d{S}_M$» avec
«$d{\overrightarrow{F}}_{S,\{M,d{S}_M\}\leftarrow \text{ext}}(M)=\sum _{k}d{\overrightarrow{F}}_{S,\{M,d{S}_M\}\leftarrow {\text{ext}}_k}(M)$ la somme des forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:AlModèle:Transparent exerce sur chaque pseudo point $(M,d{S}_M)$ du système »
ou «${\overrightarrow{f}}_{S,M\leftarrow \text{ext}}(M)=\sum _k{\overrightarrow{f}}_{S,M\leftarrow {\text{ext}}_k}(M)$ la somme des densités surfaciques de forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:AlModèle:Transparent exerce en chaque point $M$ de l'expansion surfacique du système ». $\succ$

Le vecteur moment résultant dynamique appliqué au système continu fermé de matière d'expansion linéique

$\left(\mathrm{\Gamma }\right)$

évalué relativement à un point origine

$A$

quelconque est le vecteur moment résultant des forces extérieures s’exerçant sur ce système évalué par rapport à

$A$

c'est-à-dire

«${\overrightarrow{ℳ}}_{A,\text{ext}}=\underset{M\in \left(\mathrm{\Gamma }\right)}{\int }{\overrightarrow{ℳ}}_A[d{\overrightarrow{F}}_{𝑙,\{M,d{𝑙}_M\}\leftarrow \text{ext}}(M)]=\underset{M\in \left(\mathrm{\Gamma }\right)}{\int }\overrightarrow{AM}\wedge {\overrightarrow{f}}_{𝑙,M\leftarrow \text{ext}}(M)d{𝑙}_M$» avec
«$d{\overrightarrow{F}}_{𝑙,\{M,d{𝑙}_M\}\leftarrow \text{ext}}(M)=\sum _{k}d{\overrightarrow{F}}_{𝑙,\{M,d{𝑙}_M\}\leftarrow {\text{ext}}_k}(M)$ la somme des forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:AlModèle:Transparent exerce sur chaque pseudo point $(M,d{𝑙}_M)$ du système »
ou «${\overrightarrow{f}}_{𝑙,M\leftarrow \text{ext}}(M)=\sum _k{\overrightarrow{f}}_{𝑙,M\leftarrow {\text{ext}}_k}(M)$ la somme des densités linéiques de forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur
Modèle:AlModèle:Transparent exerce en chaque point $M$ de l'expansion linéique du système ».

Complément : vecteurs résultante et moment résultant dynamiques s'exerçant sur un système discret (ou continu) fermé de matière, éléments de réduction du torseur dynamique de ce système

Modèle:AlSelon la notion $($hors programme de physique de P.C.S.I.$)$ de « torseur » introduite dans le chap.$1$ de la leçon « Outils mathématiques pour la physique - bis (PCSI) », l'ensemble des vecteurs résultante et moment résultant par rapport à un point origine quelconque $A$ dynamiques s'exerçant sur un système fermé de matière constitue les éléments de réduction en $A$ du torseur statiqueModèle:, des forces extérieures ${𝒯}_{\text{stat. ext}}$ s'exerçant sur ce système fermé de matière, d'où «${𝒯}_{\text{stat. ext}}={\left\{\begin{array}{c}{\overrightarrow{F}}_{\text{ext}}\\ {\overrightarrow{ℳ}}_{A,\text{ext}}=\end{array}\right\}}_A,\mathrm{\forall }A\in ℰ$».

Moment résultant scalaire dynamique appliqué à un système discret fermé de points matériels relativement à un axe « quelconque Δ »

Modèle:AlDe la définition du vecteur moment résultant dynamique s’exerçant sur le système discret fermé de points matériels ${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$ $[$avec $N\in {\mathbb{N}}^{*}\mathrm{\setminus }\left\{1\right\}]$ par rapport à un point origine $A$ quelconque, soit «${\overrightarrow{ℳ}}_{A,\text{ext}}=\sum _{i=1}^{i=N}{\overrightarrow{ℳ}}_A\left[{\overrightarrow{F}}_{i\leftarrow \text{ext}}\right]=\sum _{i=1}^{i=N}\overrightarrow{A{M}_i}\wedge {\overrightarrow{F}}_{i\leftarrow \text{ext}},\mathrm{\forall }A\in ℰ$» avec «${\overrightarrow{F}}_{i\leftarrow \text{ext}}=\sum _k{\overrightarrow{F}}_{i\leftarrow \left\{{\text{ext}}_k\right\}}$ la somme des forces que chaque système $({\mathrm{\Sigma }}_k)$ extérieur exerce sur $M_i$» ainsi que
Modèle:Alde la définition d'un moment scalaire relativement à un axe $\mathrm{\Delta }$ à partir du vecteur moment relativement à un point $A$ de l'axe, ce dernier étant orienté par le vecteur unitaire ${\overrightarrow{u}}_{\mathrm{\Delta }}$, on en tire
Modèle:AlModèle:Transparentla définition du moment résultant dynamique scalaire s’exerçant sur le système discret fermé de points matériels ${\left\{M_i\left(m_i\right)\right\}}_{i\in \left[[1,N]\right]}$ Modèle:Nobr $N\in {\mathbb{N}}^{*}\mathrm{\setminus }\left\{1\right\}]$ par rapport à un axe $\mathrm{\Delta }$ quelconque, Modèle:Nobr ${\overrightarrow{ℳ}}_{A,\text{ext}}\cdot {\overrightarrow{u}}_{\mathrm{\Delta }},\mathrm{\forall }A\in \mathrm{\Delta },\mathrm{\forall }\mathrm{\Delta }\subset ℰ$», soit encore «${ℳ}_{\mathrm{\Delta },\text{ext}}=[\sum _{i=1}^{i=N}\overrightarrow{A{M}_i}\wedge {\overrightarrow{F}}_{i\leftarrow \text{ext}}]\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}=\sum _{i=1}^{i=N}[(\overrightarrow{A{M}_i}\wedge {\overrightarrow{F}}_{i\leftarrow \text{ext}})\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}]=\sum _{i=1}^{i=N}{ℳ}_{\mathrm{\Delta }}\left[{\overrightarrow{F}}_{i\leftarrow \text{ext}}\right]$». Modèle:Définition

Complément : moment résultant scalaire dynamique appliqué à un système continu fermé de matière relativement à un axe « quelconque Δ »

Modèle:AlLa définition du vecteur moment résultant dynamique appliqué à un système continu fermé de matière d'expansion tridimensionnelle, surfacique ou linéique évalué relativement à un point origine $A$ quelconque étant calquée sur celle d'un système discret fermé de points matériels, avec pour seules modifications le remplacement des sommes discrètes par des sommes continues $($c'est-à-dire mettant en œuvre une intégrale volumique, Modèle:Nobr ou curviligne$)$ et
Modèle:Alcelle du moment résultant dynamique scalaire d'un système discret fermé de points matériels relativement à un axe $\mathrm{\Delta }$ s'obtenant par multiplication scalaire du vecteur moment résultant dynamique appliqué à ce système en n'importe quel point $A\in \mathrm{\Delta }$ par le vecteur unitaire ${\overrightarrow{u}}_{\mathrm{\Delta }}$ orientant $\mathrm{\Delta }$ avec utilisation de la distributivité de la multiplication scalaire relativement à l'addition vectorielle,
Modèle:Alon en déduit la définition du moment résultant dynamique scalaire d'un système continu fermé de matière d'expansion tridimensionnelle, surfacique ou linéique relativement à un axe $\mathrm{\Delta }$ utilisant

• d'une part la définition générale d'un moment scalaire relativement à un moment vectoriel et
• d'autre part la propriété de « distributivité de la multiplication scalaire relativement à l'intégration vectorielle » :

Changement d’origine de calcul du moment résultant dynamique vectoriel appliqué à un système de points matériels

Changement d’origine de calcul du vecteur moment résultant dynamique appliqué à un système discret fermé de points matériels

Modèle:AlÀ partir du changement d'origine du « vecteur moment d'une force

$\overrightarrow{F}(M)$

appliquée à un point matériel

$M$

par rapport à un point origine

$A$

à l'instant

$t$

» défini dans le paragraphe « changement d'origine de calcul du moment vectoriel d'une force » plus haut dans ce chapitre, à savoir,

«$\mathrm{\forall }(O,O^{\prime })\in {ℰ}^2,{\overrightarrow{ℳ}}_{O^{\prime }}[\overrightarrow{F}(M),t]={\overrightarrow{ℳ}}_O[\overrightarrow{F}(M),t]+\overrightarrow{O^{\prime }O}\wedge \overrightarrow{F}(M),\left(𝔠𝔥\right)$» et

Modèle:AlModèle:Transparentde la définition du vecteur moment résultant dynamique appliqué au système discret fermé de points matériels

${\{M_i,\left(m_i\right)\}}_{i=1..N}$ $[$

avec

$N\in {\mathbb{N}}^{*}\mathrm{\setminus }\left\{1\right\}]$

relativement à un point origine

$A$

quelconque, à savoir,

«${\overrightarrow{ℳ}}_{A,\text{ext}}(t)=\sum _{i=1}^{i=N}{\overrightarrow{ℳ}}_A[{\overrightarrow{F}}_{i\leftarrow \text{ext}},t]=\sum _{i=1}^{i=N}\overrightarrow{A{M}_i}(t)\wedge {\overrightarrow{F}}_{i\leftarrow \text{ext}}$» avec
«${\overrightarrow{F}}_{i\leftarrow \text{ext}}=\sum _k{\overrightarrow{F}}_{i\leftarrow \left\{{\text{ext}}_k\right\}}$ somme des forces que les systèmes $({\mathrm{\Sigma }}_k)$ extérieurs exerce sur chaque point $M_i$»,

Modèle:Alon en déduit, par addition vectorielle des relations

$\left(𝔠𝔥\right)$ $\{$

dans lesquelles

$M$

est remplacée par

$M_i,i\in \left[[1,N]\right]$

ainsi que

$(O,O^{\prime })$

par

$(A,A^{\prime })\}$ «$\mathrm{\forall }(A,A^{\prime })\in {ℰ}^2,\sum _{i=1}^{i=N}{\overrightarrow{ℳ}}_{A^{\prime }}[{\overrightarrow{F}}_{i\leftarrow \text{ext}},t]=\sum _{i=1}^{i=N}{\overrightarrow{ℳ}}_A[{\overrightarrow{F}}_{i\leftarrow \text{ext}},t]+[\sum _{i=1}^{i=N}\overrightarrow{A^{\prime }A}\wedge {\overrightarrow{F}}_{i\leftarrow \text{ext}}]$» et

Modèle:AlModèle:Transparent« factorisation vectorielle à gauche par Modèle:Nobr dans le 2^ème terme du 2^ème membre

«$\mathrm{\forall }(A,A^{\prime })\in {ℰ}^2,\sum _{i=1}^{i=N}{\overrightarrow{ℳ}}_{A^{\prime }}[{\overrightarrow{F}}_{i\leftarrow \text{ext}},t]=\sum _{i=1}^{i=N}{\overrightarrow{ℳ}}_A[{\overrightarrow{F}}_{i\leftarrow \text{ext}},t]+\overrightarrow{A^{\prime }A}\wedge \left[\sum _{i=1}^{i=N}{\overrightarrow{F}}_{i\leftarrow \text{ext}}\right]$»
soit finalement «$\mathrm{\forall }(A,A^{\prime })\in {ℰ}^2,{\overrightarrow{ℳ}}_{A^{\prime },\text{ext}}(t)={\overrightarrow{ℳ}}_{A,\text{ext}}(t)+\overrightarrow{A^{\prime }A}\wedge {\overrightarrow{F}}_{\text{ext}}(t)$» avec
«${\overrightarrow{F}}_{\text{ext}}(t)=\sum _k{\overrightarrow{F}}_{{\text{ext}}_k}(t)$ la somme des résultantes dynamiques exercées par tous les systèmes $({\mathrm{\Sigma }}_k)$ extérieurs ».

Complément : changement d’origine de calcul du vecteur moment résultant dynamique appliqué à un système continu fermé de matière

Modèle:AlLes définitions des vecteurs résultante et moment résultant dynamiques appliqués à un système continu fermé de matière d'expansion tridimensionnelle, surfacique ou linéique, moment évalué relativement à un point origine $A$ quelconque, étant calquées sur celle d'un système discret fermé de points matériels, avec pour seules modifications le remplacement des sommes discrètes par des sommes continues Modèle:Nobr mettant en œuvre une intégrale volumique, Modèle:Nobr ou curviligne$)$ et
Modèle:Alla « factorisation vectorielle à gauche dans une intégration vectorielle »Modèle:, se substituant sans restriction à la « factorisation vectorielle à gauche dans une somme discrète vectorielle »,

Modèle:Alon en déduit la formule de changement d'origine de calcul du vecteur moment résultant dynamique appliqué à un système continu fermé de matière d'expansions tridimensionnelle

$\left(𝒱\right)$

, surfacique

$\left(𝒮\right)$

ou linéique

$\left(\mathrm{\Gamma }\right)$

 :

«$\mathrm{\forall }(A,A^{\prime })\in {ℰ}^2,{\overrightarrow{ℳ}}_{A^{\prime },\text{ext}}(t)={\overrightarrow{ℳ}}_{A,\text{ext}}(t)+\overrightarrow{A^{\prime }A}\wedge {\overrightarrow{F}}_{\text{ext}}(t)$» avec
«${\overrightarrow{F}}_{\text{ext}}(t)$ la résultante dynamique exercée sur le système continu fermé
Modèle:Ald'expansions tridimensionnelle $\left(𝒱\right)$, surfacique $\left(𝒮\right)$ ou linéique $\left(\mathrm{\Gamma }\right)$».

Complément : changement d’axe de calcul du moment résultant scalaire dynamique appliqué à un système matériel quand les deux axes gardent une même direction

Modèle:AlSoit

$(\mathrm{\Delta },{\mathrm{\Delta }}^{\prime })$

un couple d'axes

$\parallel$

quelconques tous deux orientés par

${\overrightarrow{u}}_{\mathrm{\Delta }}$

,

$A$

et

$A^{\prime }$

deux points quelconques choisis respectivement sur

$\mathrm{\Delta }$

et

${\mathrm{\Delta }}^{\prime }$

, le changement d'origine du vecteur moment résultant dynamique appliqué au système matériel fermé, qu'il soit discret ou continu d'expansions tridimensionnelle, surfacique ou linéique, s'écrivant

«$\mathrm{\forall }A\in \mathrm{\Delta },\mathrm{\forall }{A}^{\prime }\in {\mathrm{\Delta }}^{\prime },{\overrightarrow{ℳ}}_{A^{\prime },\text{ext}}(t)={\overrightarrow{ℳ}}_{A,\text{ext}}(t)+\overrightarrow{A^{\prime }A}\wedge {\overrightarrow{F}}_{\text{ext}}(t)$» avec
«${\overrightarrow{F}}_{\text{ext}}(t)$ la résultante dynamique exercée sur le système matériel fermé qu'il soit discret ou
Modèle:Alcontinu d'expansions tridimensionnelle $\left(𝒱\right)$, surfacique $\left(𝒮\right)$ ou linéique $\left(\mathrm{\Gamma }\right)$»,

Modèle:Alil suffit, pour obtenir le changement d'axe de calcul du moment résultant scalaire dynamique appliqué au système étudié de multiplier scalairement chaque membre par

${\overrightarrow{u}}_{\mathrm{\Delta }}$

ce qui donne Modèle:Nobr

${\overrightarrow{ℳ}}_{A,\text{ext}}(t)\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}+[\overrightarrow{A^{\prime }A}\wedge {\overrightarrow{F}}_{\text{ext}}(t)]\cdot {\overrightarrow{u}}_{\mathrm{\Delta }}$

» en utilisant la distributivité de la multiplication scalaire relativement à l'addition vectorielle soit finalement

«${ℳ}_{{\mathrm{\Delta }}^{\prime },\text{ext}}(t)={ℳ}_{\mathrm{\Delta },\text{ext}}(t)+[{\overrightarrow{u}}_{\mathrm{\Delta }}\wedge \overrightarrow{A^{\prime }A}]\cdot {\overrightarrow{F}}_{\text{ext}}(t)$» avec
«${\mathrm{\Delta }}^{\prime }\parallel$ à $\mathrm{\Delta }$ de direction ${\overrightarrow{u}}_{\mathrm{\Delta }}$, $\mathrm{\forall }{A}^{\prime }\in {\mathrm{\Delta }}^{\prime },\mathrm{\forall }A\in \mathrm{\Delta }$» ;

Modèle:Alcette formule de changement d'axe devant être indépendante de

$A\in \mathrm{\Delta }$

et de

$A^{\prime }\in {\mathrm{\Delta }}^{\prime }$

, on choisit ces derniers en

$H\in \mathrm{\Delta }$

et

$H^{\prime }\in {\mathrm{\Delta }}^{\prime }$

tels que «

$\overrightarrow{H^{\prime }H}$

soit

$\perp$

à

${\overrightarrow{u}}_{\mathrm{\Delta }}$

»

$[$

ainsi la longueur

$H^{\prime }H$

est la plus courte distance entre les deux axes

$]$

d'où la réécriture de la formule de changement d'axe selon

«${ℳ}_{{\mathrm{\Delta }}^{\prime },\text{ext}}(t)={ℳ}_{\mathrm{\Delta },\text{ext}}(t)+[{\overrightarrow{u}}_{\mathrm{\Delta }}\wedge \overrightarrow{H^{\prime }H}]\cdot {\overrightarrow{F}}_{\text{ext}}(t)$» avec
«${\mathrm{\Delta }}^{\prime }\parallel$ à $\mathrm{\Delta }$ de direction ${\overrightarrow{u}}_{\mathrm{\Delta }}$ et $H^{\prime }\in {\mathrm{\Delta }}^{\prime },H\in \mathrm{\Delta }$ tels que $\overrightarrow{H^{\prime }H}\perp {\overrightarrow{u}}_{\mathrm{\Delta }}$» ;

Modèle:Alle vecteur «${\overrightarrow{u}}_{\mathrm{\Delta }}\wedge \overrightarrow{H^{\prime }H}$» étant $\perp$ au plan $\{\mathrm{\Delta },{\mathrm{\Delta }}^{\prime }\}$ formé par les deux axes, nous en déduisons la discussion suivante selon la disposition de la résultante dynamique ${\overrightarrow{F}}_{\text{ext}}(t)$ du système à l'instant $t$ :

• si la résultante dynamique ${\overrightarrow{F}}_{\text{ext}}(t)$ du système à l'instant $t$ est $\parallel$ au plan $\{\mathrm{\Delta },{\mathrm{\Delta }}^{\prime }\}$ formé par les deux axes, on a $[{\overrightarrow{u}}_{\mathrm{\Delta }}\wedge \overrightarrow{H^{\prime }H}]\cdot {\overrightarrow{F}}_{\text{ext}}(t)=0$ et par suite la formule de changement d'axe se réécrit «${ℳ}_{{\mathrm{\Delta }}^{\prime },\text{ext}}(t)={ℳ}_{\mathrm{\Delta },\text{ext}}(t)$», ${\mathrm{\Delta }}^{\prime }$ étant $\parallel$ à $\mathrm{\Delta }$
  avec «${\overrightarrow{F}}_{\text{ext}}(t)\parallel$ au plan $\{\mathrm{\Delta },{\mathrm{\Delta }}^{\prime }\}$»,
• si la résultante dynamique ${\overrightarrow{F}}_{\text{ext}}(t)$ du système à l'instant $t$ est $\parallel ̸$ au plan $\{\mathrm{\Delta },{\mathrm{\Delta }}^{\prime }\}$ formé par les deux axes et en notant «${\overrightarrow{F}}_{\text{ext},\perp }(t)$ la composante de ${\overrightarrow{F}}_{\text{ext}}(t)\perp$ au plan $\{\mathrm{\Delta },{\mathrm{\Delta }}^{\prime }\}$» ainsi que Modèle:Nobr la distance $($non algébrisée$)$ séparant les deux axes », on en déduit «$[{\overrightarrow{u}}_{\mathrm{\Delta }}\wedge \overrightarrow{H^{\prime }H}]\cdot {\overrightarrow{F}}_{\text{ext}}(t)=\pm \Vert {\overrightarrow{F}}_{\text{ext},\perp }(t)\Vert 𝑑$» $[$avec le signe «$+$» si «${\overrightarrow{F}}_{\text{ext},\perp }(t)$ est de même sens que ${\overrightarrow{u}}_{\mathrm{\Delta }}\wedge \overrightarrow{H^{\prime }H}$» et «$-$» si «${\overrightarrow{F}}_{\text{ext},\perp }(t)$ est de sens contraire à ${\overrightarrow{u}}_{\mathrm{\Delta }}\wedge \overrightarrow{H^{\prime }H}$»$]$ et par suite la formule de changement d'axe se réécrit «${ℳ}_{{\mathrm{\Delta }}^{\prime },\text{ext}}(t)={ℳ}_{\mathrm{\Delta },\text{ext}}(t)\pm \Vert {\overrightarrow{F}}_{\text{ext},\perp }(t)\Vert 𝑑$» où ${\mathrm{\Delta }}^{\prime }$ est $\parallel$ à $\mathrm{\Delta }$
  $[$signe «$+$» si «${\overrightarrow{F}}_{\text{ext},\perp }(t)$ est de même sens que ${\overrightarrow{u}}_{\mathrm{\Delta }}\wedge \overrightarrow{H^{\prime }H}$» et
  $[$signe «$-$» si «${\overrightarrow{F}}_{\text{ext},\perp }(t)$ est de sens contraire à ${\overrightarrow{u}}_{\mathrm{\Delta }}\wedge \overrightarrow{H^{\prime }H}$»$]$Modèle:Al
  avec «${\overrightarrow{F}}_{\text{ext},\perp }(t)$ la composante de ${\overrightarrow{F}}_{\text{ext}}(t)\perp$ au plan $\{\mathrm{\Delta },{\mathrm{\Delta }}^{\prime }\}$» et
  «$𝑑$ la plus courte distance séparant les deux axes ».

Définition d’un couple, propriété du moment vectoriel d’un couple

Définition d'un couple en tant que système de forces

Modèle:Définition Modèle:AlRemarque : Un couple $($en tant que système de forces$)$ est un cas particulier de « torseur » introduit en complément dans le chap.$1$ de la leçon « Outils mathématiques pour la physique - bis (PCSI) », le « torseur couple » défini dans le même chapitre de la même leçon $\dots$

Schémas représentant deux exemples de couples en tant que systèmes de forces

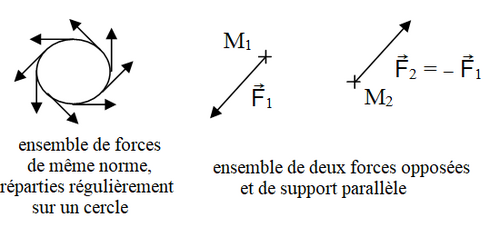
Exemples de couple

Modèle:AlVoir ci-contre :

• exemple de gauche : système de forces de même norme également réparties sur un cercle du système de matière sur lequel le couple s'exerce,
• exemple de droite : deux forces opposées $\{{\overrightarrow{F}}_1,{\overrightarrow{F}}_2=-{\overrightarrow{F}}_1\}$ appliquées respectivement en deux points $(M_1,M_2)$ du système de matière sur lequel le couple s'exerce telles que la direction commune de $\{{\overrightarrow{F}}_1,{\overrightarrow{F}}_2=-{\overrightarrow{F}}_1\}$ soit différente de la direction de $\overrightarrow{M_1{M}_2}$.

Propriété du moment vectoriel d'un couple

Modèle:AlLa résultante d’un couple étant nulle et

Modèle:Alle changement d'origine de calcul du moment résultant vectoriel d'un système de forces de résultante ${\overrightarrow{R}}_{\text{syst. de forces}}$ étant «${\overrightarrow{M}}_{A^{\prime },\text{syst. de forces}}=$ ${\overrightarrow{M}}_{A,\text{syst. de forces}}+\overrightarrow{A^{\prime }A}\wedge {\overrightarrow{R}}_{\text{syst. de forces}}$»,

Modèle:Alon en déduit que le moment résultant vectoriel d’un couple est indépendant du point origine par rapport il est calculé soit «${\overrightarrow{M}}_{A^{\prime },\text{couple}}={\overrightarrow{M}}_{A,\text{couple}}$» ;

Modèle:Alpour le différencier des autres systèmes de forces de vecteur moment résultant dépendant du point origine, le vecteur moment $($résultant$)$ d’un couple est usuellement noté «$\overrightarrow{\mathrm{\Gamma }}$».

Modèle:AlRemarque : Comme cela a déjà été dit, un couple $($en tant que système de forces$)$ est un cas particulier de « torseur couple » introduit en complément dans le chap.$1$ de la leçon « Outils mathématiques pour la physique - bis (PCSI) », on peut donc lui attribuer, sans autre commentaire, les propriétés d'un torseur couple vues dans le chapitre précité soit, en particulier, la constance du moment du torseur en tout point de l'espace $\dots$

Équivalence d'un système de forces extérieures s'exerçant sur un solide : ensemble d'une force appliquée en un point et d'un couple

Modèle:AlConsidérant un solide $\left(S\right)$ et son système de forces exercées par son extérieur ${\left(\mathrm{\Sigma }\right)}_k$, de résultante «${\overrightarrow{R}}_{\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}$» et de moment résultant au point origine $A$ «${\overrightarrow{ℳ}}_{A,\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}$» $[$avec la notion $($hors programme de physique de P.C.S.I.$)$ de « torseur » introduite dans le chap.$1$ de la leçon « Outils mathématiques pour la physique - bis (PCSI) », l'ensemble des vecteurs résultante et moment résultant par rapport à un point origine quelconque $A$ d'un système de forces s'exerçant sur un système fermé de matière constituant les éléments de réduction en $A$ du torseur statique associé aux forces précitées s'exerçant sur ce système fermé de matière, on a donc «${𝒯}_{\text{stat},\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}={\left\{\begin{array}{c}{\overrightarrow{R}}_{\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}\\ {\overrightarrow{ℳ}}_{A,\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}\end{array}\right\}}_A$»$]$ et
Modèle:Alsachant que l'évolution spatiale d'un solide $($c'est-à-dire un système fermé indéformable$)$ ne dépend que des forces extérieures on en déduit que le système des forces extérieures exercées par ${\left(\mathrm{\Sigma }\right)}_k$ sur $\left(S\right)$ peut être remplacé par un système équivalent ayant même résultante ainsi que même moment résultant en n'importe quel point origine :

Modèle:AlSystème équivalent au système de forces extérieures que$\underset{\_}{({\mathrm{\Sigma }}_k)}$exerce sur$\underset{\_}{(S)}$ : $\succ$une « force unique ${\overrightarrow{R}}_{\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}$ appliquée en $A$» et
Modèle:AlModèle:Transparent$\succ$un couple de moment «$\overrightarrow{\mathrm{\Gamma }}={\overrightarrow{ℳ}}_{A,\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}$» :
Modèle:AlModèle:Transparent$▸$justification : le moment du système de forces exercées par ${\left(\mathrm{\Sigma }\right)}_k$ sur $\left(S\right)$ au point origine $A^{\prime }$ quelconque distinct de $A$ s'écrivant «${\overrightarrow{ℳ}}_{A^{\prime },\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}=$ ${\overrightarrow{ℳ}}_{A,\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}+\overrightarrow{A^{\prime }A}\wedge {\overrightarrow{R}}_{\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}$» est effectivement identique
Modèle:AlModèle:Transparentà la somme du moment du couple «$\overrightarrow{\mathrm{\Gamma }}={\overrightarrow{ℳ}}_{A,\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}$» $($1^er terme du 2^ème membre$)$ et du moment de la force ${\overrightarrow{R}}_{\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}$ appliquée en $A$ «${\overrightarrow{ℳ}}_{A^{\prime }}\left[{\overrightarrow{R}}_{\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}\right]=\overrightarrow{A^{\prime }A}\wedge {\overrightarrow{R}}_{\left(S\right)\leftarrow {\left(\mathrm{\Sigma }\right)}_k}$» Modèle:Nobr terme du 2^ème membre$)$.

Notion de « liaison pivot », propriété de son moment

Modèle:AlUne « liaison pivot » est mise en œuvre lors du mouvement d'un 1^er solide sur un 2^ème solide, dans le but de restreindre le mouvement relatif à un mouvement de rotation autour d'un axe fixe du référentiel lié au 2^ème solide.

Définition d'une « liaison pivot »

Modèle:AlUne « liaison pivot » d'axe $Oz$ restreint les possibilités de mouvement du « rotor » $($solide tournant$)$ à une rotation d’axe $Oz$ par rapport au « stator » $($solide par rapport auquel se fait la rotation$)$ ;

Modèle:Alon suppose, dans ce paragraphe, la liaison pivot « géométriquement idéale » c'est-à-dire qu'elle assure un guidage parfait en rotation autour de l'axe de liaison $Oz$ en bloquant toute translation le long de cet axe ;

Modèle:Alla liaison pivot est entièrement définie par la direction et la position de l'axe $Oz$ qui doit être systématiquement représenté tout schéma ;

Modèle:Alla liaison pivot est la liaison la plus « commune » des systèmes mécaniques.

Réalisation pratique d'une « liaison pivot »

Schéma d'une liaison pivot $($idéale$)$ d'axe $z^{\prime }z$ pour laquelle les translations sont bloquées ainsi que les rotations suivant les axes $\perp$ à $z^{\prime }z$ ;
Modèle:Alle cylindre sur lequel tourne le rotor et qui matérialise l'axe de la liaison pivot exerce un système de forces sur le rotor équivalent à
Modèle:Al$\succ$une résultante $\overrightarrow{R}(R_x,R_y,R_z)$, appliquée en $A$, de direction quelconque, s'adaptant aux actions exercées sur le rotor de façon à supprimer toute translation de ce dernier et
Modèle:Al$\succ$un couple $\overrightarrow{\mathrm{\Gamma }}({\mathrm{\Gamma }}_x,{\mathrm{\Gamma }}_y,{\mathrm{\Gamma }}_z=0)$, de direction $\perp$ à $z^{\prime }z$, s'adaptant aux actions exercées sur le rotor de façon à supprimer toute rotation de ce dernier autre que celle autour de $z^{\prime }z$ laquelle, en absence de frottements, se traduit par ${\mathrm{\Gamma }}_z=0$

Éclaté d'un roulement à billes :
Modèle:Al 1. bague extérieure
Modèle:Al 2. bille
Modèle:Al 3. cage
Modèle:Al 4. chemin de la bille
Modèle:Al 5. bague intérieure

Roulement à aiguilles

Modèle:AlLa solution technique la plus courante pour réaliser une « liaison pivot » consiste à emboîter deux cylindres de même axe et à réaliser des butées pour empêcher les cylindres de coulisser le long de leur axe commun Modèle:Nobr schéma ci-dessus$)$ ;

Modèle:Alle contact entre les deux cylindres conduit à l'existence de frottements solides que l'on réduit à l’aide

• d'une « lubrification » ou,
• en utilisant
  Modèle:Transparentdes roulements « à billes » $($voir éclaté à gauche$)$ ou
  Modèle:Transparent« à aiguilles » $($voir photo à droite$)$,
  l'utilisation de roulements étant toujours préférable.

Action d’une « liaison pivot », cas d’une « liaison pivot idéale » d’axe Az

Modèle:AlSi on étudie les forces de contact assurant le guidage en rotation du rotor sur le cylindre d'axe $z^{\prime }z$ au niveau de la coupe $\left(BC\right)$ du 1^er schéma du paragraphe précédent « réalisation pratique d'une liaison pivot », on constate qu'elles sont réparties tout au long de la surface de contact et $\perp$ à celle-ci dans la mesure où « les frottements solides $($ou fluides$)$ sont supposés négligeables », elles coupent donc l'axe de rotation $z^{\prime }z$ et par suite le moment scalaire relativement à l'axe$\underset{\_}{z^{\prime }z}$de ces forces de contact assurant le guidage en rotation du rotor sur le cylindre d'axe$\underset{\_}{z^{\prime }z}$est nul.

Modèle:AlRemarque : Il y a d'autres forces de contact entre le rotor et le cylindre d'axe $z^{\prime }z$ sur lequel le rotor tourne, ce sont

• celles assurant l'absence de translation du rotor le long des trois axes $(x^{\prime }x,y^{\prime }y,z^{\prime }z)$ du cylindre, ces forces ayant une résultante s'adaptant à toute action pouvant entraîner une translation avec un moment $($vectoriel$)$ résultant nul en un point $A$ de l'axe $z^{\prime }z$ et
• celles assurant l'absence de basculement du rotor autour des deux axes $(x^{\prime }x,y^{\prime }y)$ du cylindre, ces forces ayant donc un moment $($vectoriel$)$ résultant au point $A$ de l'axe $z^{\prime }z$ de direction $\perp$ à l'axe $z^{\prime }z$ s'adaptant à toute action pouvant entraîner un basculement avec éventuellement une résultante non nulle de direction quelconque ;

Modèle:AlModèle:Transparentsi on considère le système de toutes les forces de contact assurant le guidage du rotor en rotation sur le cylindre d'axe

$z^{\prime }z$

, l'absence de translation du rotor relativement au cylindre ainsi que celle de basculement du rotor perpendiculairement au cylindre, ce système de forces étant de résultante

$($

vectorielle

$)$

«

$\overrightarrow{R}(R_x,R_y,R_z)$

» et de moment résultant

$($

vectoriel

$)$

en un point

$A\in z^{\prime }z$

«

${\overrightarrow{ℳ}}_A$ $({ℳ}_{A,x},{ℳ}_{A,y},{ℳ}_{A,z}=0)$

», est équivalent, d'après la propriété établie dans le paragraphe « équivalence d'un système de forces extérieures s'exerçant sur un solide : ensemble d'une force appliquée en un point et d'un couple » plus haut dans ce chapitre, au système composé

d'une force unique «$\overrightarrow{R}(R_x,R_y,R_z)$» appliquée en $A$ et
d'un couple de moment vectoriel «$\overrightarrow{\mathrm{\Gamma }}={\overrightarrow{ℳ}}_A({\mathrm{\Gamma }}_x={ℳ}_{A,x},{\mathrm{\Gamma }}_y={ℳ}_{A,y},{\mathrm{\Gamma }}_z={ℳ}_{A,z}=0)$»,

Modèle:AlModèle:Transparent« la nullité de ${\mathrm{\Gamma }}_z$» caractérisant une « liaison pivot idéale »,
Modèle:AlModèle:Transparent« la présence de frottements » même faibles $($la liaison pivot est alors « non idéale »$)$ correspondant à «${\mathrm{\Gamma }}_z<0$».

Notions simples sur les « moteurs ou freins » dans les dispositifs rotatifs, présence d’un « stator » exerçant un couple sur le « rotor »

Généralités

Modèle:Al$\succ$ Dans un dispositif rotatif autour d'un axe fixe $Oz$ du référentiel d'étude $ℛ$, il y a

• un solide tournant autour de $Oz$ appelé « rotor » et
• un solide fixe dans $ℛ$ appelé « stator »,

Modèle:Alle rotor étant usuellement en « liaison pivot » relativement au stator ;

Modèle:Al$\succ$ le dispositif rotatif peut être

• « moteur », dans ce cas le stator doit exercer un couple moteur sur le rotor pour que « celui-ci soit entraîné » ou
• « résistif » $($il agit donc en « frein »$)$, dans ce cas le stator doit exercer un couple résistif sur le rotor pour que « celui-ci ne s'emballe pas » $\dots$

Cas du moteur

Modèle:AlLe dispositif rotatif est « moteur » dans la mesure où le stator exerce un couple moteur sur le rotor pour entraîner ce dernier lequel, à son tour, déploie une action motrice sur l'objet en interaction avec le rotor ;

Modèle:Alsi la liaison pivot entre stator et rotor est quasi-idéale $($c'est-à-dire telle que les frottements solides ou fluides soient négligeables$)$ et si le rotor est en rotation libre $($c'est-à-dire sans interaction avec un objet sur lequel il est censé agir$)$ le couple moteur que le stator doit exercer sur le rotor est quasi nul mais

Modèle:AlModèle:Transparent si le rotor déploie une action motrice sur une partie extérieure au système rotatif Modèle:Nobr alors dit « en charge »$)$, la partie soumise à l'action du rotor exerçant un couple résistant sur ce dernier, le stator doit appliquer sur le rotor un couple moteur de compensation sinon le rotor s’arrêtera $\{$en effet dans le cas où le moteur est utilisé pour entraîner une autre pièce mécanique en rotation, le rotor exerce un couple moteur sur cette pièce et, d'après le principe des actions réciproques, cette pièce exerce un couple résistant sur le rotor, pour maintenir le rotor en rotation $($et si possible uniforme$)$, il est nécessaire que le stator exerce un couple moteur de compensation sur le rotor, ce couple s'adaptant au couple résistant que la pièce mécanique en rotation exerce sur le rotor $[$couple moteur quasi nul en absence de pièce à entraîner Modèle:Nobr parle alors de fonctionnement à vide du moteur$)$ et de moment scalaire d’autant plus grand que l’inertie de la pièce à entraîner est grande $($on parle alors de fonctionnement en charge du moteur$\left)\right]\}$.

Cas du frein

Modèle:AlLe dispositif rotatif est « résistif » dans la mesure où le stator exerce un couple résistif sur le rotor pour que ce dernier « ne s'emballe pas » lequel, à son tour, déploie une action résistive sur l'objet en interaction avec le rotor $($ce qui est le but recherché lorsque le rotor doit avoir une action de « frein »$)$ ;

Modèle:Alsi la liaison pivot entre stator et rotor est quasi-idéale $($c'est-à-dire telle que les frottements solides ou fluides soient négligeables$)$ et si le rotor est en rotation libre $($c'est-à-dire sans interaction avec un objet sur lequel il est censé agir$)$ le couple résistif que le stator doit exercer sur le rotor est quasi nul mais

Modèle:AlModèle:Transparent si le rotor déploie une action résistive sur une partie extérieure au système rotatif $($comme c'est le but recherché par tout « frein », le rotor étant alors « en charge »$)$, la partie soumise à l'action du rotor exerçant un couple moteur sur ce dernier, le stator doit appliquer sur le rotor un couple résistif de compensation sinon le rotor s’emballera $\{$en effet dans le cas où le frein est utilisé pour ralentir une autre pièce mécanique en rotation, le rotor exerce alors un couple résistif sur cette pièce et, d'après le principe des actions réciproques, cette pièce exerce un couple motor sur le rotor, pour maintenir le rotor en rotation $($et si possible uniforme$)$, il est nécessaire que le stator exerce un couple résistif de compensation sur le rotor, ce couple s'adaptant au couple moteur que la pièce mécanique en rotation exerce sur le rotor $[$couple résistif quasi nul en absence de pièce à ralentir Modèle:Nobr parle alors de fonctionnement à vide du frein$)$ et de moment scalaire négatif de valeur absolue d’autant plus grande que l’inertie de la pièce à ralentir est grande $($on parle alors de fonctionnement en charge du frein$\left)\right]\}$.

Modèle:AlExemple du frein avant$\underset{\_}{(}$ou arrière$\underset{\_}{)}$d’une bicyclette entraînée dans une descente :
Modèle:Alle rotor étant la roue avant $($ou arrière$)$ et le stator le cadre de la bicyclette, on choisit le référentiel d’étude $ℛ$ lié au cadre de cette dernière ;
Modèle:Alle sol de la route descendante défile dans $ℛ$ vers l’arrière de plus en plus vite en absence de freinage $[$on peut dire que la vitesse de défilement de la route dans $ℛ$ s’emballe en absence de freinage$]$ et pour éviter cela il est nécessaire de ralentir le défilement de la route dans $ℛ$,
Modèle:Alla route descendante exerçant un couple moteur sur la roue $($rotor$)$, le cadre de la bicyclette $($stator$)$ doit exercer un couple résistant sur la roue Modèle:Nobr ce qui est réalisé à l’aide de l’action des patins du frein s’appuyant sur la roue $\dots$