Fonctions d'une variable réelle/Développements limités

Modèle:Chapitre Dans tout ce chapitre, $f$ est une fonction définie sur un intervalle $I$ et continue en un point $a\in I$ et $n$ est un entier naturel.

Définition

La fonction cosinus et son développement limité d'ordre 4 au voisinage de 0.

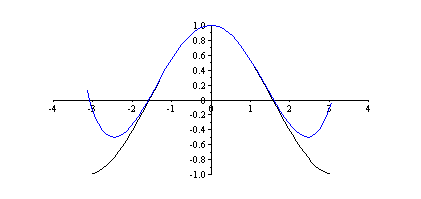
L'idée à retenir est qu'un développement limité est une approximation polynomiale au voisinage du point où il est effectué : l'image le montre bien. Modèle:Clr

Formules de Taylor

Modèle:Wikipédia Nous exposons ici trois formules de Taylor :

Remarque

Pour démontrer ce théorème, on utilise celui d'intégration terme à terme Modèle:Infra. Ces deux théorèmes se généralisent aux fonctions d'un espace vectoriel normé dans un autre : voir Calcul différentiel/Théorèmes utiles#Développement limité.

La formule de Taylor-Young est à usage local (du fait de la présence du $o((x-a{)}^n)$).

Les autres formules de Taylor sont à usage global.

Elles permettent notamment de préciser la valeur du « reste » de la formule de Taylor-Young :

La formule de Taylor-Lagrange et son corollaire immédiat, l'inégalité de Taylor-Lagrange, sont des généralisations respectives du théorème des accroissements finis et de l'inégalité des accroissements finis (voir Fonctions d'une variable réelle/Dérivabilité).

Modèle:Théorème (Si $x<a$, on a un énoncé analogue en remplaçant $[a,x]$ par $[x,a]$ et $]a,x[$ par $]x,a[$.) Modèle:Démonstration déroulante

Développements limités des fonctions usuelles en zéro

On a alors les développements limités des fonctions usuelles, directement (ou presque) avec la formule de Taylor-Young :

• le développement limité à l’ordre $n$ d'une fonction polynomiale est la troncature de cette fonction à l’ordre $n$ ;
• ${\mathrm{e}}^x=1+x+\frac{x^2}{2!}+\cdots +\frac{x^n}{n!}+o(x^n)=\sum _{k=0}^n\frac{x^k}{k!}+o(x^n)$
• $\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots +\frac{(-1{)}^n{x}^{2n+1}}{(2n+1)!}+o(x^{2n+1})=\sum _{k=0}^n\frac{(-1{)}^k{x}^{2k+1}}{(2k+1)!}+o(x^{2n+1})$
• $\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots +\frac{(-1{)}^n{x}^{2n}}{(2n)!}+o(x^{2n})=\sum _{k=0}^n\frac{(-1{)}^k{x}^{2k}}{(2k)!}+o(x^{2n})$
• $(1+x{)}^a=1+ax+\frac{a(a-1)x^2}{2!}+\frac{a(a-1)(a-2)x^3}{3!}+\cdots +\frac{a(a-1)\cdots (a-n+1)x^n}{n!}+o(x^n)=\sum _{k=0}^n\frac{c_k{x}^k}{k!}+o(x^n)$
  avec $c_n=\prod _{i=0}^{n-1}(a-i)$ et $a\in ℝ\setminus \mathbb{N}$ (si $a\in \mathbb{N}$, c’est un polynôme…) ;
  • Cas particulier : $a=-1$ :
    $\frac{1}{1+x}=(1+x{)}^{-1}=1-x+x^2-x^3+x^4+\cdots +(-1{)}^n{x}^n+o(x^n)$
    et $\frac{1}{1-x}=(1-x{)}^{-1}=1+x+x^2+x^3+x^4+\cdots +x^n+o(x^n)$.

Remarque : On trouvera parfois dans d'autres sources des listes (beaucoup) plus longues de développements limités à connaître. Cependant, ceux présentés ci-dessus suffisent dans la pratique ; les exemples ci-dessous montrent comment obtenir d'autres développements limités à partir de ceux-ci.

Propriétés des développements limités

Dérivation et intégration terme à terme

Remarque

Ce théorème d'« intégration » (plus exactement : de primitivation) terme à terme s'étend aux fonctions d'un espace vectoriel normé dans un autre : voir Calcul différentiel/Théorèmes utiles#Développement limité.

Pourquoi ne peut-on pas dériver un développement limité terme à terme comme on peut le faire pour une primitive ?

Pour comprendre, on peut prendre l'exemple classique de $f(x)=x^2\sin \frac{1}{x}$, prolongée par $f(0)=0$. Cette fonction admet un développement limité d'ordre $1$ en $0$ mais $f^{\prime }$ n'a pas de limite en $0$ donc pas de développement limité en $0$ (même à l'ordre $1-1=0$).

L'idée est qu'en dérivant, on « perd (au moins un peu) la régularité » de la fonction (si $f$ est de classe ${𝒞}^k$, alors $f^{\prime }$ est de classe ${𝒞}^{k-1}$) et rien n'assure que si $f$ admet un développement limité à l'ordre $n$ alors $f^{\prime }$ en admet un, même à l'ordre $n-1$.

Par contre, on « gagne en régularité » en intégrant donc on peut être sûr de l’existence du développement limité de $F$.

Exemples

Les exemples qui suivent illustrent quelques méthodes de calcul des développements limités souvent utilisées et montrent comment, grâce à ces propriétés, on peut obtenir de nouveaux développements limités.

Voyez aussi les exercices sur les développements limités.

Applications : calculs de limites et étude locale d'une fonction

La limite d'une fonction en un point $a$ est égale à celle de son développement limité en $a$.

Mais il y a nettement mieux : le développement limité donne une « vision » du comportement de la fonction au voisinage du point $a$. En particulier, pour trouver une équation de tangente (ou d'asymptote, voir le paragraphe suivant) en $a$ à la courbe de la fonction, il suffit de prendre les termes de degré $0$ et $1$ du développement limité.
Le signe des termes d'ordre supérieur donne la position de la courbe par rapport à cette tangente (ou asymptote).

Développements limités généralisés

Ce sont des développements limités en $+\mathrm{\infty }$ ou en $-\mathrm{\infty }$. On les déduit de ceux en $0$ par un changement de variable $h=\frac{1}{x}$.