Transformées de Fourier usuelles

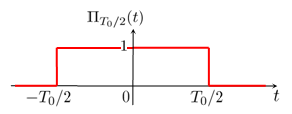
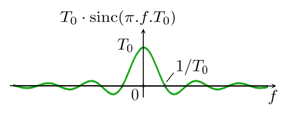
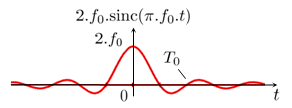
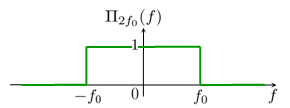
Modèle:Acquisition de bibliothèqueLe tableau qui suit présente les fonctions usuelles et leur transformée dans le cas où on utilise la convention la plus fréquente conforme à la définition mathématique.

Transformée de Fourier	Transformée de Fourier inverse

Quelques unes des démonstrations sont données dans le chapitre : Série et transformée de Fourier en physique/Fonctions utiles.

Fonction	Représentation temporelle	Représentation fréquentielle
Pic de Dirac	$\delta (t)$	$1$
Pic de Dirac décalé de $t_0$	${\delta }_{t_0}(t)=\delta (t-t_0)$	${\mathrm{e}}^{-\mathrm{j}.2\pi .f.t_0}$
Peigne de Dirac $T_e=\frac{1}{f_e}$	${\mathrm{I}\mathrm{I}\mathrm{I}}_{T_e}(t)$	${\mathrm{I}\mathrm{I}\mathrm{I}}_{f_e}(f)$
Fonction porte de largeur $T_0$	${\mathrm{\Pi }}_{T_0/2}(t)$	$T_0\cdot \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}(\pi .f.T_0)$
Constante	$1$	$\delta (f)$
Exponentielle complexe	${\mathrm{e}}^{\mathrm{j}.2\pi .f_0.t}$	$\delta (f-f_0)$
Sinus	$\sin (2\pi .f_0.t+{\phi }_0)$	$\frac{1}{2.\mathrm{j}}\cdot ({\mathrm{e}}^{\mathrm{j}.{\phi }_0}\cdot \delta (f-f_0)-{\mathrm{e}}^{-\mathrm{j}.{\phi }_0}\cdot \delta (f+f_0))$
Cosinus	$\cos (2\pi .f_0.t+{\phi }_0)$	$\frac{1}{2}\cdot ({\mathrm{e}}^{\mathrm{j}.{\phi }_0}\cdot \delta (f-f_0)+{\mathrm{e}}^{-\mathrm{j}.{\phi }_0}\cdot \delta (f+f_0))$
Sinus cardinal	$2\cdot f_0\cdot \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}(2\pi .f_0.t)$	${\mathrm{\Pi }}_{2f_0}(f)$

Modèle:ExpReprésentation du spectre d'amplitude