Série et transformée de Fourier en physique/Fonctions utiles
Certaines fonctions sont fréquemment utilisées en physique du fait de leur simplicité ou de leur intérêt pratique. Quelques unes d'entres elles sont rassemblées dans la [[../Fiche/Transformées de Fourier usuelles/|fiche mémoire]]. Ce chapitre les présente un peu plus en détails.
Pic de Dirac
La distribution de Dirac à l'instant correspond au pic de Dirac décalé dans le temps :
- .
Sa transformée de Fourier a la même amplitude mais présente un retard de phase :
- .
Peigne de Dirac

Modèle:Wikipédia La distribution peigne de Dirac est une somme de distributions de Dirac espacées de :
- .
Dans le cadre du traitement du signal numérique est la période d’échantillonnage. Modèle:Clr
Décomposition en séries de Fourier

Puisque cette distribution est périodique, on peut la développer en série de Fourier :
- .
Modèle:Démonstration déroulante
On peut en déduire que la transformée de Fourier d'un peigne de Dirac est un peigne de Dirac :
- .
Application aux signaux échantillonnés
est le signal échantillonné à la période du signal : .
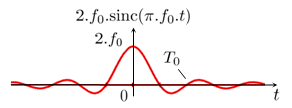
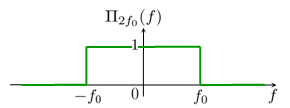
Fonction porte
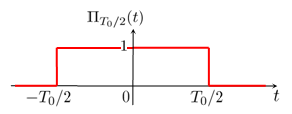
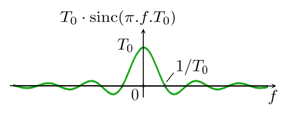
Modèle:Clr Modèle:Démonstration déroulante
Fonction porte convoluée par un peigne de Dirac


Dans de nombreux cas pratiques, l'échantillonnage ne peut pas être considéré instantané. La fonction d'échantillonnage n'est alors plus un peigne de Dirac mais une somme de portes de largeur espacée d'une durée : elle correspond à la convolution d'une porte par un peigne de Dirac de période .
Fonction exponentielle complexe
Modèle:Démonstration déroulante
Fonction sinus et cosinus


Les fonctions sinus et cosinus sont indispensables car elles décrivent un signal le plus simple qui soit : ce dernier ne comporterait alors qu'une seule fréquence (positive).
Modèle:Clr Modèle:Démonstration déroulante
Modèle:Clr Modèle:Démonstration déroulante
Fonction sinus cardinal