Outils mathématiques pour la physique (PCSI)/Fonctions trigonométriques inverses
Rappel et additif sur les fonctions trigonométriques directes
Modèle:Alle domaine de définition est « pour les deux 1ères », « pour tangente » et « pour cotangente » ;
Modèle:Al« les deux 1ères sont -périodiques » et « les deux suivantes -périodiques » ;
Modèle:Alelles sont « continues et dérivables sur leur domaine de définition », leurs dérivées étant respectivement :
Modèle:AlModèle:Transparent«»[2],
Modèle:AlModèle:Transparent«» [2],
Modèle:AlModèle:Transparent«» [3] et
Modèle:AlModèle:Transparent«» [4] ;
Modèle:Alles tracés sont rappelés ci-dessous [5].
-
Tracé du graphe de et choix de son domaine d'inversabilité
-
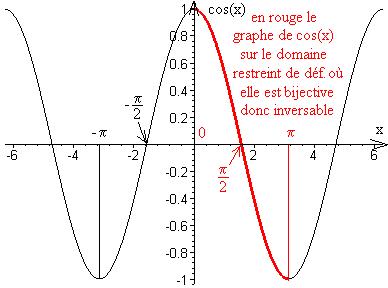
Tracé du graphe de et choix de son domaine d'inversabilité
-
Tracé du graphe de et choix de son domaine d'inversabilité
-
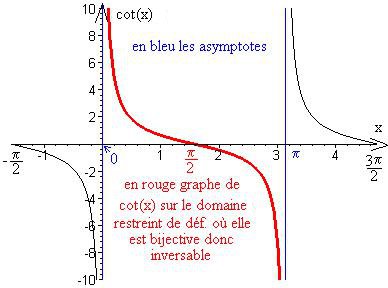
Tracé du graphe de et choix de son domaine d'inversabilité
Condition pour qu'une fonction soit inversible, notion de fonction bijective
Définition de fonction bijective
Modèle:AlUne fonction est « bijective » si et seulement si « tout élément du domaine des valeurs a un et un seul antécédent du domaine de définition » c.-à-d. encore « si tout élément du domaine des valeurs est image d'exactement un élément du domaine de définition » ;
Modèle:Alune fonction bijective est à la fois « injective » [6] et « surjective » [7].
Condition pour qu'une fonction soit inversible
Modèle:AlPour qu'une fonction soit inversible elle doit être bijective[8] :
- si l'ensemble de départ est son domaine de définition et l'ensemble d'arrivée son domaine de valeurs, elle est nécessairement surjective[7] car tout élément du domaine de valeurs a au moins un antécédent dans le domaine de définition mais elle peut ne pas être injective[6] car des éléments du domaine des valeurs peuvent avoir plusieurs antécédents dans le domaine de définition c'est le cas de la fonction « sinus » appliquant dans
- si la fonction n'est pas injective[6] quand on considère son domaine de définition complet cas de la fonction « sinus », on peut restreindre le domaine de définition en maintenant le domaine des valeurs pour que la « fonction restreinte » devienne injective[6]Modèle:,[9], tout en restant surjective[7]Modèle:,[10].
Fonction inverse de la fonction sinus : fonction arcsinus
Modèle:Al« Pour que la fonction soit inversible il faut restreindre son domaine de définition » de façon à ce que sa fonction restreinte soit « bijective »[8] et
Modèle:AlModèle:Transparentceci est réalisé pour un « domaine de définition restreint à » ;
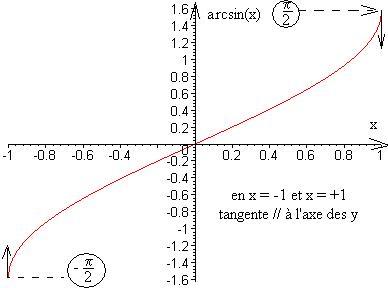
Modèle:Al«fonction inverse de», pour cette dernière le « domaine de définition étant restreint à » et
Modèle:AlModèle:Transparentle « domaine des valeurs restant » on en déduit
Modèle:AlModèle:Transparent« le domaine de définition de la fonction » et
Modèle:AlModèle:Transparent« son domaine de valeurs » ;
Modèle:Altracé du graphe de la fonction : voir ci-contre
Modèle:AlModèle:Transparentle graphe de est le symétrique de celui de par rapport à la 1ère diagonale ;
Modèle:Alon observe que la fonction est «»,
Modèle:AlModèle:Transparent« continue sur » et
Modèle:AlModèle:Transparent« dérivable sur », sa dérivée valant «» ;
Modèle:Aljustification de la dérivée : on démontre ce résultat en inversant la fonction « » [11], puis
Modèle:AlModèle:Transparenten différenciant la fonction inversée, ce qui donne «» dont on tire
Modèle:AlModèle:Transparent« à condition que ne soit pas nul », « réalisé si ou »[12],
Modèle:AlModèle:Transparenton termine en éliminant au profit de avec «» [13] soit « dont on déduit » ;
Modèle:Alconséquence : on déduit de cette expression de dérivée de la fonction qu'« une primitive de est ».
Fonction inverse de la fonction cosinus : fonction arccosinus
Modèle:Al« Pour que la fonction soit inversible il faut restreindre son domaine de définition » de façon à ce que sa fonction restreinte soit « bijective »[8] et
Modèle:AlModèle:Transparentceci est réalisé pour un « domaine de définition restreint à » ;

Modèle:Al«fonction inverse de», pour cette dernière le « domaine de définition étant restreint à » et
Modèle:AlModèle:Transparentle « domaine des valeurs restant » on en déduit
Modèle:AlModèle:Transparent« le domaine de définition de la fonction » et
Modèle:AlModèle:Transparent« son domaine de valeurs » ;
Modèle:Altracé du graphe de la fonction : voir ci-contre
Modèle:AlModèle:Transparentle graphe de est le symétrique de celui de par rapport à la 1ère diagonale ;
Modèle:Alon observe que la fonction est «»,
Modèle:AlModèle:Transparent« continue sur » et
Modèle:AlModèle:Transparent« dérivable sur », sa dérivée valant «» ;
Modèle:Aljustification de la dérivée : on démontre ce résultat en inversant la fonction « » [14], puis
Modèle:AlModèle:Transparenten différenciant la fonction inversée, ce qui donne «» dont on tire
Modèle:AlModèle:Transparent« à condition
Modèle:AlModèle:Transparentque ne soit pas nul », « réalisé si ou »[15],
Modèle:AlModèle:Transparenton termine en éliminant au profit de avec «»[16] soit « dont on déduit » ;
Modèle:Alconséquence : on déduit de cette expression de dérivée de la fonction qu'« une primitive de est aussi ».
Fonction inverse de la fonction tangente : fonction arctangente
Modèle:Al« Pour que la fonction soit inversible il faut restreindre son domaine de définition » de façon à ce que sa fonction restreinte soit « bijective »[8] et
Modèle:AlModèle:Transparentceci est réalisé pour un « domaine de définition restreint à » ;

Modèle:Al«fonction inverse de», pour cette dernière le « domaine de définition étant restreint à » et
Modèle:AlModèle:Transparentle « domaine des valeurs restant » on en déduit
Modèle:AlModèle:Transparent« le domaine de définition de la fonction » et
Modèle:AlModèle:Transparent« son domaine de valeurs » ;
Modèle:Altracé du graphe de la fonction : voir ci-contre
Modèle:AlModèle:Transparentle graphe de est le symétrique de celui de par rapport à la 1ère diagonale ;
Modèle:Alon observe que la fonction est «»,
Modèle:AlModèle:Transparent« continue sur » et
Modèle:AlModèle:Transparent« dérivable sur », sa dérivée valant «» ;
Modèle:Aljustification de la dérivée : on démontre ce résultat en inversant la fonction « » [17], puis
Modèle:AlModèle:Transparenten différenciant la fonction inversée, ce qui donne «»
Modèle:AlModèle:Transparent«»,
Modèle:AlModèle:Transparenton termine en éliminant au profit de avec «» soit « dont on déduit » ;
Modèle:Alconséquence : on déduit de cette expression de dérivée de la fonction qu'« une primitive de est ».
Fonction inverse de la fonction cotangente : fonction arccotangente
Modèle:AlRemarque préliminaire : La fonction étant très peu utilisée par rapport à la fonction , il en est de même de leur fonction inverse, quasiment jamais utilisée par rapport à ,
Modèle:AlModèle:Transparentla fonction suffisant amplement[18].
Modèle:Al« Pour que la fonction soit inversible il faut restreindre son domaine de définition » de façon à ce que sa fonction restreinte soit « bijective »[8] et
Modèle:AlModèle:Transparentceci est réalisé pour un « domaine de définition restreint à » ;

Modèle:Al«fonction inverse de», pour cette dernière le « domaine de définition étant restreint à » et
Modèle:AlModèle:Transparentle « domaine des valeurs restant » on en déduit
Modèle:AlModèle:Transparent« le domaine de définition de la fonction » et
Modèle:AlModèle:Transparent« son domaine de valeurs » ;
Modèle:Altracé du graphe de la fonction : voir ci-contre
Modèle:AlModèle:Transparentle graphe de est le symétrique de celui de par rapport à la 1ère diagonale ;
Modèle:Alon observe que la fonction est «»,
Modèle:AlModèle:Transparent« continue sur » et
Modèle:AlModèle:Transparent« dérivable sur », sa dérivée valant «» ;
Modèle:Aljustification de la dérivée : on démontre ce résultat en inversant la fonction « » [19], puis
Modèle:AlModèle:Transparenten différenciant la fonction inversée, ce qui donne «»
Modèle:AlModèle:Transparent«»,
Modèle:AlModèle:Transparenton termine en éliminant au profit de avec «» soit « dont on déduit » ;
Modèle:Alconséquence : on déduit de cette expression de dérivée de la fonction qu'« une primitive de est aussi ».
Simplification de fonction composée de grandeurs trigonométriques directe et inverse
Modèle:AlNous nous proposons de simplifier des expressions du genre «» ou «»[20]
Présentation de la méthode de simplification sur le premier exemple
Modèle:AlSoit à simplifier «» :
Modèle:AlPosant «», on cherche donc à « évaluer en fonction de »[21] ;
Modèle:Al« l'inversion de conduit à », avec « dont on déduit » ;
Modèle:Alil reste alors à utiliser le lien entre « ce qu'on cherche à évaluer
» et « ce qu'on connaît
» par
Modèle:AlModèle:Transparent«
» dont on tire «
» et comme
est
,
Modèle:AlModèle:Transparent«
» soit, avec
, «
» ou finalement
Développement de la méthode de simplification sur le deuxième exemple
Modèle:AlSoit à simplifier «» :
Modèle:AlPosant «», on cherche donc à « évaluer en fonction de »[22] ;
Modèle:Al« l'inversion de conduit à », avec «», « étant de signe quelconque » mais « étant quant à elle » ;
Modèle:Alil reste alors à utiliser le lien entre « ce qu'on cherche à évaluer » et « ce qu'on connaît » soit
Modèle:AlModèle:Transparent«»,
Modèle:AlModèle:Transparent s'exprimant en fonction de par «» ou, avec ,
Modèle:AlModèle:Transparent«» d'où
» soit, avec
, «
» ou finalement
Notes et références
- ↑ Cette dernière étant très peu utilisée.
- ↑ 2,0 et 2,1 Cette dernière expression peut se déduire soit, en en prenant la partie imaginaire respectivement la partie réelle et sachant que la dérivée de la partie imaginaire respectivement de la partie réelle est la partie imaginaire respectivement de la partie réelle de la dérivée, la dernière expression énoncée concernant la dérivée de ou de .
- ↑ On dérive comme un quotient et on obtient soit, en utilisant , d'une part, et d'autre part en remplaçant par et en distribuant le dénominateur ; ces deux expressions sont à connaître.
- ↑ La fonction cotangente est liée à la fonction tangente par ; du caractère de la fonction tangente sur les intervalles continus où elle est définie, et donc de la positivité de sa dérivée, on en déduit que la fonction cotangente est sur les intervalles continus où elle est définie et que sa dérivée est négative d'où le signe «» précédant ;
Modèle:Alon établit l'expression de la dérivée en dérivant comme un quotient et on obtient ou, avec , d'une part, et d'autre part en réintroduisant et en distribuant le dénominateur on obtient ; ce résultat est beaucoup moins important que le précédent. - ↑ On remarque que les fonctions « sinus », « tangente » et « cotangente » sont impaires, alors que la fonction « cosinus » est paire.
- ↑ 6,0 6,1 6,2 et 6,3 Une fonction est injective si tout élément du domaine des valeurs a au plus un antécédent du domaine de définition ; la fonction « sinus » appliquant dans n'est pas injective car tout élément de possède une infinité d'antécédents.
- ↑ 7,0 7,1 et 7,2 Une fonction est surjective si tout élément du domaine des valeurs a au moins un antécédent du domaine de définition ; la fonction « sinus » appliquant dans est surjective car tout élément de possède au moins un antécédent ;
Modèle:Alsi l'ensemble de départ est le domaine de définition et l'ensemble d'arrivée le domaine des valeurs, une fonction est nécessairement surjective mais
Modèle:Alsi l'ensemble de départ est restreint en maintenant l'ensemble d'arrivée confondu avec le domaine de toutes les valeurs possibles, par exemple la fonction sinus considérée comme appliquant dans , l'application peut ne pas être surjective et c'est le cas sur l'exemple de l'application sinus appliquant dans non surjective car aucun élément de n'a d'antécédent dans . - ↑ 8,0 8,1 8,2 8,3 et 8,4 Voir le paragraphe « définition de fonction bijective » plus haut dans ce chapitre.
- ↑ La restriction du domaine de définition doit être telle que tout élément du domaine des valeurs ait au plus un antécédent dans le domaine restreint : par exemple la fonction « sinus » restreinte au domaine de définition , l'ensemble d'arrivée restant .
- ↑ Attention à ne pas trop restreindre le domaine de définition de façon qu'il n'existe aucun élément du domaine des valeurs n'ayant plus d'antécédent dans le domaine de définition restreint :
Modèle:Alpar exemple la fonction « sinus » restreinte au domaine de définition , l'ensemble d'arrivée restant , est certes injective car tout élément de a au plus un antécédent dans en effet l'antécédent existe et est unique si l'élément d'arrivée et l'antécédent n'existe pas si l'élément d'arrivée mais n'est plus surjective Modèle:Nobr élément de n'ayant d'antécédent dans . - ↑ L'équivalence n'étant correcte que pour et .
- ↑ D'où le domaine de dérivabilité de la fonction restreint à .
- ↑ est d'où égal à .
- ↑ L'équivalence n'étant correcte que pour et .
- ↑ D'où le domaine de dérivabilité de la fonction restreint à .
- ↑ est d'où égal à .
- ↑ L'équivalence n'étant correcte que pour et .
- ↑ Toutefois, pour des raisons de symétrie d'exposé, l'introduction est faite, mais vous ne l'utiliserez vraisemblablement jamais.
- ↑ L'équivalence n'étant correcte que pour et .
- ↑ Ces deux exemples quelconques devraient suffire pour présenter la méthode de simplification.
- ↑ Le fait de baptiser la fonction va permettre de préciser « son domaine de valeurs plus simplement », « son domaine de définition étant ».
- ↑ Le fait de baptiser la fonction va permettre de préciser « son domaine de valeurs plus simplement », « son domaine de définition étant ».