Thermodynamique des mélanges/Modèles de mélanges

Les systèmes réels sont souvent complexes à décrire et les physiciens simplifient le problème à résoudre en faisant des modèles qui tentent de représenter la réalité avec plus ou moins de précision.

Le modèle du gaz parfait

Les molécules d'un gaz parfait n'ont pas d'interactions entre elles et sont des objets ponctuels (sans volume).

• voir Théorie cinétique des gaz/Gaz parfait

Comme les molécules des gaz parfaits sont sans interactions (E_XY = 0), alors il n'y aura pas d'effet thermique lors du mélange ( Q_p = ΔH_mél = 0 ) et il n'y aura pas d’attraction ou de répulsion entre les molécules A et B ( V = V_{A (pur)} + V_{A (pur)} ou ΔV_mél = 0 ).

Pour un gaz parfait i , le potentiel chimique μ_i s'écrit:

${\mu }_i={\mu }_i^o+RT.Ln(\frac{P_i}{P^o})$

On modifie cette relation en introduisant la pression totale P_tot:

${\mu }_i={\mu }_i^o+RT.Ln(\frac{P_i.P_{tot}}{P^o.P_{tot}})={\mu }_i^o+RT.Ln(\frac{P_{tot}}{P^o})+RT.Ln(\frac{P_i}{P_{tot}})$

on pose ${\mu }_i^o+RT.Ln(\frac{P_{tot}}{P^o})={\mu }_i^{*}$

et comme

$\frac{P_i}{P_{tot}}=x_i$,

alors

${\mu }_i={\mu }_i^{*}+RT.Ln(x_i)$

pour un mélange parfait de gaz parfaits, on aura donc l'enthalpie libre G telle que:

$G=\sum _i{G}_i=\sum _i{n}_i.{\mu }_i=\sum _i{n}_i.({\mu }_i^{*}+RT.Ln(x_i))$

pour les gaz purs (séparés) on a :

$G_i^{pur}=n_i.{\mu }_i^{*}$

donc

$\mathrm{\Delta }{G}_{m\acute{e}l}=G-\sum _i{G}_i^{pur}=RT.(n_A.ln(x_A)+n_B.ln(x_B))<0$

On calcule l'entropie de mélange en dérivant:

$\mathrm{\Delta }{S}_{m\acute{e}l}=-(\frac{\partial \mathrm{\Delta }{G}_{m\acute{e}l}}{\partial T})=-R.\sum _i{n}_i.Ln(x_i)>0$

pour un mélange binaire A-B cela s'écrit:

$\mathrm{\Delta }{S}_{m\acute{e}l}=-R.(n_A.ln(x_A)+n_B.ln(x_B))$

et en divisant par n_tot, on obtient:

$\mathrm{\Delta }{s}_{m\acute{e}l}=-R.(x_A.ln(x_A)+x_B.ln(x_B))$

Définition du paramètre d'interaction λ

Si on note E_AA , E_BB et E_AB les énergies d'interaction entre deux molécules, alors on définit le paramètre d'interaction λ par:

$\lambda =Kte.(E_{AB}-\frac{1}{2}(E_{AA}+E_{BB}))$$$$$$$$$$$$$$$$$$$$$

Remarque = les énergies d'interaction entre deux molécules sont des grandeurs négatives ( E < 0 ).

• si λ = 0 avec E_AA = E_BB = E_AB = 0 ; alors c’est le modèle du mélange de gaz parfaits.
• si λ = 0 avec E_AA = E_BB = E_AB ≠ 0 et E_AB = 0,5(E_AA+E_BB) ; alors c’est le modèle du mélange idéal.
• si λ < 0 alors |E_AB| > 0,5|E_AA + E_BB| ; alors c’est un cas favorable pour la formation d'un mélange homogène.
• si λ > 0 alors |E_AB| < 0,5|E_AA + E_BB| ; alors c’est un cas défavorable pour la formation du mélange, on pourra donc faire le mélange dans certaines conditions mais on pourra aussi avoir parfois un phénomène de démixtion ( i.e. séparation en deux phases ).

Les mélanges réels

Les mélanges réels sont décrits par d'autres relations et l'on a pas en général la symétrie des courbes par rapport à x = 0,5 comme dans le cas des modèles précédents.

Les mélanges solides

Un mélange binaire solide homogène peut exister de deux manières:

• mélange solide de substitution
• mélange solide interstitiel

substitution

interstitiel

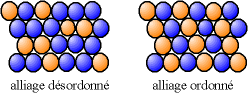
mélange solide de substitution

Les 2 solides doivent avoir la même structure cristalline et des rayon atomiques proches. Quand un des constituants est un métal, on parle d' alliages. Une substitution peut conduire, soit à un alliage désordonné, où les différents atomes occupent des positions aléatoires, soit à un alliage ordonné, où les atomes de différentes natures suivent une alternance régulière.

mélange solide interstitiel

Ici B doit avoir un rayon assez petit pour se glisser dans le réseau cristallin de A.

démixtion

On peut avoir formation de deux phases qui se répartissent dans le solide (cristallites).

Dans le cas des alliages, les phases à forte teneur en éléments d'alliage sont appelés « précipités ».

Les précipités sont souvent des alliages ordonnés, dits « intermétalliques ».

solution solide

On parle de solution solide quand un constituant est en excès (par exemple $x_A$ proche de 1).