Statique des fluides/Exercices/Aqueduc en surcharge

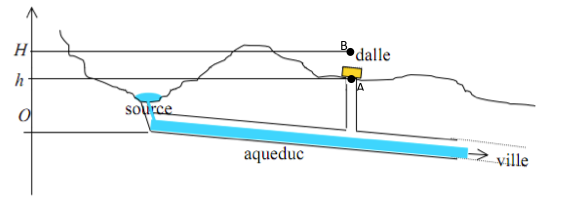
Les aqueducs romains souterrains étaient toujours munis de cheminée (comme il est représenté ci-­‐dessous) de manière à ce que l’eau reste aérée durant son drainage. Ces cheminées étaient en fait recouvertes d’une dalle en pierre percée d’un trou. En situation de fonctionnement normal, l’eau ne remplie que le fond de la cunette de l’aqueduc. Parfois la source, qui pouvait être une rivière, était en crû. L’eau remplissait alors complètement l’aqueduc jusqu’à remonter par les cheminées. On suppose ici que la crue est telle que la première dalle représentée sur le schéma est elle-­‐même expulsée par l’eau (le trou qui la perce n’étant pas suffisant pour permettre au flux de l’eau de ressortir assez vite à la surface). On note h la hauteur l’altitude du haut de la cheminée par rapport au niveau normal de la source, et H la hauteur atteinte au moment d’une crue. On note par ailleurs M la masse de la dalle et S la section de la cheminée.

1°) Déterminer, dans le cas où l’on négligerait totalement la vitesse de l’eau dans l’aqueduc (situation hydrostatique), la hauteur de crue au-­‐dessus de laquelle la dalle va se soulever (application numérique)

Nous voulons que : $P_{dalle}<P_{eau}$

La hauteur de crue au-­‐dessus de laquelle la dalle va se soulever signifie que l’on cherche quand : $P_{dalle}=P_{eau}$

Équation fondamentale de l’hydrostatique

$P_A+\rho gh=cte$
$P_B+\rho gH=cte$

$P_A+\rho gh=P_B+\rho gH$
$P_A=\rho g(H-h)+P_B$
$P_A=P_{atm}+\frac{Mg}{S}$

(On isole la dalle qui est en équilibre au point A. Après application du PFS on obtient $F_A=F_{atm}$ +Poids. On sait que P=F/S donc on obtient $P_A=P_{atm}+\frac{Mg}{S}$) $P_B=P_{atm}$ $\frac{Mg}{S}=\rho g(H-h)$ $H-h=\frac{M}{\rho S}$ $H=\frac{M}{\rho S}+h$

Si $H>\frac{M}{\rho S}+h$ alors la dalle se soulève AN : La dalle se soulève pour H > Modèle:Unité

2. Expliquer qualitativement si l’écoulement de l’eau qui se fait dans l’aqueduc aura pour effet d’augmenter ou de diminuer la hauteur de crue précédemment déterminée.

On a d’après l'équation de Bernoulli: $\frac{P{v}^2}{2}+\rho gz+P=cste$. On imagine deux cas en bas de la cheminée :

• Dans le premier cas, il n’y a pas de vitesse.

• Dans le deuxième cas (toujours à la même altitude) on a ρgz = constante. On imagine qu’il y ait un écoulement, donc une vitesse apparait. Pv2/2 augmente donc la pression P diminue.

On se place à l’intérieur de la cheminé, donc dans une situation hydrostatique. ρgz(haut cheminée) + P(haut cheminée) = ρgz(bas cheminée) + P( bas cheminée) Dans les deux cas ρgz(haut cheminée) = ρgz(bas cheminée) = cste.

Donc lorsque P(bas cheminée) diminue, P(haut cheminée) diminue proportionnellement. Ainsi la pression sur la dalle diminue. Donc il faudra une plus grande hauteur d’eau pour soulever la dalle.

Données : Masse de la dalle : M = Modèle:Unité Section de la cheminée : S = Modèle:Unité

Altitude du haut de la cheminée : h = Modèle:Unité

Masse volumique de l’eau : ρ = 1000 kg/m3

Accélération de la pesanteur : g