Signaux physiques (PCSI)/Exercices/Introduction au monde quantique : particule libre confinée 1D

Puits quantique à une dimension

Puits quantique à une dimension de profondeur finie

Diagramme du puits quantique à une dimension de profondeur $U_0$ et de largeur $𝔞$ suivant l'abscisse $x$

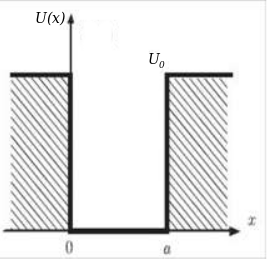
Modèle:AlOn considère une particule de masse $m$ décrite par une fonction d'onde $\underset{\_}{\psi }(x,t)$ évoluant dans un champ de force conservatif dérivant de l'énergie potentielle $U(x)$ dont le diagramme en fonction de l'abscisse $x$ de la position est représenté ci-contre.

Modèle:AlDans un 1^er temps, on considère un puits d'énergie potentielle de profondeur finie fixée à $U_0$ $($diagramme ci-contre$)$.

Écriture de l'équation de Schrödinger suivie par la particule

Modèle:AlÉcrire l'équation de Schrödinger à une dimension suivie par la particule.

Modèle:AlPréciser l'hamiltonien $\hat{\mathscr{H}}\left[\right]$ de la particule.

Signification physique de l'équation de Schrödinger suivie par la particule

Modèle:AlExpliquer physiquement la signification de l'équation de Schrödinger suivie par la particule ainsi que
Modèle:AlModèle:Transparentde la fonction d'onde $\underset{\_}{\psi }(x,t)$.

Conséquences de l'indépendance de l'hamiltonien de la particule relativement au temps

Modèle:AlSachant que l'hamiltonien $\hat{\mathscr{H}}\left[\right]$ de la particule est ici indépendant du temps, quelle forme prend la fonction $\underset{\_}{\psi }(x,t)$ ?

Modèle:AlEn déduire l'expression de l'équation de Schrödinger indépendante du temps.

Détermination de la solution générale de l'équation de Schrödinger dépendante du temps à partir des solutions de l'équation de Schrödinger indépendante du temps

Modèle:AlExpliquer pourquoi résoudre l'équation de Schrödinger indépendante du temps permet de déduire la solution générale de l'équation de Schrödinger dépendante du temps.

Forme générale de la partie spatiale de la fonction d'onde de la particule, solution de l'équation de Schrödinger indépendante du temps

Modèle:AlLe potentiel $U(x)$ étant constant par morceau, quelle forme générale prend la fonction $\underset{\_}{\mathrm{\Psi }}(x)$Modèle:, ?

Condition de quantification de l'énergie de la particule dans le cas où celle-ci est inférieure à la profondeur du puits

Modèle:AlIl est possible de montrer que, pour satisfaire l’équation de Schrödinger indépendante du temps, la fonction d'onde $\underset{\_}{\mathrm{\Psi }}(x)$ doit être continue ; de la même façon,

Modèle:AlModèle:Transparentdans la mesure où la discontinuité de l'énergie potentielle est finie, la dérivée de la fonction d’onde par rapport à l'abscisse de localisation $\frac{d\underset{\_}{\mathrm{\Psi }}}{dx}(x)$ est aussi Modèle:Nobr

Modèle:AlOn se place dans le cas où l'énergie $E$ est toujours inférieure à la profondeur du puits $U_0$.
Modèle:AlEn écrivant les conditions de continuités des morceaux de fonction d'ondeModèle:, aux barrières d'énergie potentielle ainsi que
Modèle:AlModèle:Transparentde leur dérivée spatiale 1^ère, puis
Modèle:AlModèle:Transparentla compatibilité de ces conditions, déterminer l'équation définissant la quantification de l'énergie puis
Modèle:AlModèle:Transparentla résoudre numériquement avec les données suivantes : $m=9,110^{-31}kg$, $𝔞=1nm\text{ou}2nm$, $U_0=1eV$ et on rappelle
Modèle:AlModèle:Transparentla constante réduite de Planck $\hslash =1,05610^{-34}J\cdot s$.

Partie spatiale de la fonction d'onde de la particule, solution de l'équation de Schrödinger indépendante du temps, dans le cas où l'énergie de la particule est inférieure à la profondeur du puits

Modèle:AlPréciser les formes que prennent alors les solutions dans les 3 zones de l'espace $]-\mathrm{\infty };0]$, $[0;𝔞]$ et $[𝔞;+\mathrm{\infty }[$ après les avoir normalisées globalement ?

Expression du taux de transmission à l'extérieur du puits à une distance a de chacune de ses frontières dans le cas où l'énergie de la particule est inférieure à la profondeur du puits

Modèle:AlDans le cas où l'énergie $E$ de la particule est $<$ à la profondeur $U_0$ du puits d'énergie potentielle large de $𝔞$, on définit le taux de transmission à l'extérieur du puits à une distance$𝔞$de chacune de ses frontières par «$T_{-𝔞\leftarrow 0}=\frac{|\mathrm{\Psi }(-𝔞){|}^2}{|\mathrm{\Psi }(0){|}^2}$ pour la transmission à gauche » et «$T_{𝔞\to 2𝔞}=\frac{|\mathrm{\Psi }(2𝔞){|}^2}{|\mathrm{\Psi }(𝔞){|}^2}$ pour la transmission à droite », $\mathrm{\Psi }(x)$ étant la fonction d'onde de la particule au point d'abscisse $x$ ;

Modèle:Alexplicitez, en fonction des données du problème, chacun des taux de transmission à l'extérieur du puits à une distance $𝔞$ de chacune de ses frontières et vérifiez qu'ils sont égaux ; commentez.

Modèle:AlFaire l'application numérique pour les deux largeurs de puits d'énergie potentielle précédemment introduites $𝔞=1nm$ et $𝔞=2nm$ $($on rappelle les autres valeurs numériques $m=9,110^{-31}kg$, $U_0=1eV$ et $\hslash =1,05610^{-34}J\cdot s$$)$ ; commentez.

Puits quantique à une dimension de profondeur infinie

Diagramme du puits quantique à une dimension de profondeur infinie et de largeur $𝔞$ suivant l'abscisse $x$

Modèle:AlDans un 2^ème temps, on considère un puits d'énergie potentielle $U(x)$ de profondeur infinie dont le diagramme en fonction de l'abscisse $x$ de la position est représenté ci-contre.

Partie spatiale de la fonction d'onde de la particule, solution de l'équation de Schrödinger indépendante du temps, en-deçà et au-delà des barrières

Modèle:AlQue devient alors la fonction d’onde $\underset{\_}{\mathrm{\Psi }}(x)$ en-deçà et au-delà des barrières ?

Modèle:Solution

Conditions aux limites que doit satisfaire la partie spatiale de la fonction d'onde de la particule, solution de l'équation de Schrödinger indépendante du temps à l'intérieur du puits

Modèle:AlEn utilisant le fait que la fonction d'onde $\underset{\_}{\mathrm{\Psi }}(x)$ doit être continue aux interfaces, c'est-à-dire en $x=0$ et $x=𝔞$, écrire les conditions aux limites que doit satisfaire $\underset{\_}{\mathrm{\Psi }}(x)$, solution de l'équation de Schrödinger indépendante du temps à l'intérieur du puits.

Condition de quantification de l'énergie de la particule à l'intérieur du puits d'énergie potentielle et expression de la partie spatiale de sa fonction d'onde, solution de l'équation de Schrödinger indépendante du temps

Modèle:AlEn imposant les conditions aux limites à la fonction d'onde $\underset{\_}{\mathrm{\Psi }}(x)$ solution de l'équation de Schrödinger indépendante du temps à l'intérieur du puits d'énergie potentielle,
Modèle:AlModèle:Transparentdéterminer la condition de quantification de l'énergie de la particule ;

Modèle:Alen utilisant la condition de normalisation de la fonction d'onde $\underset{\_}{\mathrm{\Psi }}(x)$, déterminer l'expression de $\underset{\_}{\mathrm{\Psi }}(x)$ à l'intérieur du puits d'énergie potentielle et

Modèle:AlModèle:Transparentcommenter les résultats.

Modèle:AlA.N. : on propose deux applications numériques pour lesquelles on rappelle la valeur de la constante de Planck $h=6,62610^{-34}J\cdot s$ :

• un électron $m=9,110^{-31}kg$ dans un puits d'énergie potentielle de profondeur infinie et de largeur $𝔞=1\text{Å}$,
• un proton $m=1,6710^{-27}kg$ dans un puits d'énergie potentielle de profondeur infinie et de largeur $𝔞=1fm$,

Modèle:AlModèle:Transparentdéterminer, dans chaque exemple, l'écart entre les énergies du niveau fondamental et le 1^er niveau excité puis

Modèle:AlModèle:Transparentcomparer à l'ordre de grandeur de l'écart de ces énergies dans un atome et dans un noyau.

Représentation graphique des trois premières fonctions d'onde et du carré de leurs modules

Modèle:AlDonner la représentation graphique des trois 1^ères fonctions d’onde et de leurs modules carrés $($c'est-à-dire à leurs densités linéiques de probabilité de présence associées$)$.

Interprétation physique des résultats précédents

Énergie fondamentale de la particule confinée dans ce puits et différence avec le résultat de mécanique classique

Modèle:AlQuelle est la plus basse énergie que puisse atteindre une particule confinée dans le puits ?

Modèle:AlEn quoi cette énergie est-elle différente de celle que l’on trouverait en mécanique classique ?

Justification de la différence précédente par inégalité spatiale de Heisenberg

Modèle:AlMontrer que la différence précédente est une conséquence directe de l'inégalité spatiale de HeisenbergModèle:,.

Signification physique de la partie spatiale de la fonction d'onde

Modèle:AlDiscuter la signification physique de la fonction d’onde ${\underset{\_}{\mathrm{\Psi }}}_n(x)$Modèle:, associée à l'énergie $E_n$ de la particule dans l'état de niveau $n\in {\mathbb{N}}^{*}$.

Évolution temporelle d'un état stationnaire

Modèle:AlExpliquer comment va évoluer temporellement un état stationnaire et en quoi cela justifie cette appellation.

Évolution temporelle d'un état correspondant à la superposition initiale de deux états stationnaires

Modèle:AlSoit $\underset{\_}{\psi }(x,0)=\underset{\_}{\alpha }{\underset{\_}{\mathrm{\Psi }}}_{n_1}(x)+\underset{\_}{\beta }{\underset{\_}{\mathrm{\Psi }}}_{n_2}(x)$ la fonction d'onde initiale associée à un état résultant d’une superposition quelconque de deux états stationnaires à l'instant initial $t=0$.
Modèle:AlModèle:TransparentComment va évoluer temporellement un tel état ?