Signaux physiques (PCSI)/Circuits électriques dans l'ARQS : associations de conducteurs ohmiques
Résistance équivalente de l'association série de deux conducteurs ohmiques, généralisation à l'association série de plus de deux conducteurs ohmiques
Association série de deux conducteurs ohmiques
Modèle:Théorème
Modèle:AlDémonstration : les conducteurs ohmiques étant en série sont traversés par la « même intensité de courant » et
Modèle:AlModèle:Transparentla tension aux bornes de l'association série des deux dipôles est égale à la somme des tensions et aux bornes de chaque dipôle, soit «» ;
Modèle:AlModèle:Transparentil reste à écrire que chaque dipôle est un conducteur ohmique par loi d'Ohm [2] en convention récepteur « et » puis
Modèle:AlModèle:Transparentà reporter ces expressions dans soit «» ;
Modèle:AlModèle:Transparentpour démontrer que l'association est équivalente à un conducteur ohmique « il faut observer que est à » et
Modèle:AlModèle:Transparentceci se vérifie en factorisant par dans l'expression de soit «»,
Modèle:AlModèle:Transparent« le cœfficient de proportionnalité étant alors la résistance équivalente ».
Modèle:AlCas particulier : « l'association série de deux conducteurs ohmiques de même résistance est un conducteur ohmique de résistance » [3].
Généralisation : association série de plus de deux conducteurs ohmiques
Modèle:Théorème
Modèle:AlDémonstration : les conducteurs ohmiques étant en série sont traversés par la « même intensité de courant » et
Modèle:AlModèle:Transparentla tension aux bornes de l'association série des n dipôles est égale à la somme des n tensions , , , , aux bornes de chaque dipôle, soit
Modèle:AlModèle:Transparent«» ;
Modèle:AlModèle:Transparentil reste à écrire que chaque dipôle est un conducteur ohmique par loi d'Ohm [2] en convention récepteur «, , , , » puis
Modèle:AlModèle:Transparentà reporter ces expressions dans soit «» ;
Modèle:AlModèle:Transparentpour démontrer que l'association est équivalente à un conducteur ohmique « il faut observer que est à » et
Modèle:AlModèle:Transparentceci se vérifie en factorisant par dans l'expression de soit «»,
Modèle:AlModèle:Transparent« le cœfficient de proportionnalité étant alors la résistance équivalente ».
Modèle:AlCas particulier : « l'association série de n conducteurs ohmiques de résistances identiques est un conducteur ohmique de résistance ».
Conductance équivalente de l'association parallèle de deux conducteurs ohmiques, résistance équivalente
Association parallèle de deux conducteurs ohmiques, conductance équivalente
Modèle:Théorème
Modèle:AlDémonstration : les conducteurs ohmiques étant en sont soumis à la « même tension » et
Modèle:AlModèle:Transparentl'intensité du courant traversant l'association parallèle des deux dipôles est égale à la somme des intensités et des courants traversant chaque dipôle, soit
Modèle:AlModèle:Transparent«» ;
Modèle:AlModèle:Transparentil reste à écrire que chaque dipôle est un conducteur ohmique par la 2ème forme de la loi d'Ohm [2] en convention récepteur « et » puis
Modèle:AlModèle:Transparentà reporter ces expressions dans soit «» ;
Modèle:AlModèle:Transparentpour démontrer que l'association est équivalente à un conducteur ohmique « il faut observer que est à » et
Modèle:AlModèle:Transparentceci se vérifie en factorisant par dans l'expression de soit «»,
Modèle:AlModèle:Transparent« le cœfficient de proportionnalité étant alors la conductance équivalente ».
Association parallèle de deux conducteurs ohmiques, résistance équivalente
Modèle:Théorème
Modèle:AlDémonstration : nous savons déjà que l'association parallèle de deux conducteurs ohmiques est un conducteur ohmique de conductance équivalente égale à la somme des conductances individuelles
Modèle:AlModèle:Transparent«» soit,
Modèle:AlModèle:Transparenten remplaçant les conductances individuelles par leurs valeurs de résistances associées, «» égale à « » d'où,
Modèle:AlModèle:Transparenten inversant, l'expression de «».
Modèle:AlCas particulier : « l'association de deux conducteurs ohmiques de même résistance est un conducteur ohmique de résistance » [3].
Conductance équivalente de l'association parallèle de plus de deux conducteurs ohmiques
Modèle:Théorème
Modèle:AlDémonstration : les conducteurs ohmiques étant en sont soumis à la même tension et
Modèle:AlModèle:Transparentl'intensité du courant traversant l'association parallèle des n dipôles est égale à la somme des intensités , , , , des courants traversant chaque dipôle, soit
Modèle:AlModèle:Transparent«» ;
Modèle:AlModèle:Transparentil reste à écrire que chaque dipôle est un conducteur ohmique par la 2ème forme de la loi d'Ohm [2] en convention récepteur , , , , puis
Modèle:AlModèle:Transparentà reporter ces expressions dans soit «» ;
Modèle:AlModèle:Transparentpour démontrer que l'association est équivalente à un conducteur ohmique « il faut observer que est à » et
Modèle:AlModèle:Transparentceci se vérifie en factorisant par dans l'expression de soit «»,
Modèle:AlModèle:Transparent« le cœfficient de proportionnalité étant alors la conductance équivalente ».
Modèle:AlRemarque : il n'y a aucune relation simple sur la résistance équivalente d'une association parallèle de plus de deux conducteurs ohmiques, on procède :
- par calcul de conductance équivalente et on inverse le résultat pour obtenir la résistance équivalente ou
- par itération « on associe d'abord deux conducteurs ohmiques pour déterminer la résistance équivalente » puis « on associe cette dernière avec un 3ème conducteur ohmique pour déterminer la nouvelle résistance équivalente » et « ainsi de suite jusqu'à épuisement des conducteurs montés en parallèle » [4].
Modèle:AlConseil : il est impératif de vérifier l'homogénéité des formules même si vous croyez faire des calculs sans erreurs
- un résultat du type pour la résistance équivalente de l'association parallèle de trois conducteurs ohmiques de résistance respective , et qui serait induit par Modèle:Nobr intuition à partir de celui de deux conducteurs ohmiques montés en parallèle
- ou encore du type
- ou du type
Modèle:AlModèle:Transparent« sont évidemment faux » puisque « non homogènes » [5].
Méthode générale de la détermination de la résistance équivalente d'un réseau dipolaire résistif, étude d'un exemple
Méthode à utiliser avant toute chose
Modèle:AlRemplacer les associations en série ou en parallèle de conducteurs ohmiques par le conducteur ohmique équivalent Le plus souvent ce sera la seule chose à faire car le réseau dipolaire purement résistif étudié sera une association de réseaux dipolaires rassemblant des conducteurs ohmiques uniquement montés en série ou en parallèle
Modèle:AlAttention : ne jamais perdre de vue les bornes entre lesquelles on cherche l'équivalence du réseau, toutes les erreurs que l'on peut rencontrer résultent de cet oubli [6].
Méthode à utiliser dans le cas où la résolution de la résistance équivalente par « association de conducteurs ohmiques en série ou en parallèle » n'aboutit pas
Modèle:AlIl convient avant toute chose de simplifier le réseau en remplaçant les associations en série ou et en parallèle de conducteurs ohmiques par le conducteur ohmique équivalent ; nous supposons que, malgré tout, il existe d'autres associations de conducteurs ohmiques que les associations en série ou en parallèle précédentes [7] qui empêchent d'obtenir un conducteur ohmique équivalent au réseau dipolaire initial.
Modèle:AlDans la mesure où le réseau dipolaire est purement résistif, on admet qu'il est équivalent à un conducteur ohmique c.-à-d. que la tension aux bornes du réseau et l'intensité du courant le traversant sont proportionnelles ;
Modèle:Alon détermine la résistance du conducteur ohmique équivalent au réseau dipolaire « en imposant un courant d'intensité» et « en établissant, par utilisation des lois de Kirchhoff [8], l'expression de la tension aux bornes du réseau en convention récepteur en fonction de et des résistances des composants du réseau », la résistance cherchée étant alors indépendante de [9] car le réseau est effectivement équivalent à un conducteur ohmique [10].
Étude d'un exemple : Pont résistif de Wheatstone
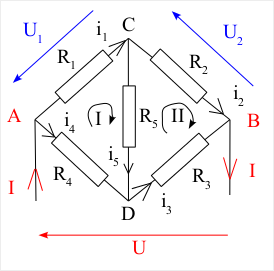
Modèle:AlOn se propose de déterminer la résistance équivalente du réseau dipolaire résistif entre les bornes et , ce réseau ne peut pas être simplifié en reconnaissant des associations en série ou en parallèle car il n'y en a pas on reconnaît une association triangle entre les nœuds , et , ces nœuds étant reliés directement par les résistances , et [12], ou une association étoile entre les nœuds , et , de nœud central , ce dernier étant relié directement aux trois autres par les résistances , et [13] voir ci-contre ;
Modèle:Alon impose donc un courant d'intensité traversant le réseau dipolaire entrant par et sortant par et on cherche à exprimer la tension entre les bornes et convention récepteur[14] en fonction de et des cinq résistances du réseau à l'exclusion de toutes autres grandeurs ;
Modèle:Alremarquant que [15] et introduisant les courants inconnus traversant les cinq branches il y a donc cinq inconnues car les tensions aux bornes des branches se déterminent en fonction de ces courants par loi d'Ohm [2] nous en déduisons ;
Modèle:Alil reste à déterminer et en fonction de et des cinq résistances du réseau par utilisation de la loi des nœuds équations indépendantes et de la loi des mailles équations indépendantes soit :
- nœud : on garde et [16], on élimine ,
- nœud : on garde et [16], on élimine ,
- nœud : on garde et [16], on élimine ,
- maille : dans laquelle on reporte et l'équation linéaire aux deux inconnues et suivante ou soit au final, en prenant l'opposé des deux membres, et
- maille : dans laquelle on reporte et l'équation linéaire aux deux inconnues et suivante ou soit finalement, en prenant l'opposé des deux membres, ;
Modèle:Alil reste à résoudre le système des deux équations linéaires aux deux inconnues et par « méthode de combinaison linéaire » [17]
Modèle:Al en remplaçant par de façon à éliminer on obtient ou, après réorganisation du dénominateur, puis
Modèle:Al en remplaçant par de façon à éliminer [18], on obtient ou, après réorganisation du dénominateur, ;
Modèle:Alon forme alors
d'où, en réécrivant sous la forme d'une fraction,
[19] dont on déduit l'expression de la résistance équivalente du réseau dipolaire résitif
Modèle:Al1er exemple : , et , on trouve «».
Modèle:Al2ème exemple : , et , on trouve «».
Utilisation de l'invariance par symétrie ou antisymétrie axiale de la répartition des courants circulant dans le réseau dipolaire résistif pour évaluer sa résistance équivalente
Préliminaire avant toute utilisation des lois de Kirchhoff pour déterminer le conducteur ohmique équivalent à un réseau dipolaire purement résistif
Modèle:AlVérifier qu'il n'y a pas d'invariance de la répartition des courants par symétrie ou antisymétrie axiale [20] sachant que l'éventuel axe de symétrie doit passer par les bornes de connexion du réseau dipolaire et que l'éventuel axe d'antisymétrie est la « médiatrice électrique » du segment limité par les bornes de connexion du réseau dipolaire.
Modèle:AlRetour sur le pont résistif de Wheatstone dans son 1er exemple : ayant
ainsi que
on en déduit que
ainsi que
c.-à-d. que l'ensemble des courants d'intensités
est invariant par symétrie axiale relativement à l'axe
et comme le courant d'intensité
est son « propre symétrique » [21], on en déduit que
Modèle:AlRetour sur le pont résistif de Wheatstone dans son 2ème exemple : ayant
ainsi que
on en déduit que
ainsi que
c.-à-d. que l'ensemble des courants d'intensités
est invariant par antisymétrie axiale par rapport à l'axe
et comme les courants d'intensité
en
et
points symétriques par rapport à
sont « antisymétriques » [23], on en déduit que
Retour sur un 1er exemple particulier de pont résistif de Wheatstone dans lequel il y a invariance par symétrie axiale de la répartition des courants

Modèle:AlLa « répartition des courants » dans le pont résistif de Wheatstone [11] ci-contre étant symétrique relativement à l'axe on en déduit que
- les points et , symétriques l'un de l'autre par rapport à l'axe de symétrie de répartition des courants , sont au même potentiel [25], il est donc possible de les court-circuiter sans modifier la répartition des courants et par suite
Modèle:Alle réseau dipolaire entre et devient une association série des deux associations parallèles d'une part et d'autre part [26]Modèle:, [27] d'où « » [28] soit, avec et , le résultat numérique suivant « » ou, - la branche étant perpendiculaire à l'axe de symétrie de répartition des courants , au point d'intersection de cette branche et de l'axe , le courant devant être d'une part perpendiculaire à l'axe et d'autre part le long de cet axe on rappelle qu'en tout point de l'axe de symétrie de répartition des courants le courant doit circuler le long de cet axe [20], est d'intensité nulle soit , on peut donc « supprimer cette branche sans modifier la répartition des courants » et par suite
Modèle:Alle réseau dipolaire entre et devient une association parallèle des deux associations série “” d'une part et “” d'autre Modèle:Nobr d'où «» ou, avec et , «» soit, avec et , le même résultat numérique «».
Retour sur un 2ème exemple particulier de pont résistif de Wheatstone dans lequel il y a invariance par antisymétrie axiale de la répartition des courants

Modèle:AlLa « répartition des courants » dans le pont résistif de Wheatstone [11] ci-contre étant antisymétrique relativement à l'axe on en déduit que
- les points et , de l'axe d'antisymétrie de répartition des courants , sont au même potentiel, demi-somme des potentiels extrêmes Modèle:Nobr il est donc possible de les court-circuiter sans modifier la répartition des courants et par suite
le réseau dipolaire entre et devient une association série des deux associations parallèles d'une part et d'autre part [26]Modèle:, [27] d'où Modèle:Nobr » ou, avec et , «» [28] soit, avec et , le résultat numérique suivant «» ou, - la branche étant le long de l'axe d'antisymétrie de répartition des courants , au point d'intersection de cette branche et de l'axe , le courant devant être d'une part le long de cet axe et d'autre part perpendiculaire à l'axe on rappelle qu'en tout point de l'axe d'antisymétrie de répartition des courants le courant doit circuler perpendiculairement à cet axe [20], est d'intensité nulle soit , on peut donc « supprimer cette branche sans modifier la répartition des courants » et par suite
le réseau dipolaire entre et devient une association parallèle des deux associations série “” et “” [27]Modèle:, [26] d'où Modèle:Nobr » ou, avec et , «» soit, avec et , le même résultat numérique «».
Autre exemple : détermination de la résistance équivalente d'un réseau métallique

Modèle:AlVoir exemple ci-contre, chaque portion de fil rectiligne étant de même longueur, de même section et de même matière donc de même résistance notée [29], on cherche à déterminer la résistance équivalente entre et dans cet exemple où, observant d'autres associations que les associations série et parallèle [7] comme des associations triangle [30] ou étoile [31], il serait nécessaire [32] d'imposer un courant d'intensité traversant le réseau et de déterminer la tension entre ses bornes par application des lois de Kirchhoff [8]Modèle:, [33] s'il n'y avait pas une invariance de la répartition des courants par symétrie ou antisymétrie axiales permettant un traitement beaucoup plus rapide.
Modèle:AlRemarques : On a indiqué le sens du courant traversant le réseau dipolaire [34] pour pouvoir préciser que la répartition des courants dans le réseau est symétrique par rapport à l'axe [35] et antisymétrique par rapport à l'axe [36] mais le résultat est indépendant de ce sens.
Modèle:AlModèle:Transparenttous les points sont des nœuds sauf les points et , on pourrait remplacer les brins et par un seul brin de résistance , de même remplacer les brins et par un seul brin de résistance , mais cela réduisant les apparentes symétrie et antisymétrie n'aurait pas été une bonne transformation.
Par utilisation de l'invariance de la répartition des courants par symétrie axiale

Modèle:AlUne 1ère façon d'utiliser l'axe de symétrie de répartition des courants est de dire que les points symétriques par rapport à sont deux à deux au même potentiel soit et par suite qu'on peut les relier deux à deux par un court-circuit sans changer la répartition des courants ;
Modèle:Alen pratique cela revient à rabattre la partie supérieure [38] du réseau sur la partie inférieure [39] de ce réseau, voir ci-contre :
- entre et passant par on a une association série de deux résistances soit [27],
- entre et passant par on a une association série de deux résistances soit [27],
- et étant montées en parallèle, entre et on a une association parallèle de deux résistances soit [37] et
- entre et on a une association série de trois résistances soit [40] et finalement
«».


Modèle:AlUne 2ème façon d'utiliser l'axe de symétrie de répartition des courants est de dire qu'en un point de l'axe de symétrie, la direction du courant doit être le long de cet axe et pour mieux appliquer cette propriété, on sépare le pointde cet axe en deux points et reliés par un court-circuit perpendiculaire à l'axe voir ci-contre à gauche ;
Modèle:Alcomme au point d'intersection de l'axe de symétrie et du court-circuit perpendiculaire à l'axe, le courant doit être simultanément le long des deux, on en déduit que l'intensité du courant à travers le court-circuit est nulle et par suite ce court-circuit n'étant traversé par aucun courant peut être supprimé sans modifier la répartition des courants voir Modèle:Nobr à droite ;
- entre et passant par on a une association série de deux résistances soit Modèle:Nobr
- entre et passant par on a une association série de deux résistances soit Modèle:Nobr
- et montées en parallèle, entre et on a une association parallèle de deux résistances soit [37],
- entre et passant par et on a une association série de trois résistances soit [40],
- entre et passant par et , comme on a la même disposition des mêmes conducteurs ohmiques que dans la partie supérieure, on en déduit [40] et
- entre et on a une association parallèle de deux résistances soit finalement
«» [37].
Par utilisation de l'invariance de la répartition des courants par antisymétrie axiale

Modèle:AlUne 1ère façon d'utiliser l'axe d'antisymétrie de répartition des courants est de dire que tous les points de l'axe d'antisymétrie sont au même potentiel moitié des potentiels extrêmes soit et par suite qu'on peut relier tous les points de l'axe d'antisymétrie par un court-circuit sans changer la répartition des courants [41] ;
Modèle:Alon obtient ainsi des associations série et parallèle de conducteurs ohmiques [42] :
- entre et on a une association parallèle de deux résistances soit [37],
- entre et passant par on a une association série d'une résistance et d'une résistance soit Modèle:Nobr
- de même entre et passant par on a la même disposition de conducteurs ohmiques qu'entre et passant par d'où ,
- et étant montées en parallèle, entre et on a une association parallèle de deux résistances soit [37],
- de même entre et on a la même disposition de conducteurs ohmiques qu'entre et d'où et
- enfin entre et on a une association série de deux résistances soit [27] et finalement


Modèle:AlUne 2ème façon d'utiliser l'axe d'antisymétrie de répartition des courants est de dire qu'en un point de l'axe d'antisymétrie, la direction du courant doit être perpendiculaire à cet axe et pour mieux appliquer cette propriété, on sépare le pointde cet axe en deux points et reliés par un court-circuit parallèle à l'axe voir ci-contre à gauche ;
Modèle:Alcomme en tout point commun de l'axe d'antisymétrie et du court-circuit parallèle à l'axe, le courant doit être simultanément perpendiculaire et parallèle à l'axe, on en déduit que l'intensité du courant à travers le court-circuit est nulle et par suite ce court-circuit n'étant traversé par aucun courant peut être supprimé sans modifier la répartition des courants Modèle:Nobr ci-contre à droite ;
Modèle:Alle schéma obtenu étant le même que le 2ème établi par utilisation de l'axe de symétrie de répartition des courants, l'évaluation se fait donc exactement de la même façon que celle faite dans le paragraphe « par utilisation de l'invariance de la répartition des courants par symétrie axiale (2ème façon) » plus haut de ce chapitre d'où le même résultat
Notion de réseau quadripolaire et conventions d'entrée et de sortie

Modèle:AlUn réseau quadripolaire R.Q. est un système électrique relié à l'extérieur par quatre bornes,
- deux bornes situées à gauche et appelées « bornes d'entrée » entre lesquelles on branche usuellement une « source » et
- deux bornes situées à droite et appelées « bornes de sortie » entre lesquelles on connecte habituellement un récepteur appelé « charge » Modèle:Nobr ci-contre :
Modèle:Alle réseau quadripolaire R.Q. est dit
- passif s'il n'y a pas de sources internes, et
- linéaire s'il n'est constitué que de dipôles linéaires au sens de l'A.R.Q.S. ;
Modèle:Alvu des bornes d'entrée le R.Q. [43] fermé sur le récepteur de sortieou chargeest un réseau dipolaire passif, on adopte la convention récepteur pour les grandeurs électriques d'entrée de ce R.D.P. [44] tension d'entrée et intensité du courant d'entrée, en conséquence la source située aux bornes de ce R.D.P. [44] est en convention générateur ;
Modèle:Alvu des bornes de sortie le R.Q. [43] fermé sur la source d'entrée est un réseau dipolaire actif, on adopte la convention générateur pour les grandeurs électriques de sortie de ce R.D.A. [45] tension de sortie et intensité du courant de sortie, en conséquence la charge située aux bornes de ce R.D.A. [45] est en convention récepteur.
Modèle:AlRemarque : on « adoptera » [46] les conventions d'écriture suivantes :
- lettres majuscules pour tension et intensité restant constantes [47] et
- lettres minuscules pour tension et intensité variant avec le temps,
- les indices pour l'entrée et la sortie étant a priori en majuscules [48].
Pont diviseur de tension, représentation de Thévenin équivalente vue de la sortie du pont diviseur de tension alimenté en entrée
Définition d'un pont diviseur de tension

Modèle:AlUn pont diviseur de tension P.D.T. est un quadripôle linéaire passif, alimenté en entrée par une tension entre les bornes de laquelle deux conducteurs ohmiques de résistances et sont montés en série quand la sortie définie aux bornes de est ouverte le pont diviseur de tension étant dit « en sortie ouverte » mais si cette sortie est fermée sur une « charge » [49], le conducteur ohmique de résistance est en série avec l'association parallèle « conducteur ohmique de résistance et charge de sortie ».
Modèle:AlLes grandeurs électriques d'entrée sont définies en convention récepteur pour l'entrée du P.D.T. [50] et simultanément en convention générateur pour la source qui l'alimente soit :
- tension d'entrée et
- intensité du courant d'entrée ;
Modèle:Alles grandeurs électriques de sortie sont définies en convention générateur pour la sortie du P.D.T. [50] et simultanément en convention récepteur pour la charge aux bornes de laquelle le P.D.T. [50] est branché soit :
- tension de sortie et
- intensité du courant de sortie [51].
Cas particulier très important du réseau dipolaire « pont diviseur de tension alimenté en entrée par uE(t) et en sortie ouverte »
Modèle:Théorème Modèle:AlDémonstration : La sortie étant ouverte ,
Modèle:AlModèle:Transparentles conducteurs ohmiques de résistance et étant montés en série sont traversés par le même courant d'intensité ,
Modèle:AlModèle:Transparentla loi d'Ohm [2] appliquée au conducteur ohmique de résistance conduit à et
Modèle:AlModèle:Transparentcelle appliquée à l'association série des conducteurs ohmiques de résistance et à d'où
Modèle:AlModèle:Transparenten éliminant par , l'expression de la tension de sortie ouverte .
Modèle:AlCommentaires : C'est de cette expression [52] que l'on tire le nom « pont diviseur de tension » en sortie ouverte car est la tension aux bornes de et montées en série et celle aux bornes de [53], tension ne représentant que la fraction de ;
Modèle:AlModèle:Transparentsi on s'intéressait à la tension aux bornes de au lieu de celle aux bornes de , on reconnaîtrait de même un pont diviseur de tension alimenté en entrée par et en sortie aux bornes de ouverte d'où [52].
Générateur de Thévenin équivalent au réseau dipolaire « pont diviseur de tension alimenté en entrée par uE(t) et vu des bornes de sortie »
Modèle:Théorème Modèle:AlDémonstration : le but recherché est la détermination de l'expression de en fonction de , et les composants résistifs du P.D.T. [50] et pour cela on utilise :
- la loi de maille [54] soit dans laquelle on élimine par
- la loi de nœud [55] ou, en explicitant en fonction de par loi d'Ohm [2] , la nouvelle expression de loi de nœud
Modèle:AlModèle:Transparentsoit, en reportant dans l'équation de maille ou ou encore soit finalement dans laquelle on reconnaît le générateur de Thévenin [56] équivalent au R.D. [57] en convention générateur à savoir
Modèle:AlCommentaires : Il est relativement facile de retrouver les caractéristiques du générateur de Thévenin [56] équivalent au R.D. [57] « P.D.T. [50] alimenté en entrée par et vu des bornes de sortie » si on les a oubliées en effet :
- d'une part la f.e.m. de Thévenin [56] étant la tension de sortie ouverte, elle représente la fraction de la tension d'entrée,
- d'autre part la résistance de Thévenin [56] étant la résistance du R.D. [57] vue des bornes de sortie quand ce dernier est rendu passif [60] c.-à-d. quand on a remplacé la tension d'entrée par un court-circuit, le R.D.P. [44] « P.D.T. court-circuité en entrée et vu des bornes de sortie » est l'association parallèle des conducteurs ohmiques de résistance et [61] soit [26].
Simplification de circuits par reconnaissance de pont(s) diviseur(s) de tension en sortie ouverte ou par utilisation du modèle de Thévenin de réseau dipolaire « pont(s) diviseur(s) de tension alimenté(s) en entrée et vu(s) des bornes de sortie »
Pont diviseur de tension alimenté en entrée par uE(t) et fermé sur une charge de résistance Ru
Modèle:AlOn souhaite déterminer la tension de sortie d'un « P.D.T. [50] alimenté en entrée par et fermé sur une charge de résistance » en fonction de , des résistances du pont et de la résistance d'utilisation ; il y a deux façons de procéder :
- Remarquer que est en sur , remplacer cette association parallèle par sa résistance équivalente et reconnaître un R.D. [57] en sortie ouverte « P.D.T. [50] alimenté en entrée par et en sortie ouverte aux bornes de »
- Remplacer le R.D. [57] « P.D.T. [50] alimenté en entrée par et vu des bornes de sortie » par son générateur de Thévenin [56] équivalent et reconnaître dans le nouveau circuit un R.D. [57] en sortie ouverte « P.D.T. [50] alimenté en entrée par , de résistance d'attaque [62] et en sortie ouverte aux bornes de »
1ère résolution : utiliser la résistance équivalente de « Ru en parallèle sur R1 »

Modèle:AlVoir schéma de situation ci-contre :
Modèle:AlOn utilise que « la résistance de la charge est montée en sur » et
Modèle:Alon remplace la résistance de l'association parallèle par sa résistance équivalente «» [26] puis,
Modèle:Alon considère le nouveau P.D.T. [50] alimenté en entrée par et en sortie ouverte aux bornes de [63] soit
ou, en multipliant haut et bas par
,
2ème résolution : utiliser le générateur de Thévenin équivalent du réseau dipolaire « pont diviseur de tension alimenté en entrée et vu des bornes de sortie »

Modèle:AlOn remplace le R.D.L. [65] « pont diviseur de tension alimenté en entrée par et vu des bornes de sortie » par le générateur de Thévenin [56] équivalent
Modèle:Alon obtient alors le schéma ci-contre à gauche :
Modèle:Alon reconnaît alors un P.D.T. [50] alimenté en entrée par
et en sortie ouverte aux bornes de
,
étant la résistance d'attaque [62] de ce nouveau P.D.T. [50] soit :
par simplification évidente
«» [66]Modèle:, [64].
Autres exemples
Modèle:AlIls sont nombreux et pourront être vus en exercices.
Modèle:AlRemarques : Avant d'appliquer le résultat du R.D. [57] « pont diviseur de tension alimenté en entrée et en sortie ouverte » vérifier que le pont diviseur de tension est effectivement en sortie ouverte ;
Modèle:AlModèle:Transparentreconnaître un pont diviseur de tension permet de résoudre beaucoup plus rapidement ce qu'on cherche, utiliser les lois de Kirchhoff [8] alors qu'un pont diviseur de tension existe doit être considéré comme une erreur tactique même si l'utilisation des lois de Kirchhoff [8] permet d'aboutir au résultat et cette dernière n'est à envisager que s'il n'y a pas de méthode plus simple [67].
Pont diviseur de courant, représentation de Norton équivalente vue de la sortie du pont diviseur de courant alimenté en entrée
Définition d'un pont diviseur de courant

Modèle:AlUn pont diviseur de courant P.D.C. est un quadripôle linéaire passif, alimenté en entrée par un courant d'intensité traversant deux conducteurs ohmiques de résistances et lesquels sont montés en parallèle quand la sortie en série avec est court-circuitée le pont diviseur de courant étant dit « en sortie court-circuitée » mais si cette sortie est fermée sur une Modèle:Nobr le conducteur ohmique de résistance est en parallèle avec l'association série « conducteur ohmique de résistance et charge de sortie ».
Modèle:AlLes grandeurs électriques d'entrée sont définies en convention récepteur pour l'entrée du P.D.C. [68] et simultanément en convention générateur pour la source qui l'alimente soit :
- intensité du courant d'entrée et
- tension d'entrée ;
Modèle:Alles grandeurs électriques de sortie sont définies en convention générateur pour la sortie du P.D.C. [68] et simultanément en convention récepteur pour la charge aux bornes de laquelle le P.D.C. [68] est branché soit :
- intensité du courant de sortie et
- tension de sortie [69].
Cas particulier très important du réseau dipolaire « pont diviseur de courant alimenté en entrée par iE(t) et en sortie court-circuitée »

Modèle:AlDémonstration : La sortie étant court-circuitée ,
Modèle:AlModèle:Transparentles conducteurs ohmiques de résistance et montés en parallèle sont soumis à la même tension ,
Modèle:AlModèle:Transparentla 2ème forme de loi d'Ohm [2] appliquée au conducteur ohmique de résistance et
Modèle:AlModèle:Transparentla même forme de loi d'Ohm [2] appliquée à l'association parallèle des conducteurs ohmiques de résistance et d'où
Modèle:AlModèle:Transparenten éliminant par , l'expression de l'intensité de courant de sortie court-circuitée ;
Modèle:AlModèle:Transparentla 2ème expression de en fonction des résistances s'obtient en remplaçant chaque conductance par l'inverse de la résistance correspondante soit .
Modèle:AlCommentaires : C'est de l'une ou l'autre expression [70] que l'on tire le nom « pont diviseur de courant » en sortie court-circuitée car est l'intensité du courant traversant et montées en parallèle et l'intensité du courant traversant [71], intensité ne représentant que la fraction de ;
Modèle:AlModèle:Transparentsi on s'intéressait à l'intensité du courant traversant au lieu de celle traversant , on reconnaîtrait de même un pont diviseur de courant alimenté en entrée par et en sortie en série avec court-circuitée d'où [70].
Générateur de Norton équivalent au réseau dipolaire « pont diviseur de courant alimenté en entrée par iE(t) et vu des bornes de sortie »
Modèle:Théorème Modèle:AlDémonstration : le but recherché est la détermination de l'expression de en fonction de , et des composants résistifs du P.D.C. [68] et pour cela on utilise :
- la loi de nœud [72] dans laquelle on élimine par
- la loi de maille [54] soit ou, en explicitant en fonction de par loi d'Ohm [2] , la nouvelle expression de loi de maille dont on tire soit
Modèle:AlModèle:Transparenten reportant dans l'équation de nœud ou ou encore soit finalement dans laquelle on reconnaît le générateur de Norton [73] équivalent au R.D. [57] en convention générateur à savoir
Modèle:AlCommentaires : Il est relativement facile de retrouver les caractéristiques du générateur de Norton [73] équivalent au R.D. [57] « P.D.C. [68] alimenté en entrée par et vu des bornes de sortie » si on les a oubliées en effet :
- d'une part le c.e.m. de Norton [73] étant l'intensité du courant de sortie court-circuitée, elle représente la fraction de l'intensité du courant d'entrée,
- d'autre part la résistance de Norton [73] étant la résistance du R.D. [57] vue des bornes de sortie quand ce dernier est rendu passif [76] c.-à-d. quand on a remplacé le courant d'entrée par un interrupteur ouvert, le R.D.P. [44] « P.D.C. [68] ouvert en entrée et vu des bornes de sortie » est alors l'association série des conducteurs ohmiques de résistance et [77] soit [27].
Simplification de circuits par reconnaissance de pont(s) diviseur(s) de courant en sortie court-circuitée ou par utilisation du modèle de Norton de réseau dipolaire « pont(s) diviseur(s) de courant alimenté(s) en entrée et vu(s) des bornes de sortie »
Pont diviseur de courant alimenté en entrée par iE(t) et fermé sur une charge de résistance Ru
Modèle:AlOn souhaite déterminer l'intensité du courant de sortie d'un « P.D.C. [68] alimenté en entrée par et fermé sur une charge de résistance » en fonction de , des résistances du pont et de la résistance d'utilisation ; il y a deux façons de procéder :
- Remarquer que est en série avec , remplacer cette association série par sa résistance équivalente et reconnaître un R.D. [57] en sortie court-circuitée « P.D.C. [68] alimenté en entrée par et en sortie court-circuitée en série avec »
- Remplacer le R.D. [57] « P.D.C. [68] alimenté en entrée par et vu des bornes de sortie » par son générateur de Norton [73] équivalent et reconnaître dans le nouveau circuit un R.D. [57] en sortie court-circuitée « P.D.C. [68] alimenté en entrée par , de résistance d'attaque [78] et en sortie court-circuitée en série avec »
1ère résolution : utiliser la résistance équivalente de « Ru en série avec R1 »

Modèle:AlVoir schéma de situation ci-contre :
Modèle:AlOn utilise que « la résistance de la charge est montée en série avec » et
Modèle:Alon remplace la résistance de l'association série par sa résistance équivalente «» [27] puis,
Modèle:Alon considère le nouveau P.D.C. [68] alimenté en entrée par et en sortie court-circuitée en série avec [63] soit
que l'on peut réécrire selon
2ème résolution : utiliser le générateur de Norton équivalent du réseau dipolaire « pont diviseur de courant alimenté en entrée et vu des bornes de sortie »

Modèle:AlOn remplace le R.D.L. [65] « pont diviseur de courant alimenté en entrée par et vu des bornes de sortie » par le générateur de Norton [73] équivalent
Modèle:Alon obtient alors le schéma ci-contre à gauche :
Modèle:Alon reconnaît alors un P.D.C. [68] alimenté en entrée par
et en sortie court-circuitée en série avec
,
étant la résistance d'attaque [78] de ce nouveau P.D.C. [68] soit :
par simplification évidente
«» [80]Modèle:, [79].
Autres exemples
Modèle:AlIls sont beaucoup moins nombreux que ceux utilisant les P.D.T. [50] et pourront être vus en exercices.
Modèle:AlRemarques : Avant d'appliquer le résultat du R.D. [57] « pont diviseur de courant alimenté en entrée et en sortie court-circuitée »
Modèle:AlModèle:Transparentvérifier que le pont diviseur de courant est effectivement en sortie court-circuitée ;
Modèle:AlModèle:Transparentreconnaître un pont diviseur de courant permet de résoudre plus rapidement ce qu'on cherche, utiliser les lois de Kirchhoff [8] alors qu'un pont diviseur de courant existe doit être considéré comme maladroit et cette utilisation n'est à envisager que s'il n'y a pas de méthode plus simple [81].
Association parallèle de deux sources linéaires non idéales de tension, représentation de Thévenin équivalente à l'association, théorème de Millman appliqué au cas de deux branches du type « R, V » délivrant un courant d'intensité connue (ou à connaître)
Association parallèle de deux sources linéaires non idéales de tension et générateur de Thévenin équivalent à l'association

Modèle:AlConsidérons le montage ci-contre dans lequel on a représenté les sources linéaires non idéales de tension par leur modèle générateur de Thévenin [56] ; vu des bornes de sortie ce R.D. [57] « association parallèle de sources non idéales de tension » est équivalente à un générateur de Thévenin [56] dont nous cherchons la f.e.m. de Thévenin[56] et la résistance de Thévenin[56] :
Modèle:Alle plus simple pour l'obtenir est de transformer chaque source réelle de tension en son modèle générateur de Norton [73]Modèle:, [82] à savoir une « association parallèle d'une source de courant parfaite de c.e.m. et d'un conducteur ohmique de résistance Modèle:Nobr puis de remplacer
- les deux conducteurs ohmiques en parallèle par leur conducteur ohmique équivalent de résistance [26] ainsi que
- les deux sources de courant parfaites en parallèle par leur source de courant parfaite équivalente de c.e.m. « » [83] ;
Modèle:Alon obtient alors le modèle générateur de Norton [73] du R.D. [57] « association parallèle de sources non idéales de tension » c.-à-d. l'association d'une source de courant parfaite de c.e.m. et d'un conducteur ohmique de résistance [82] et
Modèle:Alil reste transformer ce générateur de Norton [73] en un générateur de Thévenin [56] équivalent pour établir le générateur de Thévenin [56] équivalent au R.D. [57] initial « association parallèle de sources non idéales de tension » c.-à-d. l'association série d'une source de tension parfaite de f.e.m. « » et d'un conducteur ohmique de résistance «» [82].
Modèle:AlConclusion : le générateur de Thévenin [56] équivalent au R.D. [57] « association parallèle de sources non idéales de tension » a pour
- f.e.m. de Thévenin[56] «» C.L. [84] des f.e.m. des sources, les cœfficients des f.e.m. étant croisés « pour et pour » et
- résistance de Thévenin[56] «» résistance équivalente entre et du R.D. [57] rendu passif en remplaçant les sources idéales de tension par des courts-circuits ;
Modèle:AlModèle:Transparentla loi d'Ohm [2] généralisée du générateur de Thévenin [56] équivalent au R.D. [57] « association parallèle de sources non idéales de tension » s'écrit donc, en convention générateur :
Modèle:AlCommentaires : Le R.D. [57] « pont diviseur de tension alimenté en entrée par avec sortie aux bornes du conducteur ohmique de résistance » est un cas particulier de ce R.D. [57] « association parallèle de sources non idéales de tension » avec , le générateur de Thévenin [56] équivalent a donc la même résistancede Thévenin[56] «» [85] et sa f.e.m. qui, dans le Modèle:Nobr « association parallèle de sources non idéales de tension » était une C.L. des f.e.m. des sources, les cœfficients des f.e.m. étant croisés « pour et pour » devient, en imposant, « » [86].
Complément : théorème de Millman appliqué au nœud d'où partent deux branches de type « R, V » lesquelles délivrent un courant d'intensité « iS » connue (ou à connaître)
permet le plus souvent un traitement plus rapide.

Modèle:AlIl s'agit du résultat du paragraphe précédent réécrit en termes de potentiel du nœud où on applique le théorème de Millman [87] voir schéma ci-contre :
Modèle:Alon pourra appliquer le théorème de Millman [87] en un nœud si, arrivent à ce nœud deux branches internes du type [90]Modèle:, [89], la branche externe permettant le départ d'un courant d'intensité ;
Modèle:Alle théorème de Millman [87] appliqué au nœud permet de déterminer le potentiel du nœud considéré en fonction des deux potentiels et des deux résistances définis sur chaque branche interne ainsi que de l'intensité du courant délivré [91] ;
Modèle:All'« association parallèle de deux sources non idéales de tension » délivrant un courant d'intensité satisfait aux conditions d'« utilisation du théorème de Millman au nœud » si « on choisit la masse en » voir schéma du paragraphe précédent[92] ;
Modèle:Alor ayant établi «
» [93] on peut réécrire cette relation en termes de potentiels car «
» [94] soit «
» ou, en divisant haut et bas par
[95], l'expression suivante
Modèle:Théorème
Modèle:AlCommentaires : Pour appliquer le théorème de Millman [87] en un nœud, vérifier que les deux branches internes sont de type choisir la « masse » [96] pour que les potentiels soient les plus simples possibles et définir le courant délivré dans la branche externe ;
Modèle:AlModèle:Transparentle potentiel du nœud choisi est exprimé sous la forme d'un quotient d'une somme de trois intensités sur une somme de deux conductances, chaque branche interne ayant pour terme dans la somme du numérateur et pour terme dans la somme du dénominateur , la branche externe n'ayant que le terme [97] dans la somme du numérateur.
Compléments : généralisation du théorème de Millman
il est toutefois très pratique et son utilisation dans des circuits compliqués est quasi indispensable pour un traitement de durée acceptable.
Condition d'application du théorème de Millman en un nœud duquel part une branche externe par laquelle le courant est délivré

Modèle:AlIl s'agit de la généralisation du théorème de Millman [87] avec modification des branches internes voir schéma Modèle:Nobr
Modèle:Alon pourra appliquer la généralisation du théorème de Millman [87] en un nœud si, arrivent à ce nœud des branches internes du type [90] et (ou) des branches internes de type [98]Modèle:, [89]Modèle:, [99], la branche externe permettant le départ d'un courant d'intensité ;
Modèle:Alla généralisation du théorème de Millman [87] appliquée au nœud permet de déterminer le potentiel du nœud considéré en fonction des potentiels et des résistances définis sur chaque branche interne de type ainsi que des intensités des courants traversant chaque branche interne de type et l'intensité du courant délivré [91].
Énoncé du théorème de Millman appliqué au nœud S du réseau par lequel le courant d'intensité iS en sort
Modèle:AlLa démonstration consiste
- à transformer les branches de type en leur modèle générateur de courant [100],
- à considérer les courants des branches de type comme des courants délivrés par des sources idéales de courant,
- à regrouper les c.e.m. en parallèle en un seul c.e.m. équivalent
- puis regrouper les conducteurs ohmiques en parallèle résultant des modèles générateurs de courant équivalents aux branches de type en un seul conducteur ohmique équivalent de conductance
- pour terminer en écrivant que ce conducteur ohmique équivalent est traversée par le courant d'intensité [97] d'où «».
Intérêt du théorème de Millman
Modèle:AlSi on cherche à déterminer le générateur de Thévenin [56] équivalent à un R.D.A. [45] comportant une ou plusieurs sources, il peut être intéressant dans le cas où la notion de pont diviseur de tension « ne serait pas opérationnelle » [101] d'appliquer le théorème de Millman [87] en « chaque borne extrême et du réseau » [102] pour déterminer le potentiel de chaque borne en fonction des grandeurs internes et de l'« intensité du courant traversant le réseau » [103], puis de faire la différence pour obtenir la tension aux bornes du réseau ;
Modèle:Alayant obtenu [104] par application du théorème de Millman [87] en et
Modèle:AlModèle:Transparent[105] par application du théorème de Millman [87] en ,
Modèle:Alla différence s'écrit alors «» et on reconnaît la loi d'Ohm [2] généralisée,
Modèle:AlNous pourrons voir des exemples en exercices en plus de celui traité dans le paragraphe suivant [108].
Exemple d'utilisation du théorème de Millman : pont résistif de Wheatstone

Modèle:AlSoit le pont résistif de Wheatstone représenté ci-contre, alimenté en entrée par une source de tension parfaite de f.e.m. constante et délivrant, à travers un ampèremètre de résistance interne branché entre les bornes de sortie, un courant d'intensité [109] ;
Modèle:Alsouhaitant évaluer l'intensité en fonction de , des quatre résistances du pont et de , on détermine au préalable le générateur de Thévenin [56] équivalent au R.D. [57] « pont de Wheatstone [11] alimenté en entrée par et vu des bornes de sortie » par utilisation du théorème de Millman [87] successivement à chacune des bornes de sortie ;
Modèle:Alon choisit la masse en ce qui permet de connaître en plus de ;
Modèle:Alapplication du théorème de Millman au nœud : il s'agit du théorème à deux branches internes de type avec une branche externe par laquelle un courant d'intensité s'éloigne de soit « » ou, en multipliant par haut et bas, « » [110] ;
Modèle:Alapplication du théorème de Millman au nœud : il s'agit du théorème à deux branches internes de type avec une branche externe par laquelle un courant d'intensité s'approche de soit « » ou, en multipliant haut et bas par , on obtient «» [111] ;
Modèle:Alon termine en faisant la différence pour obtenir la tension aux bornes du R.D. [57] « pont de Wheatstone alimenté en entrée par
et vu des bornes de sortie » soit
Modèle:Alet on en tire le générateur de Thévenin [56] équivalent

Modèle:Alnous obtenons finalement le schéma de sortie équivalent représenté ci-contre :
Modèle:Alon en déduit l'intensité du courant traversant l'ampèremètre par loi de Pouillet [113]Modèle:, [114] soit
;
Modèle:Alle sens du courant dépendant du signe de
, on observe l'absence de courant dans l'ampèremètre quand la f.e.m. de Thévenin [56] du générateur de Thévenin [56] équivalent au R.D. [57] « pont de Wheatstone [11] alimenté en entrée par
et vu des bornes de sortie » est nulle soit
Notes et références
- ↑ On rappelle qu'une source réelle de tension est une association série d'une source idéale de tension et d'un conducteur ohmique et
Modèle:AlModèle:Transparentune source réelle de courant est une association parallèle d'une source idéale de courant et d'un conducteur ohmique. - ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 2,10 et 2,11 Georg Simon Ohm (1789 - 1854) physicien allemand essentiellement connu pour sa découverte de la loi qui porte maintenant son nom.
- ↑ 3,0 et 3,1 Erreur de référence : Balise
<ref>incorrecte : aucun texte n’a été fourni pour les références nomméesÀ retenir - ↑ La méthode par itération n'est acceptable que s'il n'y a pas plus de trois conducteurs ohmiques montés en parallèle, sinon préférer le calcul de la conductance équivalente et l'inversion pour en déduire la résistance équivalente.
- ↑ Toutes les inhomogénéités criantes comme celles-ci doivent être repérées IMPÉRATIVEMENT.
- ↑ Rappels pour ceux qui ont tendance confondre les associations en série et parallèle :
- deux conducteurs ohmiques sont montés en série entre deux bornes si, de la 3ème borne celle située entre les deux conducteurs ohmiques il n'y a aucun autre fil de connexion que ceux qui partent vers les conducteurs ohmiques autrement dit si cette borne n'est pas un nœud et
- deux conducteurs ohmiques sont montés en parallèle entre deux bornes si chacune de celles-ci est reliée directement par des fils de connexion à l'un et l'autre des conducteurs ohmiques.
- ↑ 7,0 et 7,1 Ces autres associations seront détaillées ultérieurement, mais elles peuvent se regrouper en deux types :
Modèle:Alles associations de conducteurs ohmiques en triangle entre trois nœuds chacun de ces nœuds est directement relié aux deux autres par un conducteur ohmique,
Modèle:Alles associations de conducteurs ohmiques en étoile entre trois nœuds chacun de ces nœuds est directement relié à un 4ème nœud central par un conducteur ohmique. - ↑ 8,0 8,1 8,2 8,3 et 8,4 Gustav Robert Kirchhoff (1824 – 1887) est l'un des plus grands physiciens d'origine allemande prussienne du XIXème siècle ; bien qu'il doive sa célébrité aux lois relatives au courant électrique dans les circuits, lois qu'il a établies alors qu'il était encore étudiant, c'est surtout en tant que fondateur, avec Robert Whilhelm Bunsen (1811 - 1899) chimiste allemand, de la spectroscopie qu'il a apporté sa plus grande contribution à la science.
- ↑ Cela résulte du fait que la tension aux bornes du réseau dipolaire est à l'intensité du courant le traversant, les lois de maille et les lois de nœud étant linéaires et le réseau ne contenant pas de sources la seule source créant le courant d'intensité étant extérieure au réseau.
- ↑ Ne jamais perdre de vue entre quelles bornes on cherche l'équivalence du réseau et pour cela, ceux qui auraient des soucis peuvent faire ressortir ces bornes en une couleur différente des autres bornes.
- ↑ 11,0 11,1 11,2 11,3 11,4 11,5 11,6 et 11,7 Charles Wheatstone (1802 - 1875) physicien et inventeur anglais à qui on doit, entre autres, la 1ère liaison télégraphique filaire longue de près de Londres en , l'un des premiers microphones et bien sûr le pont résistif du même nom.
- ↑ On peut remplacer cette association triangle par une autre entre les nœuds , et , ces nœuds étant reliés directement par les résistances , et .
- ↑ On peut remplacer cette association étoile par une autre entre les nœuds , et , de nœud central , ce dernier étant relié directement aux trois autres par les résistances , et .
- ↑ Le sens du courant pouvant bien sûr être inversé, à condition d'inverser aussi le sens de tension pour rester en convention récepteur.
- ↑ On aurait pu écrire aussi , on aurait évidemment trouvé le même résultat au final.
- ↑ 16,0 16,1 et 16,2 On va résoudre le système de cinq équations linéaires aux cinq inconnues par la méthode de substitution voir le paragraphe « résolution par substitution (d'un système de n équations algébriques linéaires à n inconnues) » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ Voir le paragraphe « résolution par combinaison (linéaire) » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ Ceci est plus rapide pour obtenir le résultat littéral de ; si nous n'avions à déterminer que sa valeur numérique l'utilisation de l'équation aurait été la méthode la plus rapide.
- ↑ La proportionnalité de la tension aux bornes du réseau à l'intensité du courant le traversant justifie que le réseau est équivalent à un conducteur ohmique.
- ↑ 20,0 20,1 et 20,2 Voir la définition de l'« invariance par symétrie axiale d'un champ vectoriel d'un espace à deux dimensions plan » et de l'« invariance par antisymétrie axiale d'un champ vectoriel d'un espace à deux dimensions plan » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ En et il est effectivement porté par dans la pratique les fils de connexion ne sont pas coudés en et mais dans le prolongement du réseau dipolaire.
- ↑ En effet l'invariance par symétrie axiale de tous les courants à l'exception de celui d'intensité a été vérifiée, si ceci n'était pas vrai pour cela devrait ne pas l'être au moins pour un autre courant par utilisation de la loi des nœuds.
- ↑ En et ils sont effectivement perpendiculaires à et ils ont évidemment même intensité.
- ↑ En effet l'invariance par antisymétrie axiale de tous les courants à l'exception de celui d'intensité a été vérifiée, si ceci n'était pas vrai pour cela devrait ne pas l'être au moins pour un autre courant par utilisation de la loi des nœuds.
- ↑ En effet entre et d'une part et et d'autre part, les résistances sont les mêmes et les intensités du courant aussi d'où une même tension ou une même d.d.p. .
- ↑ 26,0 26,1 26,2 26,3 26,4 et 26,5 Voir le paragraphe « association parallèle de deux conducteurs ohmiques, résistance équivalente » plus haut dans ce chapitre.
- ↑ 27,0 27,1 27,2 27,3 27,4 27,5 27,6 et 27,7 Voir le paragraphe « association série de deux conducteurs ohmiques » plus haut dans ce chapitre.
- ↑ 28,0 et 28,1 La résistance équivalente ne dépend pas de car le conducteur ohmique branché entre et points au même potentiel n'est traversé par aucun courant comme on court-circuite les points et , la résistance équivalente de l'association “ en parallèle sur le court-circuit ” est nulle.
- ↑ On établit que la résistance d'un fil rectiligne est proportionnelle à sa longueur, à la résistivité de la matière qui le compose et inversement proportionnelle à l'aire de sa section droite.
- ↑ Exemples de triangle : on rappelle que n'est pas un nœud et on rappelle que n'est pas un nœud.
- ↑ Exemples d'étoile : entre les nœuds de nœud central ou entre les nœuds de nœud central on rappelle que n'est pas un nœud, entre les nœuds de nœud central ou entre les nœuds de nœud central on rappelle que n'est pas un nœud, entre les nœuds de nœud central ou encore entre les nœuds de nœud central .
- ↑ Il suffit qu'il y ait une seule association triangle ou étoile pour que cela soit nécessaire.
- ↑ Ce qui serait compliqué car le réseau dipolaire ayant nœuds avec les deux bornes d'entrée et de sortie et branches, cela nécessiterait la résolution d'un système linéaire de équations aux inconnues obtenues à l'aide de équations de nœuds et équations de mailles indépendantes.
- ↑ On a aussi indiqué la tension aux bornes du réseau dipolaire correspondant à la convention récepteur mais on ne s'en servira pas.
- ↑ En effet au-dessus et au-dessous de l'axe on observe la même répartition des résistances d'une part et d'autre part le courant d'intensité arrivant en selon la direction de l'axe, ressort par selon la même direction, en accord avec la direction que doit avoir le courant en des points d'un axe de symétrie.
- ↑ En effet à gauche et à droite de l'axe on observe la même répartition des résistances d'une part et d'autre part le courant d'intensité arrivant en selon une direction et un sens précis, ressort par , symétrique de par rapport à l'axe , selon une direction et un sens antisymétrique, en accord avec la direction et le sens que doivent avoir le courant en des points symétriques par rapport à un axe d'antisymétrie.
- ↑ 37,0 37,1 37,2 37,3 37,4 et 37,5 On rappelle que l'association parallèle de deux conducteurs ohmiques de même résistance est équivalente à un conducteur ohmique dont la résistance est la moitié des résistances des composants de l'association voir le paragraphe « association parallèle de deux conducteurs ohmiques, résistance équivalente (cas particulier) » plus haut dans ce chapitre.
- ↑ C.-à-d. située au-dessus de l'axe de symétrie.
- ↑ C.-à-d. située au-dessous de l'axe de symétrie.
- ↑ 40,0 40,1 et 40,2 Voir le paragraphe « généralisation : association série de plus de deux conducteurs ohmiques » plus haut dans ce chapitre.
- ↑ En général ce n'est pas la meilleure façon de résoudre le problème car les points de l'axe d'antisymétrie sont, par définition, uniquement localisés au niveau de l'axe d'antisymétrie
- ↑ Mais du fait que la modification ne concerne que des points localisés au niveau de l'axe d'antisymétrie, il est le plus souvent nécessaire mais pas ici d'utiliser également une invariance par symétrie du réseau transformé quand celle-ci existe bien entendu.
- ↑ 43,0 et 43,1 Réseau Quadripolaire.
- ↑ 44,0 44,1 44,2 et 44,3 Réseau Dipolaire Passif.
- ↑ 45,0 45,1 et 45,2 Réseau Dipolaire Actif.
- ↑ Usage courant mais ne correspondant pas à une règle obligatoire, néanmoins utilisée par la quasi unanimité des usagers.
- ↑ Pour l'instant cela correspond uniquement au régime permanent, mais en régime sinusoïdal, l'amplitude étant une constante sera aussi notée en majuscule.
- ↑ Les indices pour les grandeurs variant avec le temps seront en minuscules dans le cas d'un régime sinusoïdal à valeur moyenne nulle, sinon donc dans le cas le plus général les indices resteront en majuscules.
- ↑ Ce qui est le cas le plus général même si ce n'est pas le plus utilisé.
- ↑ 50,00 50,01 50,02 50,03 50,04 50,05 50,06 50,07 50,08 50,09 50,10 50,11 50,12 50,13 50,14 50,15 et 50,16 Pont Diviseur de Tension.
- ↑ Celle-ci étant nulle quand le P.D.T. est en sortie ouverte.
- ↑ 52,0 et 52,1 Il faut bien sûr vérifier que les tensions d'entrée et de sortie sont dans le même sens.
- ↑ Le plus souvent notée .
- ↑ 54,0 et 54,1 Dans le sens indiqué sur le schéma.
- ↑ Loi de nœud à la borne supérieure de sortie.
- ↑ 56,00 56,01 56,02 56,03 56,04 56,05 56,06 56,07 56,08 56,09 56,10 56,11 56,12 56,13 56,14 56,15 56,16 56,17 56,18 56,19 56,20 56,21 56,22 56,23 56,24 56,25 56,26 56,27 56,28 56,29 56,30 56,31 56,32 et 56,33 Erreur de référence : Balise
<ref>incorrecte : aucun texte n’a été fourni pour les références nomméesThévenin - ↑ 57,00 57,01 57,02 57,03 57,04 57,05 57,06 57,07 57,08 57,09 57,10 57,11 57,12 57,13 57,14 57,15 57,16 57,17 57,18 57,19 57,20 57,21 57,22 57,23 57,24 et 57,25 Réseau Dipolaire.
- ↑ Valeur de tension de sortie à vide c.-à-d. quand .
- ↑ Quand le R.D. est rendu passif en annulant la f.e.m. de Thévenin on obtient en convention générateur d'où .
- ↑ C.-à-d. quand on a annulé la f.e.m. de Thévenin ce qui s'obtient en annulant la tension d'entrée en effet la f.e.m. de Thévenin est à la tension d'entrée.
- ↑ En effet, entre les bornes de sortie, est montée en parallèle sur l'autre branche « court-circuit en série avec ».
- ↑ 62,0 et 62,1 C.-à-d la résistance aux bornes de laquelle n'est pas définie la sortie.
- ↑ 63,0 et 63,1 Schéma équivalent qu'il conviendrait de tracer.
- ↑ 64,0 et 64,1 On vérifie que si , .
- ↑ 65,0 et 65,1 Réseau Dipolaire Linéaire.
- ↑ Correspondant effectivement au même résultat que celui obtenu au paragraphe précédent car .
- ↑ Attention les P.D.T. ne se trouvent pas dans tous les réseaux, mais il y a pratiquement toujours d'autres méthodes non encore étudiées plus rapides que l'utilisation des lois de Kirchhoff.
- ↑ 68,00 68,01 68,02 68,03 68,04 68,05 68,06 68,07 68,08 68,09 68,10 68,11 68,12 68,13 68,14 68,15 et 68,16 Pont Diviseur de Courant.
- ↑ Celle-ci étant nulle quand le P.D.C. est en sortie court-circuitée.
- ↑ 70,0 et 70,1 Il faut bien sûr vérifier que les courants d'entrée et de sortie ont un sens adapté l'un à l'autre.
- ↑ Le plus souvent notée .
- ↑ Loi de nœud à la borne supérieure d'entrée.
- ↑ 73,00 73,01 73,02 73,03 73,04 73,05 73,06 73,07 73,08 73,09 73,10 73,11 73,12 et 73,13 Erreur de référence : Balise
<ref>incorrecte : aucun texte n’a été fourni pour les références nomméesNorton - ↑ Valeur d'intensité de courant de sortie court-circuitée c.-à-d. quand .
- ↑ Quand le R.D. est rendu passif en annulant le c.e.m. de Norton on obtient en convention générateur d'où .
- ↑ C.-à-d. quand on a annulé le c.e.m. de Norton ce qui s'obtient en annulant l'intensité du courant d'entrée en effet le c.e.m. de Norton est à l'intensité du courant d'entrée.
- ↑ En effet, entre les bornes de sortie, est montée en série avec l'autre association « interrupteur ouvert en parallèle sur ».
- ↑ 78,0 et 78,1 C.-à-d. la résistance autre que celle en série de laquelle est définie la sortie.
- ↑ 79,0 et 79,1 On vérifie que si , .
- ↑ Correspondant effectivement au même résultat que celui obtenu au paragraphe précédent.
- ↑ Attention les P.D.C. ne se trouvent pas dans tous les réseaux, mais il y a pratiquement toujours d'autres méthodes non encore étudiées plus rapides que l'utilisation des lois de Kirchhoff.
- ↑ 82,0 82,1 82,2 et 82,3 Schéma équivalent à tracer effectivement soi-même.
- ↑ L'association parallèle de deux sources de courant parfaites est effectivement une source de courant parfaite dont le c.e.m. est la somme des c.e.m. de chaque source car ainsi que entraînent, avec application de la loi des nœuds, la relation suivante caractérisant une source de courant parfaite de c.e.m. .
- ↑ Combinaison Linéaire.
- ↑ Résistance équivalente du R.D. « association parallèle de sources non idéales de tension » que l'on a rendu passif en imposant et .
- ↑ On retrouve donc bien la f.e.m. du générateur de Thévenin équivalent au « pont diviseur de tension alimenté en entrée par avec sortie aux bornes du conducteur ohmique de résistance » identifiable à la tension à vide .
- ↑ 87,00 87,01 87,02 87,03 87,04 87,05 87,06 87,07 87,08 87,09 87,10 87,11 87,12 87,13 et 87,14 Jacob Millman (1911 - 1991) électronicien américain né en Russie à Novohrad-Volynskyï de nos jours en Ukraine, devenu américain par suite de l'émigration de ses parents, on lui doit essentiellement le théorème portant son nom.
- ↑ 88,0 et 88,1 En effet il n'est pas explicitement précisé dans le programme de physique de PCSI.
- ↑ 89,0 89,1 89,2 89,3 et 89,4 Usuellement les lettres majuscules sont réservées pour des grandeurs indépendantes du temps, ici exceptionnellement on utilise et pour des grandeurs dépendant de pour accroître les possibilités d'écriture mais on réservera cet emploi lors de l'utilisation du théorème de Millman.
- ↑ 90,0 et 90,1 C.-à-d. que l'on trouve, sur chaque branche, un conducteur ohmique de résistance connue, à l'extrémité duquel le potentiel , évalué relativement à un point interne appelé « masse », est connu.
- ↑ 91,0 et 91,1 Il faut auparavant choisir la masse du circuit pour avoir le traitement le plus simple même si cette masse peut, a priori, être n'importe quel point interne.
- ↑ En effet la traversée du conducteur ohmique de résistance conduit au potentiel connu et celle du conducteur ohmique de résistance au potentiel connu dans un réseau satisfaisant l'applicabilité du théorème de Millman, les différences de potentiel entre les potentiels connus et la masse ne sont pas nécessairement des tensions aux bornes de source idéale de tension, elles sont simplement fixées à l'instant et sont équivalentes à ce qu'on obtiendrait aux bornes d'une source idéale de tension.
- ↑ Voir le paragraphe « association parallèle de deux sources linéaires non idéales de tension et générateur de Thévenin équivalent à l'association (conclusion) » plus haut dans ce chapitre.
- ↑ On rappelle que la masse a été choisie en .
- ↑ Le but étant d'obtenir une expression plus symétrique, et donc plus facile à appliquer.
- ↑ Si le circuit étudié est un R.D., le nœud d'application du théorème de Millman étant l'une des bornes, l'autre borne ne sera pas systématiquement choisi comme masse voir exercices.
- ↑ 97,0 et 97,1 À transformer en si le courant est reçu au lieu d'être délivré.
- ↑ C.-à-d. une branche interne traversée par un courant d'intensité connue.
- ↑ Avec l'exigence supplémentaire qu'il doit y avoir au moins une branche de type .
- ↑ C.-à-d. une source idéale de courant de c.e.m. en parallèle sur un conducteur ohmique de résistance .
- ↑ Cela est rare dans les R.D. simples mais devient plus fréquent quand la complication des R.D. s'accroît.
- ↑ Attention si le réseau délivre par la borne un courant d'intensité , il reçoit par la borne ce courant d'intensité c._à-d. que le réseau délivre par la borne un courant d'intensité .
- ↑ Si le courant d'intensité sort par la borne , dans le numérateur contiendra , il rentre alors par la borne et dans le numérateur contiendra .
- ↑ En supposant que le courant d'intensité sort par la borne , le terme indépendant de est le potentiel à vide valeur du potentiel si et le cœfficient de est négatif noté .
- ↑ En supposant que le courant d'intensité sort par la borne , il entre par la borne , le terme indépendant de est le potentiel à vide valeur du potentiel si et le cœfficient de est positif noté .
- ↑ Tension à vide du R.D. c.-à-d. quand .
- ↑ Valeur de la résistance équivalente du R.D. quand ce dernier a été rendu passif c.-à-d. en imposant .
- ↑ Dans la mesure où il n'y a qu'une seule source, ce dernier pourrait être traité uniquement à l'aide de ponts diviseurs de tension.
- ↑ Bien que l'intensité du courant soit constante il n'est pas interdit de l'écrire en minuscule.
- ↑ Ce résultat pouvait être trouvé en considérant le R.D. « P.D.T. alimenté en entrée c.-à-d. entre et par et délivrant en sortie par un courant d'intensité » dont le générateur de Thévenin équivalent a
- pour f.e.m. de Thévenin quand la tension aux bornes de est la fraction de celle aux bornes de et
- pour résistance de Thévenin quand c.-à-d. quand et sont reliés par un court-circuit, les conducteurs de résistance et sont en vu des points et .
- ↑ Ce résultat pouvait être trouvé en considérant le R.D. « P.D.T. alimenté en entrée c.-à-d. entre et par et délivrant en sortie par un courant d'intensité » dont le générateur de Thévenin équivalent a
- pour f.e.m. de Thévenin quand la tension aux bornes de est la fraction de celle aux bornes de et
- pour résistance de Thévenin quand c.-à-d. quand et sont reliés par un court-circuit, les conducteurs de résistance et sont en vu des points et .
- ↑ Réseau Dipolaire Linéaire Actif.
- ↑ Claude Servais Mathias Pouillet (1790 - 1868) physicien et homme politique français, on lui doit essentiellement des travaux portant sur la compressibilité des gaz et sur les lois expérimentales relatives à l'intensité du courant électrique dans un circuit fermé il sut préciser la notion de résistance électrique, montrer que les générateurs sont composés d'une force électromotrice pure et d'une résistance intérieure et il établit la loi qui porte son nom.
- ↑ La loi de Pouillet s'applique pour déterminer l'intensité du courant circulant dans un circuit série en régime permanent, elle résulte de l'application de la loi des mailles avec choix du sens de f.e.m. dans le sens du courant en accord avec l'algébrisation habituelle et s'énonce «» à retenir et à savoir utiliser sans hésitation.
- ↑ Le pont est équilibré quand les deux produits des résistances croisées sont égaux ; si on utilise trois résistances étalon c.-à-d. connues avec une bonne précision variables on peut déterminer la valeur de la 4ème résistance inconnue en cherchant à équilibrer le pont de Wheatstone.