Probabilités conditionnelles/Introduction

Modèle:Chapitre Ce premier chapitre pose les fondements des probabilités conditionnelles.

Approche et définition

Si l'on étudie, sur une population donnée, la probabilité de réalisation d'un certain événement, on peut parfois être amené à se limiter à une certaine partie de la population. Il est possible alors que la probabilité de réalisation de cet événement ne soit pas la même sur la population totale et sur la restriction de la population que l'on a choisie.

On peut aussi considérer qu'un événement A influe par sa présence sur la réalisation d'un événement B.

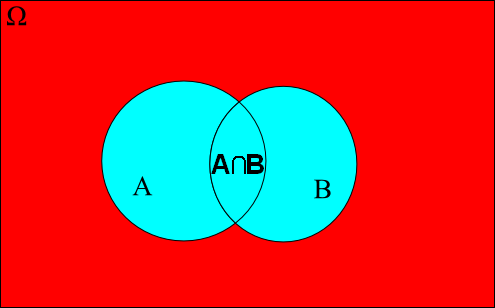
Les deux exemples précédents nous montrent que si l'on considère deux événements A et B qui ne sont pas indépendants l'un de l'autre, c'est-à-dire si la réalisation de l'un influe sur la réalisation de l'autre, nous pouvons être amenés à définir plusieurs probabilités pour décrire le degré d'influence de l'un des événements sur l'autre. Supposons, pour fixer les idées, que la réalisation de l'événement A affecte la probabilité de réalisation de l'événement B. Même si nous connaissons la probabilité de réalisation de l'événement B sans tenir compte de la réalisation de l'événement A, nous ne pourrons pas utiliser celle-ci si nous savons que l'événement A est réalisé. Nous définirons une nouvelle probabilité de réalisation de l'événement B en présence de l'événement A.

Calcul d'une probabilité conditionnelle

Dans ce paragraphe, nous allons donner une formule de calcul d'une probabilité conditionnelle.

Nous nous placerons d'abord dans le cas simplifié d'un univers $\mathrm{\Omega }$ où tous les événements élémentaires sont équiprobables. Nous savons qu'alors, la probabilité d'un événement $M$ peut se calculer pas la formule :

Soit maintenant deux événements $A$ et $B$ de $\mathrm{\Omega }$ :

Voyons comment utiliser la formule précédente pour calculer la probabilité $P_A(B)$. Si l'on sait que l'événement A est réalisé, alors tous les cas possibles seront les événements élémentaires de $\mathrm{\Omega }$ qui seront dans $A$. Les cas favorables seront alors tous les événements élémentaires qui réalisent $B$ tout en restant dans $A$. Autrement dit, ce seront les événements qui se trouveront dans $A\cap B$. Nous aurons alors :

$P_A(B)=\frac{\text{cas favorables}}{\text{cas possibles}}=\frac{p(A\cap B)}{p(A)}$.

En se limitant aux univers formés d'événements équiprobables, nous avons obtenu la formule :

$P_A(B)=\frac{p(A\cap B)}{p(A)}$.

Nous admettrons que cette formule reste valable pour des univers quelconques.

Nous retiendrons :

Modèle:Exemple

Autres formules

$p_A(B)$ représente la probabilité de l'événement $B$ sachant que $A$ est réalisé. Mais si $A$ est réalisé, on peut éventuellement voir $A$ comme un événement certain. En fait, tout se passe comme si l'on changeait d'univers. L'événement $A$ peut être vu comme un nouvel univers qui vient remplacer $\mathrm{\Omega }$. La probabilité $p_A(B)$ pourrait alors être définie comme la probabilité de l'événement $B$ en prenant $A$ comme nouvel univers.

Si nous avons dit cela, c'est pour dire que toutes les formules qui étaient valables dans l'univers $\mathrm{\Omega }$ sont aussi valables dans le pseudo nouvel univers $A$.

On aura, par exemple : Modèle:Encadre

On pourrait aussi écrire avec trois événements $A$, $B$ et $C$ quelconques : Modèle:Encadre(mais cette formule n'est que rarement utile).

Modèle:Bas de page