Mécanique du point/Oscillateurs
Oscillateur harmonique
Exemples d'oscillateurs
Masse-ressort : mouvement horizontal
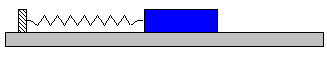
On considère un mobile auto porteur relié à un mur par un ressort de raideur k.
Bilan des forces :
- Une force de rappel due au ressort et proportionnelle au déplacement du mobile
- Le poids
- La réaction du support
On applique le principe fondamental de la dynamique au mobile :
On projette sur l'axe (Ox) :
On définie la pulsation propre de l'oscillateur :
On obtient une équation différentielle du second degré : Modèle:Encadre
Système Masse suspendue à un ressort
Bilan des forces :
- Poids
- Force de rappel du ressort :
Principe fondamental de la dynamique :
On projette sur l'axe à l'équilibre :
On introduit x l'écart par rapport à la position d'équilibre :
Équation caractéristique
Solution
On cherche si une solution de la forme peut convenir. Calculons ses dérivées par rapport au temps :
Introduisons ces expressions dans la partie gauche de l'équation caractéristique :
A est l'amplitude (en mètre) et la phase (en radian). Ces constantes sont déterminées grâce aux conditions initiales (Exemple).
La période propre du mouvement est la durée entre 2 passages consécutifs dans le même sens pour une position donnée. Une telle durée correspond à une augmentation de de l'argument de la fonction sinusoïdale et donc à
Ainsi :
La période est indépendante de l'amplitude du mouvement. Un tel système est dit isochrone.
Aspect énergétique
La vitesse est :
L'énergie cinétique est :
L'énergie potentielle est :
L'énergie mécanique est :
L'énergie mécanique est constante au cours du temps et proportionnelle au carré de l'amplitude.
avec
Oscillations amorties par un frottement fluide
En plus de la force de rappel, la particule est soumise à une force de frottement F=-bv. On applique le principe fondamental de la dynamique :
avec et
Le discriminant est :
Les solutions sont :