Logique séquentielle/Implantation matérielle avec bascules D et bascules JK

Réaliser un schéma séquentiel à partir d’un diagramme d'évolution consiste toujours à trouver une partie combinatoire. Les raisonnements seront séquentiels, mais les méthodes employées viennent du combinatoire : tables de vérité et tableaux de Karnaugh. On a appris au [[../Diagrammes d'évolution équations de récurrence/|chapitre précédent]] comment obtenir des équations de récurrence à partir des diagrammes d'évolution, dans ce chapitre nous allons présenter une étape supplémentaire : comment matérialiser des équations de récurrence ?

Implantations à l'aide de bascules D

Si l’on connaît les équations de récurrence, il est facile d'obtenir un schéma à l'aide de bascules D. Il suffit d'implanter ces équations de récurrence. Si on ne les connaît pas il suffit de les chercher. On présente d’abord ce que l’on cherche à réaliser : une partie combinatoire à la place du point d'interrogation :

Le travail que l’on cherche à réaliser

Et encore une fois, ce qui est important à comprendre, est le rôle de ce circuit combinatoire : calculer l'état futur à partir de l'état présent. On a évidemment utilisé le mot calculer dans un sens très large ici : il s'agit d’un calcul combinatoire, pas algébrique !

Modèle:Principe Ce principe doit devenir clair dans votre esprit si vous voulez comprendre. Nous savons par expérience que cela peut mettre plusieurs semaines à des étudiants (et à vous cher lecteur) pour cheminer dans vos têtes et y trouver une bonne place au chaud où personne ne viendra l'y déloger. Cette phrase est peut être un peu trop philosophique mais il faut bien se lâcher un peu, et en plus n’est pas cela l'apprentissage ?

Exemple

On cherche à implanter l'exemple du compteur du chapitre précédent. On a trouvé comme équations de récurrence :

Schéma complet d'implantation

$Q1=q1\oplus q0$

$Q0=\overline{q0}$

Et voici le schéma correspondant.

Remarquez comment on a utilisé le complément de Q0 en allant le chercher directement sur une sortie de bascule D. On rappelle que ce complément existe toujours en sortie d'une bascule D ou JK. Vous retrouvez donc bien vos deux équations dans votre schéma.

Exercice 1

Réaliser un compteur modulo 8 (qui compte de 0 à 7) à l'aide de 3 bascules. Modèle:Solution

Implantation à l'aide de bascules JK

Il faut utiliser le diagramme d'évolution de la bascule JK pour trouver les équations de récurrence sur J et sur K. Il y en a deux fois plus qu'avec des bascules D mais elles sont plus simples (pas à trouver mais à écrire).

Notre problème est encore une fois de trouver la partie combinatoire ci-dessous :

Comment remplir ce rectangle combinatoire ?

La méthode est présentée à l'aide d'une figure sur laquelle il faut passer un peu de temps pour bien la comprendre :

Nous avons voulu mettre tellement d'informations dans ce dessin qu'on a perdu en clarté et cela nécessite quelques explications que voici :

• Il y a 4 tableaux de Karnaugh parce qu’il y a 4 sorties à réaliser J1, K1, J0 et K0 (regardez la figure de principe ci-dessus et particulièrement le rectangle à construire).
• Lorsqu'on raisonne sur une transition donnée l'état de départ (état présent) détermine complètement la place dans les tableaux de Karnaugh à remplir (flèches rouges)
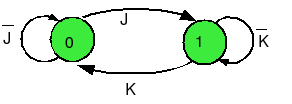
• la connaissance de l'état présent et de l'état futur permet à l'aide du diagramme d'évolution de la bascule JK (voir TD précédent rappelé ci-dessous) quelles sont les valeurs à positionner pour J et K des deux bascules. On en déduit ce qu’il faut mettre dans le tableau de Karnaugh.

Exercice 2

Réaliser la synthèse d’un diviseur de fréquence par trois à JK et à D.

Exercice 3

Réaliser un compteur modulo 9 avec trois bascules JK

Exercice 4

Réaliser un générateur de signaux carrés déphasés de 90°.