Introduction à l'électromagnétisme des milieux matériels/Circuits magnétiques

Qu'est-ce qu'un circuit magnétique ?

Pour bien aborder ce chapitre, nous allons faire de nombreuses analogies avec l'électrocinétique. À commencer par : comment définit-on un circuit électrique ? Comment marche-t-il ?

Prenons un exemple simple :

Un fil de cuivre

Ce circuit électrique est un système matériel dans lequel on est capable :

• de contrôler de l'énergie (l'énergie électrique)
• de la guider d'une source (la pile) vers des récepteurs (des lampes à incandescence)

Pour guider cette énergie électrique, qui est liée à un flux d'électrons, on utilise un matériau qui est un bon conducteur d'électricité (par exemple un fil de cuivre). Pour se déplacer, les électrons vont choisir bien évidemment le chemin le plus facile, c'est-à-dire suivre les fils de cuivre pour aller d'un point à un autre.

La philosophie pour un circuit magnétique est la même :

• On cherche à transporter de l'énergie sous forme magnétique.
• Cette énergie magnétique est véhiculée par un flux magnétique $\mathrm{\Phi }$.
• Pour canaliser ce flux, on a besoin d'un matériau avec une grande perméabilité magnétique. Ce sont très souvent des matériaux ferromagnétiques.
• Pour injecter de l'énergie dans le circuit magnétique, on va faire agir un magnétomoteur, c'est-à-dire que l’on va enrouler une bobine autour du matériau formant le circuit magnétique pour créer une source magnétomotrice.

Lorsqu'on fait circuler un certain courant dans la bobine, on excite le circuit à l'aide du magnétomoteur $𝔉=ni$. Un certain champ $H=\frac{𝔉}{l}$ s'installe. Si la perméabilité relative ${\mu }_r$ est choisie très grande devant 1, le flux $\mathrm{\Phi }$ sera essentiellement canalisé dans le circuit magnétique.

Modélisation d'un circuit magnétique

Notion de réluctance

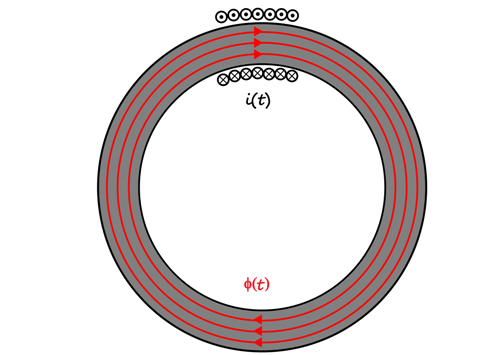
Étudions pour commencer le circuit magnétique ci-dessus :

• de section droite S
• autour duquel est enroulée d'une bobine de n spires parcourues par un courant i

Nous allons faire plusieurs approximations :

• Le circuit magnétique est parfait, c'est-à-dire que les lignes d'induction sont parfaitement canalisées dans le circuit magnétique (pas de fuites)
• Les lignes du champ induit sont réparties uniformément dans la section : $\mathrm{\Phi }=B\cdot S$

Appliquons le théorème d'Ampère à une ligne de champ orientée en concordance avec le champ induit :

$\begin{array}{cc}ni& ={\oint }_{𝒞}\overrightarrow{H}\cdot \mathrm{d}\overrightarrow{l}\\ & ={\oint }_{𝒞}\frac{\mathrm{\Phi }}{\mu S}\mathrm{d}l\end{array}$

Analogie avec les circuits électriques

On remarque alors une ressemblance forte entre les équations des circuits magnétiques et celles des circuits électriques :

Schémas équivalents

Circuits électriques	Circuits magnétiques

Grandeurs macroscopiques

Circuits électriques		Circuits magnétiques
Grandeur	Unité	Grandeur	Unité
Force électromotrice $e$	Volt V	Force magnétomotrice $𝔉=ni$	Ampère tour At
Intensité du courant électrique $I=\frac{e}{R}$	Ampère A	Flux magnétique $\mathrm{\Phi }=\frac{𝔉}{\Re }$	weber Wb
Résistance électrique $R=\frac{1}{\sigma }\frac{l}{S}$	ohm Ω	Réluctance magnétique $\Re =\frac{1}{\mu }\frac{l}{S}$	HenryModèle:Exp HModèle:Exp

Pour passer des grandeurs macroscopique, caractéristiques du circuit, à des grandeurs microscopiques, caractéristiques de la matière, on commence par diviser la force motrice par la longueur du chemin supposé homogène et on obtient donc le champ électrique (ou magnétique). Ensuite pour s'affranchir de la section du chemin on divise l'intensité du courant (ou le flux) par la section et on obtient la densité de courant (ou la densité de flux qui n'est autre que l'induction magnétique).

Grandeurs microscopiques

Circuits électriques		Circuits magnétiques
Grandeur	Unité	Grandeur	Unité
Champs électrique $E=\frac{e}{l}$	Volt par mètre VmModèle:Exp	Champ magnétique $H=\frac{𝔉}{l}$	Ampère tour par mètre AtmModèle:Exp
Densité de courant électrique $J=\frac{I}{S}$	Ampère par mètre carré AmModèle:Exp	Densité de flux ou Induction $B=\frac{\mathrm{\Phi }}{S}$	Weber par mètre carré ou Tesla T
Conductibilité électrique $\sigma =\frac{J}{E}$	Siemens par mètre SmModèle:Exp	Perméabilité magnétique $\mu =\frac{B}{H}$	Henry par mètre HmModèle:Exp

Modèle:Attention

En effet, en électricité, la résistance R représente un phénomène de résistance de passage au courant, et donc de dissipation d'énergie sous forme de chaleur, ce qui n’est pas du tout le cas de la réluctance $\Re$ qui ne chauffe pas !

La densité de courant J est à l'origine de la fusion du conducteur (fusibles). La densité de flux (ou l'induction B) est à l'origine d'une saturation éventuelle sans destruction du chemin magnétique. Une induction trop forte fait progressivement tendre ${\mu }_r$ vers 1, le matériau perd ses propriétés ferromagnétiques.

Exemple : un fusible cylindrique va fondre à 30 A/mmModèle:Exp, un matériau ferromagnétique va se saturer à 1 T.

Auto-induction

Coefficient d’auto-induction

On appelle coefficient de self induction ou d’auto-induction le coefficient L qui relie la fem e(t) et variation du courant dans une bobine :

$e(t)=L\frac{di(t)}{dt}$

De la même manière que C est le coefficient qui relie le courant à la variation de la différence de potentiel aux bornes d’un condensateur.

$i(t)=C\frac{de(t)}{dt}$

Ces deux dernières expressions étant tout simplement la loi d'ohm généralisée.

$e(t)=Ri(t)$

Cette dernière relation est d'une grande importance pratique. En effet la mesure de L, qui est une quantité purement électrique, est aussi une mesure indirecte de $\Re$. Ceci s'avère très utile pour évaluer la valeur de la réluctance, en particulier en présence d'entre fer où le flux s'évase toujours plus ou moins et où le calcul est assez compliqué.

La réluctance magnétique $\Re ={\frac{1}{\mu }}_0\frac{l}{S}={\frac{1}{\mu }}_0\frac{l}{\pi {𝔯}^2}$

L'inductance $L=\frac{n^2}{\Re }=\frac{n^2{\mu }_0\pi {𝔯}^2}{l}$

Méthode de mesure de L

Il suffit donc de retrancher à $u(t)$, tension aux bornes de la bobine, les chutes ohmiques $Ri(t)$ pour remonter à $e(t)$. Ayant mesuré $i(t)$ et sa dérivée $\frac{di(t)}{dt}$, L est tout simplement le rapport $L=\frac{e(t)}{di(t)/dt}$.

Méthode de mesure de L

Schéma	Réponse

Cette méthode est applicable en tous point de la réponse $i(t)$ et présente donc l’intérêt majeur de pouvoir faire une mesure autour du point $I_0$ d’utilisation prévu pour $L$. Sachant que $L$ est une fonction de $i$ en présence d'un noyau en fer doux, revoir les courbes $B(H)$ pour justification, il est alors possible de faire une mesure au point précis d’utilisation.