Généralités sur les fonctions/Exercices/Lecture graphique d'images et d'antécédents

Exercice 4-1

Lecture graphique d'images

a) Lire graphiquement $f(2)$. Traduire par une phrase en français.

b) Lire graphiquement $f(4)$. Peut-on savoir s'il s'agit d'une valeur exacte ? Justifier.

c) Lire graphiquement $f(3)$. Peut-on savoir s'il s'agit d'une valeur exacte ? Justifier.

d) Lire graphiquement $g(7,5)$. Peut-on savoir s'il s'agit d'une valeur exacte ? Justifier.

e) Lire graphiquement $g(5)$ et $f(5)$. Traduire par une phrase en français.

f) Lire graphiquement $g(8)$ et $f(8)$. Traduire par une phrase en français.

Exercice 4-2

Lecture graphique d'images

a) $f(2)=$

Traduire par une phrase en français.

b) Lire graphiquement $f(0)=...$, $f(4)=...$, $f(5)=...$,$f(6)=...$, $f(7)=...$, $f(8)=...$, $f(9)=...$.

c) Présenter ces résultats (ne pas oublier celui du a)) dans un tableau de valeurs :

x	0
$f(x)$

d) $g(2)=$

Traduire par une phrase en français.

e) Lire graphiquement $g(0)=...$, $g(4)=...$, $g(5)=...$, $g(6)=...$, $g(7,5)=...$, $g(8)=...$, $g(9)=...$.

f) Présenter ces résultats (ne pas oublier celui du d)) dans un tableau de valeurs :

x	0
$g(x)$

Exercice 4-3

Lecture graphique d'antécédents

a) Donner par lecture graphique les antécédents de 1 par $g$.

b) Donner par lecture graphique les antécédents de 2 par $f$.

c) Donner par lecture graphique les antécédents de 3 par $g$.

d) Donner par lecture graphique les antécédents de 4 par $f$.

e) Donner par lecture graphique les antécédents de –3 par $f$.

f) Donner par lecture graphique les antécédents de –2 par $f$.

g) Donner par lecture graphique les antécédents de –1 par $g$. Modèle:Solution

Exercice 4-4

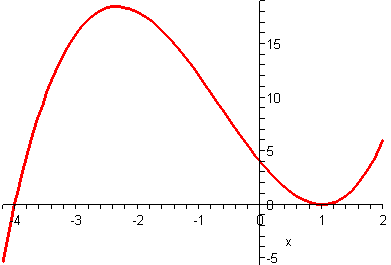
La courbe ci-dessous représente une fonction f définie sur [–4, 2].

a) Par lecture graphique, donner le tableau de variations de f.

b) Par lecture graphique, donner une valeur approchée au dixième de f(–2).

c) Par lecture graphique, donner une valeur approchée à l'unité des antécédents de 2 par f.

d) Soit k un réel quelconque. Discuter en fonction de k le nombre de ses antécédents par f. Modèle:Solution