Dynamique/Annexe/Outils mathématiques pour la dynamique

On présente ici quelques outils mathématiques nécessaires à la compréhension du cours de dynamique. Il s'agit plus d'un formulaire, d'un aide-mémoire, que d'un cours de mathématiques : les notions présentées ici le sont de façon plutôt aride et aucun résultat n'est démontré. Il vaut mieux pour le lecteur complètement novice de suivre un cours de mathématique plutôt que de se contenter de la lecture de ce chapitre. En particulier, on ne mentionne pas ici la théorie de la projection de vecteurs, qui a été largement rappelée lors du cours de dynamique.

Nombres complexes

Définitions, écriture algébrique d'un nombre complexe

On suppose le lecteur familier avec les nombres réels et leurs propriétés. On appelle nombre complexe tout nombre du type $a+ib$, avec $a$ et $b$ deux réels quelconques, et $i$ un nombre (non réel) vérifiant $i^2=-1$. L'ensemble des nombres complexes est noté $𝐂$. À partir de là, on calcule avec les nombres complexes comme avec les nombres réels, en remplaçant $i^2$ par $-1$ à chaque fois qu'on le rencontre dans les calculs. Dans l'écriture $z=a+ib$, $a$ est appelé la partie réelle de $z$, alors que $b$ est appelé la partie imaginaire de $z$. Un nombre complexe admet une et une seule partie réelle, et une et une seule partie imaginaire. Ce qui signifie qu'une égalité dans les nombres complexes du style $a+ib=c+id$ est équivalente à ce système :

$$\{\begin{array}{c}a=c\\ b=d\end{array}$$Si $z=a+ib$, l'écriture $a+ib$ est appelée écriture algébrique de $z$. On appelle conjugué de $z$ le complexe $\bar{z}=a-ib$ et on a alors $|z|=\sqrt{z\bar{z}}$

On a alors $\frac{1}{z}=\frac{\bar{z}}{z\bar{z}}=\frac{\bar{z}}{|z{|}^2}$

Représentation géométrique, écriture trigonométrique et exponentielle complexe

Chaque nombre complexe peut être vu comme un point d'un plan, appelé plan complexe.

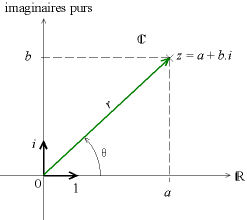
Les nombres complexes peuvent être interprétés comme des points d'un plan particulier qu'on appelle le plan complexe. On appelle alors module (ou norme) d'un nombre complexe $z=a+ib$ la distance qui le sépare de l'origine du plan, que l'on note $|z|$ On a, par le théorème de Pythagore, $|z|=\sqrt{a^2+b^2}$

On définit un argument de $z$ comme une mesure de l'angle formé par l'axe des abscisses et la droite passant par l'origine et par le point d'affixe $z$ (c'est l'angle $\theta$ sur la figure ci-contre)

À partir de là, tout nombre complexe s'écrit de façon unique sous la forme $z=\rho (\cos \theta +i\sin \theta )$, avec $\theta \in [0;2\pi ]$ et $\rho =|z|$

Cette écriture est appelée écriture trigonométrique d'un nombre complexe.

Pour tout $\theta \in 𝐑$, on pose $e^{i\theta }=\cos \theta +i\sin \theta$

À partir de là, on vérifie aisément que

• $\mathrm{\forall }\theta \in 𝐑,|e^{i\theta }|=1$
• $\mathrm{\forall }(\theta ,{\theta }^{\prime })\in {𝐑}^2,e^{i\theta }{e}^{i{\theta }^{\prime }}=e^{i(\theta +{\theta }^{\prime })}$
• $\mathrm{\forall }\theta \in 𝐑,{\left(e^{i\theta }\right)}^{-1}=\overline{e^{i\theta }}=e^{-i\theta }$

Équations différentielles linéaires (EDL)

Qu'est-ce qu'une EDL

Une équation différentielle est un cas particulier d'équation fonctionnelle. Une équation fonctionnelle est une équation où l'inconnue n'est plus un nombre mais une fonction. Une équation différentielle est une équation fonctionnelle où la fonction inconnue est liée à sa dérivée (et, éventuellement, à la dérivée de sa dérivée, etc). Par exemple, l'équation $y^{″}(x)+\ln (y^{\prime }(x))+2xy(x)=\exp (-x^2)\sin (x)$ est une équation différentielle d'inconnue $y$.

Une équation différentielle linéaire est une équation différentielle de la forme $a_n{y}^{(n)}(x)+\cdots +a_1{y}^{\prime }(x)+a_{0}y(x)=f(x)$, et $n$ est alors appelé l'ordre de l'équation différentielle linéaire.

Éléments d'algèbre et d'analyse vectorielle

Notion de vecteur

En physique, un vecteur peut être vu comme un objet mathématique pouvant modéliser une translation dans l'espace (ou le plan). Il est entièrement caractérisé par la donnée d'une direction, d'un sens et d'une norme, ou par la donnée de ses trois composantes spatiales.

On peut également le caractériser par la donnée d'un point et du point en lequel est transformé ce premier point après la translation. Ainsi, si un point $A$ est translaté par un certain vecteur vers un point $B$, ce vecteur sera noté $𝐀𝐁$. Si l'on dispose des coordonnées de ces points, on peut déterminer les coordonnées de $𝐀𝐁$ par $𝐀𝐁=\left(\begin{array}{c}{x}_B-x_A\\ y_B-y_A\\ z_B-z_A\end{array}\right)$

Déterminons enfin par un point de typographie trop méconnu. Lorsque l'on écrit sur un ordinateur, on note les vecteurs en gras ($𝐮$). On ne les note en police classique surmontée d'une flèche ($\overrightarrow{u}$) que lorsque l'on écrit en manuscrit.

Algèbre vectorielle

L'algèbre vectorielle est l'étude des opérations définie sur l'ensemble des vecteurs.

Somme, multiplication par un scalaire, différence de deux vecteurs

Soit deux vecteur $𝐮=\left(\begin{array}{c}x\\ y\\ z\end{array}\right)$ et $𝐯=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right)$et un réel $\lambda$. On a $𝐮\mathbf{+}𝐯=\left(\begin{array}{c}x+x^{\prime }\\ y+y^{\prime }\\ z+z^{\prime }\end{array}\right)$, $\lambda 𝐮=\left(\begin{array}{c}\lambda x\\ \lambda y\\ \lambda z\end{array}\right)$ et $𝐮-𝐯=𝐮+(-𝐯)=\left(\begin{array}{c}x-x^{\prime }\\ y-y^{\prime }\\ z-z^{\prime }\end{array}\right)$

L'addition est commutative, ce qui signifie que $𝐮+𝐯=𝐯+𝐮$

L'addition est associative, ce qui signifie que $𝐮+(𝐯+𝐰)=(𝐮+𝐯)+𝐰$

On a la fameuse relation de Chasles, $𝐀𝐁+𝐁𝐂=𝐀𝐂$

De plus, on a $\lambda (𝐮+𝐯)=\lambda 𝐮+\lambda 𝐯$

Produit scalaire

Le produit scalaire de deux vecteurs $𝐮$ et $𝐯$ est définie par $𝐮.𝐯=\Vert 𝐮\Vert \times \Vert 𝐯\Vert \times \cos (𝐮;𝐯)$. De plus, si $𝐮=\left(\begin{array}{c}x\\ y\\ z\end{array}\right)$ et $𝐯=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right)$, alors $𝐮.𝐯=x{x}^{\prime }+y{y}^{\prime }+z{z}^{\prime }$

Deux vecteurs sont orthogonaux si, et seulement si, $𝐮.𝐯=0$

Le produit scalaire est commutatif et distributif par rapport à l'addition vectorielle.

De plus, $𝐮.𝐮=\Vert u{\Vert }^2$

Analyse vectorielle

L'analyse vectorielle est l'étude des fonctions qui prennent en paramètre des vecteurs, renvoie des vecteurs, ou les deux à la fois. L'analyse vectorielle n'est pas très utile en dynamique (elle l'est beaucoup plus en électromagnétisme), aussi n'y présentons-nous que des rudiments.

Soit une fonction $f$ à trois variables (les trois coordonnées de l'espace) renvoyant un scalaire. On appelle gradient de $f$, que l'on note $𝐠𝐫𝐚𝐝f$, la fonction $\frac{\partial f}{\partial x}{𝐞}_x+\frac{\partial f}{\partial y}{𝐞}_y+\frac{\partial f}{\partial z}{𝐞}_z$. Il s'agit d'une fonction vectorielle.

Il est important de remarquer que l'expression donnée ici du gradient est l'expression en coordonnées cartésiennes. Cependant, à l'aide de cette expression on remarque que $\text{d}f=𝐠𝐫𝐚𝐝f\times \text{d}𝐫$. Ceci est la définition intrinsèque du gradient (c'est la définition proposée en générale dans les livres), qui ne dépend pas du système de coordonnées. À partir de là on peut en déduire le gradient en coordonnées cylindriques et sphériques.

Gradient en coordonnées cylindriques : $𝐠𝐫𝐚𝐝f=\frac{\partial f}{\partial r}{𝐞}_r+\frac{1}{r}\frac{\partial f}{\partial \theta }{𝐞}_{\theta }+\frac{\partial f}{\partial z}{𝐞}_z$

Gradient en coordonnées sphériques : $𝐠𝐫𝐚𝐝f=\frac{\partial f}{\partial r}{𝐞}_r+\frac{1}{r}\frac{\partial f}{\partial \theta }{𝐞}_{\theta }+\frac{1}{r\sin \theta }\frac{\partial f}{\partial \phi }{𝐞}_{\phi }$

Développements limités usuels

Les résultats suivants permettent de faire des approximations lorsque les calculs deviennent trop lourds ou ingérables. Ils ne sont vrais qu'au voisinage de zéro.

$\exp (x)\approx 1+x$

$\cos (x)\approx 1$ ou $\cos (x)\approx 1+\frac{x^2}{2}$ si l'on souhaite plus de précision

$\sin (x)\approx x$

$\tan (x)\approx x$

$(1+x{)}^{\alpha }\approx 1+\alpha x$ ou $(1+x{)}^{\alpha }\approx 1+\alpha x+\alpha (\alpha -1)\frac{x^2}{2}$ si l'on souhaite plus de précisions

Modèle:Bas de page