Calcul avec les nombres complexes/Écriture exponentielle et trigonométrique
Il existe une seconde forme d'écriture des complexes.
L'écriture exponentielle d’un nombre complexe permet d'extraire du premier coup d’œil son module et son argument, et permet aussi de mémoriser plus aisément les propriétés vues dans le chapitre précédent sur les modules et les arguments.
Notation exponentielle
Formule d'Euler
Modèle:Définition Voir l'annexe « [[../Annexe/Démonstration de la formule d'Euler|Démonstration de la formule d'Euler]] ».
Écriture exponentielle
Pour tout nombre complexe non nul, de module et d'argument principal , on a : .
Reconnaître un nombre complexe sous sa forme exponentielle
Conjugué
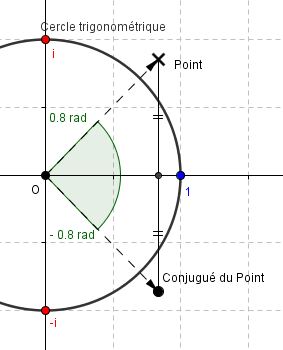 |
Exemple
Propriétés des arguments et des modules
Soit z et z' deux nombres complexes non nuls sous la forme exponentielle : et avec et .
Nous allons maintenant revoir toutes les propriétés des arguments et des modules du chapitre précédent, qui seront maintenant plus faciles à comprendre et à se souvenir grâce à la notation exponentielle.
Produit
 |
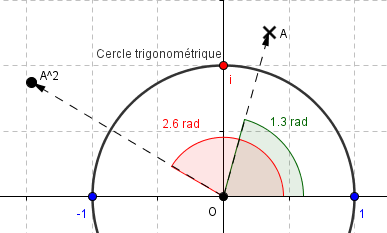 |
 |
Inverse et division
 |
 |
Puissance
Exemples
Calculer le cosinus et le sinus d’un angle
On peut aussi utiliser ces propriétés pour calculer exactement un cosinus ou un sinus d’un angle .
Pour cela, il suffit juste de connaître deux angles a et b dont leur somme est égale à , et de connaître leurs cosinus et sinus.
Voici ensuite la démarche à suivre :
- On a et on connaît , , et .
- Pour simplifier, on prend un module de 1 (les points sont sur le cercle trigonométrique).
- Formule d'Euler : .
- .
- Trouver les valeurs algébriques (cartésiennes) des deux nombres complexes qui correspondent à un module de 1 et à un argument respectivement de a et de b :
et . La réussite de l'exercice dépend de cette étape. - Multiplier ces deux nombres complexes sous leur forme algébrique : .
- .
- On identifie, en séparant les parties réelles et imaginaires :
et .
Ce qui nous amène à traiter le cas général : les formules d'addition des cosinus et des sinus.
Formules d'addition des cosinus et sinus
Ce résultat est à mettre en relation avec le produit de deux nombres complexes : . On peut ainsi se souvenir des formules d'addition en remplaçant les x par des cos, les y par des sin, et bien sûr avec !
Cette méthode permet aussi de retrouver par exemple ou encore , en développant des formules plus compliquées.

