Amplificateur opérationnel/Montage amplificateur inverseur

Dans cette partie, nous étudions un circuit dont la configuration est la suivante :

On fera deux études :

L'une reposant sur le modèle de l'amplificateur inverseur idéal.
Puis on utilisera le modèle non-idéal

Amplificateur opérationnel idéal

L'étude de circuits contenant des amplificateurs peut être simplifiée en prenant en compte deux propriétés de l'amplificateur idéal:

$A = \infty$
Les résistances d'entrée sont infinies : les courants entrant par les bornes inverseuse et non-inverseuse de l'amplificateur sont nuls.

La première propriété implique que les potentiels à chaque borne doivent être égaux:

$v^{+} - v^{-} = \frac{V_{s}}{A} = 0$

Donc, dans le circuit étudié, cela implique $v^{-} = 0 V$ parce que $v^{+}$ est à la masse du circuit.

Bien entendu, dans la réalité, $v^{+}$ et $v^{-}$ ne peuvent pas être égaux, car l'amplificateur n'effectuerait aucune opération. Cependant, comme $A$ est très grand, la différence est très petite et on peut donc la négliger.

On calcule alors la fonction de transfert. Soit $i$ le courant parcourant les deux résistances, orienté (arbitrairement) de l'entrée vers la sortie. Comme les résistances d'entrées sont infinies, le même courant parcourt $R_{1}$ et $R_{2}$ . Il en découle :

$V_{e} = R_{1} i$ et $V_{s} = - R_{2} i$ , soit $\begin{matrix} \frac{V_{s}}{V_{e}} & = - \frac{R_{2}}{R_{1}}, \end{matrix}$

On verra plus tard que l'influence de la fréquence sur $A$ oblige à examiner plus prudemment le comportement du circuit lorsque la fréquence du signal d'entrée est plus élevée (en dehors de la gamme de fréquence dans laquelle $A$ peut être considéré constant).

Amplificateur opérationnel non idéal

On peut développer les deux équations reliant la tension de sortie $v_{s}$ à la tension d'entrée $v_{e}$ . La première d'entre elles peut être trouvée par le théorème de superposition:

(Remarque : l'utilisation du théorème de superposition présuppose que le même courant traverse le deux résistances, soit encore que les résistances d'entrée de l'AO sont infinies.

$v^{-} = \frac{R_{2}}{R_{1} + R_{2}} V_{e} + \frac{R_{1}}{R_{1} + R_{2}} V_{s} .$

On déduit la seconde du fonctionnement de l'amplificateur opérationnel:

$V_{s} = A (v^{+} - v^{-}) .$

On peut noter que $v^{+} = 0$ et résoudre la seconde équation à partir de $v^{-}$ :

$v^{-} = - \frac{V_{s}}{A} .$

On réinjecte ensuite cette équation dans l'autre et on obtient:

$- \frac{V_{s}}{A} = \frac{R_{2}}{R_{1} + R_{2}} V_{e} + \frac{R_{1}}{R_{1} + R_{2}} V_{s} .$

On soustrait $\frac{R_{1}}{R_{1} + R_{2}} V_{s}$ des deux cotés de l'équation et on factorise $v_{s}$ à gauche.

$- (\frac{1}{A} + \frac{R_{1}}{R_{1} + R_{2}}) V_{s} = \frac{R_{2}}{R_{1} + R_{2}} V_{e} .$

On divise l'équation par $\frac{1}{A} + \frac{R_{1}}{R_{1} + R_{2}}$ et par $V_{e}$ afin de faire ressortir le gain du montage. On obtient alors :

$G = \frac{V_{s}}{V_{e}} = - \frac{\frac{R_{2}}{R_{1} + R_{2}}}{\frac{1}{A} + \frac{R_{1}}{R_{1} + R_{2}}}$

On réécrit de façon plus claire l'équation en multipliant par $R_{1} + R_{2}$ le numérateur et le dénominateur :

$G = - \frac{R_{2}}{\frac{(R_{1} + R_{2})}{A} + R_{1}} .$

Si $A$ est très grand, le premier terme du dénominateur peut être négligé, ce qui donne pour le gain :

$G = \frac{V_{s}}{V_{e}} \approx - \frac{R_{2}}{R_{1}} .$

On démontre ainsi le fait que le gain d'amplification $A$ disparaît de la formule du gain du montage (du fait de sa valeur relativement élevée). Le gain du circuit n'est déterminé que par les éléments extérieurs du montage.
La conséquence de la variation de la valeur de $A$ suivant les constructeurs est donc moindre (remarque ???? bien au contraire !!) . Tant que $A$ reste relativement élevé, l'approximation reste raisonnable.

On trouve le même résultat que précédemment, mais l'hypothèse du fonctionnement idéal de l'AOP a permis de simplifier considérablement l'étude. Généralement, supposer l'amplificateur idéal permet d’avoir une idée générale du fonctionnement du circuit.
On vient d'étudier ici le montage amplificateur inverseur. Il est appelé inverseur car le signe de la tension de sortie est l'inverse de celui de la tension d'entrée. La valeur du gain du montage est déterminée par le rapport $\frac{R_{2}}{R_{1}}$ et peut être plus grand ou plus petit que 1.

Impédance de sortie

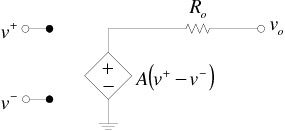
Jusqu'à maintenant, on a toujours considéré que l'impédance de sortie d'un amplificateur opérationnel était nulle. L'impédance de sortie typique d'un amplificateur opérationnel tel que le LM741 est d'environ Modèle:Unité. Un modèle plus proche de la réalité serait une source de tension contrôlée avec une résistance de sortie notée $R_{o}$ . On obtient donc le modèle suivant de l'AOP:

Pour calculer l'impédance de sortie dans le montage amplificateur inverseur, on met à zéro la tension en entrée (c'est-à-dire que la source de tension en entrée est remplacée par un court-circuit, ici on néglige sa résistance interne) et on applique une tension "test" sur la sortie du montage puis on calcule le courant "entrant par la sortie". Il ne reste plus qu’à appliquer la loi d'Ohm afin de trouver l'impédance. On obtient au final un montage comme celui-ci :

En négligeant le courant rentrant par l'entrée de l'amplificateur opérationnel, on peut calculer la valeur du courant traversant la résistance $R_{1}$ :

$i_{R_{1}} = \frac{v_{t e s t}}{R_{1} + R_{2}} .$

On peut aussi calculer la valeur du courant traversant la résistance $R_{o}$ :

$\begin{matrix} i_{R_{o}} & = \frac{v_{t e s t} - A (v^{+} - v^{-})}{R_{o}} \\ = \frac{v_{t e s t} + A v^{-}}{R_{o}} . \end{matrix}$

car $v^{+} = 0$

On additionne ces deux courants :

$\begin{matrix} i_{t e s t} & = \frac{v_{t e s t}}{R_{1} + R_{2}} + \frac{v_{t e s t} + A v^{-}}{R_{o}} . \end{matrix}$

La valeur $v^{-}$ est donnée par $v^{-} = i_{R_{1}} R_{1}$ , donc :

$\begin{matrix} i_{t e s t} & = \frac{v_{t e s t}}{R_{1} + R_{2}} + \frac{v_{t e s t} + A i_{R_{1}} R_{1}}{R_{o}} \\ = \frac{v_{t e s t}}{R_{1} + R_{2}} + \frac{v_{t e s t} + A \frac{v_{t e s t}}{R_{1} + R_{2}} R_{1}}{R_{o}} \\ = (\frac{1}{R_{1} + R_{2}} + \frac{1}{R_{0}} + A \frac{R_{1}}{R_{0} (R_{1} + R_{2})}) v_{t e s t} \\ R_{o u t} & = \frac{v_{t e s t}}{i_{t e s t}} = \frac{1}{\frac{1}{R_{1} + R_{2}} + \frac{1}{R_{0}} + A \frac{R_{1}}{R_{0} (R_{1} + R_{2})}} . \end{matrix}$

Pour des grandes valeurs de $A$ le troisième terme du dénominateur est prépondérant par rapport aux deux autres, ce qui rend $R_{o u t}$ bien plus petite que $R_{o}$ , impédance de sortie de l'amplificateur.

Cette étude montre que le grand avantage d’utiliser un amplificateur opérationnel est la possibilité de construire des montages de très faible impédance de sortie. Cela implique aussi que lorsque l’on connecte ce montage à l'entrée d'un autre, le signal présent à l'entrée du deuxième montage n'est que faiblement atténué.

Impédance d'entrée

$Z_{e} = R_{1}$

Modèle:Bas de page

Amplificateur opérationnel/Montage amplificateur inverseur

Sommaire

Amplificateur opérationnel idéal

Amplificateur opérationnel non idéal

Impédance de sortie

Impédance d'entrée

Menu de navigation

Amplificateur opérationnel/Montage amplificateur inverseur

Amplificateur opérationnel idéal

Amplificateur opérationnel non idéal

Impédance de sortie

Impédance d'entrée

Menu de navigation

Rechercher