Triangles et parallèles/Exercices/Théorème de Thalès
Exercice
NAC est un triangle. On suppose que :
- (PM) est parallèle à (AC) ; (RS) est parallèle à PM ;
- P appartient à [AN]; M appartient à [CN]; R appartient à [MC]; S appartient à [PA] ;
- NM = Modèle:Unité ; NC = Modèle:Unité ; NP = Modèle:Unité.
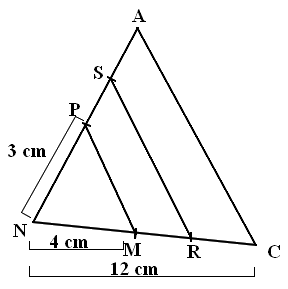
1. Écrire toutes les égalités qui résultent de la propriété des 3 rapport égaux en précisant le triangle concerné.
2. Calculer la longueur PA.
Exercice
Démonstration : À un tiers de sa hauteur, une pyramide occupe deux tiers de son volume total
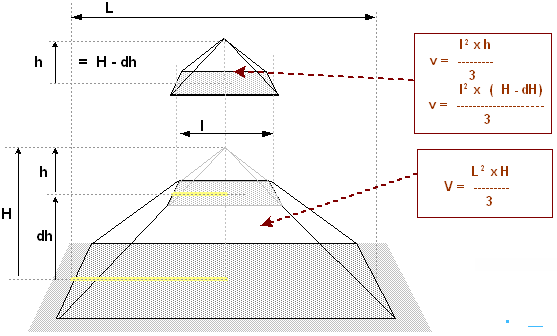
Rappel sur le calcul du volume d'une pyramide
Le volume d'une pyramide de hauteur , dont la largeur de la base est , est :
L'évolution du volume de la pyramide revient à tronquer celle-ci par une plus petite partant du sommet
Partons du schéma ci-dessous
Dans le schéma, le volume de la grande pyramide vaut , et celui de la petite pyramide vaut
La hauteur de la pyramide tronquée peut s'obtenir à partir des hauteurs des deux pyramides par la formule :
On peut alors exprimer le pourcentage d’évolution de la pyramide par :
- .
Du coup
Si on fait varier la hauteur de la petite pyramide de cette manière alors varie comme suit et varie comme suit
Application du théorème de Thalès à la pyramide
On peut appliquer le théorème de Thalès dans le schéma et relier les dimensions des deux pyramides. On obtient :
Donc on peut exprimer à partir de et de comme suit ou encore
Le remplissage de la pyramide tronquée est donc
Ce qui donne
Soit encore
L’évolution du remplissage de la pyramide tronquée est égal à
À un tiers de sa hauteur, le volume rempli de la pyramide est donc de : , soit très proche de
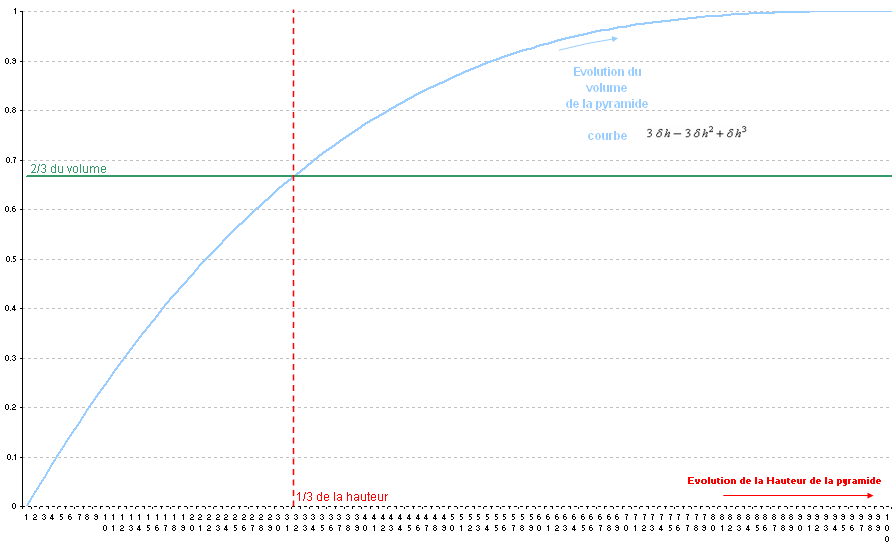
Démonstration graphique
Si on trace la courbe on peut voir effectivement qu’à un tiers de sa hauteur, il y a deux tiers du volume d'une pyramide