Dynamique/Énergétique du point matériel

L’énergétique est l’étude de l’énergie d'un corps, de ses différentes formes et de son échange avec le milieu extérieur.

L’énergie est une grandeur définie à l’aide du principe de conservation : par définition, l’énergie est une grandeur qui se conserve à l’échelle de l’Univers. L’Univers tout entier possède une certaine quantité d’énergie censée ne jamais varier. Nous étudierons alors des résultats de conservation de l’énergie en mécanique, mais également de non-conservation (si l’énergie de l’Univers est censée se conserver, rien n’interdit de penser que l’énergie d'un certain système particulier ne se conserve pas, et est transférée vers un autre système).

L'étude de l'énergie sera également l'occasion pour nous d'énoncer et de démontrer de nouveaux théorèmes de mécanique, qui rendront plus simple la résolution de certains problèmes de mécanique.

Puissance et travail d'une force

Soit un point matériel $M$ de masse $m$ soumis à une force $𝐅$ et se déplaçant à une vitesse $𝐯$ dans un référentiel donné. La puissance de cette force est, par définition, la grandeur $𝒫(𝐅)=𝐅.𝐯$

Il est important de remarquer que la puissance dépend du référentiel (puisque la vitesse en dépend)

Le travail élémentaire de $𝐅$ est, par définition, la grandeur $\delta W=𝒫(𝐅)\text{d}t=𝐅.𝐯\text{d}t=𝐅.\text{d}𝐎𝐌$ (la dernière égalité provenant du fait que $𝐯=\frac{\text{d}𝐎𝐌}{\text{d}t}$)

Le travail total entre deux points $A$ et $B$ est égal à ${𝒲}_{A\to B}=\underset{A}{\overset{B}{\int }}𝐅.\text{d}𝐎𝐌=\underset{A}{\overset{B}{\int }}𝐅.𝐯\text{d}t$

Le travail représente l'énergie que cède une force à un système. Si ce travail est positif, la force cède effectivement de l'énergie au système. Si ce travail est négatif, la force retire de l'énergie au système, et, ce faisant, s'oppose au mouvement. On parle alors de travail résistif.

Il est noté $\delta W$ et non pas $\text{d}W$ car il ne s'agit pas de la variation infinitésimale d'une fonction : contrairement, par exemple, à la vitesse que l'on peut définir en chaque instant et pour laquelle on peut donc représenter $\text{d}𝐯$ (qui est, en gros, égal à $𝐯(t+\epsilon )-𝐯(t)$ quand $\epsilon$ devient petit), on ne peut pas faire cela pour le travail car le travail, par définition, n'est pas une grandeur instantanée : c'est une grandeur qui symbolise la variation d'énergie entre deux instants (qui peuvent, éventuellement, être infiniment proches). C'est une grave erreur que d'écrire $\text{d}W$, car cette erreur dénote un problème conceptuel : l'étudiant qui commet cette erreur n'a pas compris la définition du travail.

Énergie cinétique et théorèmes s'y rapportant

L'énergie cinétique est une grandeur que l'on note ${ℰ}_K$ (K pour "κινετικος", "kinêtikos", mot grec signifiant "cinétique") ou ${ℰ}_C$ et qui est égal, par définition, à $\frac{1}{2}m{v}^2$

Remarquons, une fois de plus, que cette grandeur dépend du référentiel, puisque la vitesse en dépend (même si cette dépendance n'est ici pas notée, pour ne pas alourdir les notations)

Théorème de la puissance cinétique

Considérons un point matériel $M$ de masse $m$ constante soumis à $\sum _i{𝐅}_i$ et évoluant à une vitesse $𝐯$ dans un référentiel galiléen $ℛ$. On peut donc appliquer la deuxième Loi de Newton qui donne $m\frac{\text{d}𝐯}{\text{d}t}=\sum _i{𝐅}_i$

Multiplions scalairement cette relation par $𝐯$. On obtient

$m\frac{\text{d}𝐯}{\text{d}t}𝐯=\sum _i{𝐅}_i.𝐯$

Or $m𝐯\frac{\text{d}𝐯}{\text{d}t}=m\frac{\text{d}}{\text{d}t}\left(\frac{1}{2}{𝐯}^2\right)=m\frac{\text{d}}{\text{d}t}\left(\frac{1}{2}{v}^2\right)=\frac{\text{d}}{\text{d}t}\left(\frac{1}{2}m{v}^2\right)$ (la première égalité s'obtenant grâce à la formule de dérivation d'une composée), et nous aboutissons donc à l'énoncé du théorème de la puissance cinétique : $$\frac{\text{d}{ℰ}_K}{\text{d}t}=\sum _i𝒫({𝐅}_i)$$

Théorème de l'énergie cinétique

Considérons un point matériel $M$ de masse $m$ constante soumis à $\sum _i{𝐅}_i$ et évoluant à une vitesse $𝐯$ dans un référentiel galiléen $ℛ$. On peut donc appliquer le théorème de la puissance cinétique, qui donne $\frac{\text{d}{ℰ}_K}{\text{d}t}=\sum _i𝒫({𝐅}_i)$, soit $\text{d}{ℰ}_K=\sum _i𝒫({𝐅}_i)\text{d}t=\sum _i\delta W({𝐅}_i)$, et, en intégrant entre $A$ et $B$, nous aboutissons à l'énoncé du théorème de l'énergie cinétique$$\mathrm{\Delta }{ℰ}_K=\sum _i{𝒲}_{A\to B}({𝐅}_i)$$

Énergie mécanique et théorèmes s'y rapportant

Notion de force conservative et d'énergie potentielle

Une force est dite conservative si son expression dépend uniquement de la position du point. Par exemple, la force de gravitation terrestre ${𝐅}_{grav}=-𝒢\frac{m{M}_T}{d^2}{𝐞}_{𝐫}$ est conservative, car elle ne dépend que de la position du point. Par contre, la force de frottement linéaire $𝐅=-\alpha 𝐯$ dépend de la vitesse, et n'est donc pas conservative.

Il existe alors une certaine fonction d'état ${ℰ}_p$ telle que $\text{d}{ℰ}_p=-\delta W$ (ce résultat est à admettre, il se démontrerait en mathématique avec des outils de calcul différentiel très poussés). En intégrant, on obtient alors $\mathrm{\Delta }{ℰ}_p=-{𝒲}_{A\to B}(𝐅)$ : il faut donc comprendre que cette fonction n'est définie qu'à une constante arbitraire près, et que seul $\mathrm{\Delta }{ℰ}_p$ (ou $\text{d}{ℰ}_p$) a un sens physique.

Nous avons donc établi que $\text{d}{ℰ}_p=-\delta W=-𝐅.\text{d}𝐎𝐌$. En utilisant la définition intrinsèque du gradient, il vient $𝐅=-𝐠𝐫𝐚𝐝({ℰ}_p)$

Notion d'énergie mécanique

Soit un point matériel $M$ de masse $m$ soumis à $\sum _i{𝐅}_i$, dont certaines sont conservatives (et admettent donc une énergie potentielle). On appelle énergie mécanique la grandeur ${ℰ}_m={ℰ}_c+\sum _i{ℰ}_{pi}$ où ${ℰ}_{pi}$ désigne la $i^{\stackrel{`}{e}me}$ énergie potentielle associée à la $i^{\stackrel{`}{e}me}$force conservative.

Théorème de l'énergie mécanique

Considérons un point matériel $M$ de masse $m$ constante soumis à $\sum _i{𝐅}_i$ (dont certaines sont conservatives) et évoluant à une vitesse $𝐯$ dans un référentiel galiléen $ℛ$.

On note $\sum _i{𝐅}_i=\sum {𝐅}^c+\sum {𝐅}^{nc}$ où ${𝐅}^c$ désigne une force conservative et ${𝐅}^{nc}$ une force non conservative.

On peut appliquer le théorème de l'énergie cinétique, qui donne $\mathrm{\Delta }{ℰ}_K=\sum _i{𝒲}_{A\to B}({𝐅}_i)=\sum {𝒲}_{A\to B}({𝐅}^c)+\sum {𝒲}_{A\to B}({𝐅}^{nc})$, soit$\text{d}{ℰ}_c=\sum \delta W({𝐅}^c)+\sum \delta W({𝐅}^{nc})$. En soustrayant de chaque côté par $\sum \delta W({𝐅}^c)=-\text{d}{ℰ}_{𝓅}$, on obtient l'énoncé du théorème de l'énergie mécanique$$\mathrm{\Delta }{ℰ}_m=\sum {𝒲}_{A\to B}({𝐅}^{nc})$$À partir de là, on peut énoncer un résultat de conservation de l'énergie : Tout sytème soumis uniquement à des forces conservatives voit son énergie mécanique se conserver.

Théorème de la puissance mécanique

Considérons un point matériel $M$ de masse $m$ constante soumis à $\sum _i{𝐅}_i$ (dont certaines sont conservatives) et évoluant à une vitesse $𝐯$ dans un référentiel galiléen $ℛ$.

On note $\sum _i{𝐅}_i=\sum {𝐅}^c+\sum {𝐅}^{nc}$ où ${𝐅}^c$ désigne une force conservative et ${𝐅}^{nc}$ une force non conservative.

On peut appliquer le théorème de l'énergie mécanique, qui donne $\mathrm{\Delta }{ℰ}_m=\sum {𝒲}_{A\to B}({𝐅}^{nc})$ soit sous forme infinitésimale $\text{d}{ℰ}_m=\sum \delta W({𝐅}^{nc})$, ce qui en divisant de chaque côté par $\text{d}t$ donne l'énoncé du théorème de la puissance mécanique.

$$\frac{\text{d}{ℰ}_m}{\text{d}t}=\sum 𝒫({𝐅}^{nc})$$

Applications de ces théorèmes

Calculs de travaux et d'énergie potentielle

Travail d'une force constante, cas particulier du poids

Si la force est constante, alors ${𝒲}_{A\to B}=\underset{A}{\overset{B}{\int }}𝐅\text{d}𝐎𝐌=𝐅\underset{A}{\overset{B}{\int }}\text{d}𝐎𝐌=𝐅.[𝐎𝐁-𝐎𝐀]=𝐅.𝐀𝐁$

Dans le cas du poids, on a donc ${𝒲}_{A\to B}=-mg{𝐞}_z.((x_B-x_A){𝐞}_x+(y_B-y_A){𝐞}_y+(z_B-z_A){𝐞}_z)=-mg(z_B-z_A)$

Travail d'une force de frottements linéaire

On a alors ${𝒲}_{A\to B}=\underset{A}{\overset{B}{\int }}𝐅\text{d}𝐎𝐌=\underset{A}{\overset{B}{\int }}-\alpha 𝐯\text{d}𝐎𝐌=\underset{A}{\overset{B}{\int }}-\alpha v^2\text{d}t=-\underset{A}{\overset{B}{\int }}\alpha v^2\text{d}t$ et on en conclut donc que le travail de la force de frottements est toujours résistif (la démonstration serait analogue pour des frottements quadratiques)

Cas d'une force orthogonale

Considérons une force orthogonale au mouvement (au moins pendant un instant infinitésimale), ce qui signifie que $\delta W=𝐅.\text{d}𝐎𝐌=0$.

On dit dans ce cas que la force ne travaille pas. Elle ne fournit ni ne retire de l'énergie à un système.

Calcul de l'énergie potentielle gravitationnelle et de l'énergie potentielle électrostatique

On a ${𝐅}_{grav}=-𝒢\frac{m{m}^{\prime }}{r^2}{𝐞}_r$. Cette force est conservative (elle ne dépend que de la position). On calcule donc

$\text{d}{ℰ}_{pgrav}=-\delta W=-𝐅\text{d}𝐎𝐌=-𝒢\frac{m{m}^{\prime }}{r^2}{𝐞}_r\text{d}r{𝐞}_r=-𝒢\frac{m{m}^{\prime }}{r^2}\text{d}r$ soit $\frac{\text{d}{ℰ}_p}{\text{d}r}=-𝒢\frac{m{m}^{\prime }}{r^2}$ soit ${ℰ}_{pgrav}(r)=𝒢\frac{m{m}^{\prime }}{r}+cste$. On pose en général $cste=0$

Concernant la force électrostatique, on a ${𝐅}_{elec}=\frac{q{q}^{\prime }}{4\pi {\epsilon }_0{r}^2}{𝐞}_r$. L'expression de la force électrostatique est analogue à l'expression de la force gravitationnelle (une constante multipliée par le produit des grandeurs caractéristiques (la masse ou la charge) et divisé par la distance au carré, le tout porté par un vecteur radial). Aussi les calculs sont-ils analogues également. On peut mener exactement les mêmes calculs et on trouve ${ℰ}_{pelec}(r)=\frac{q{q}^{\prime }}{4\pi {\epsilon }_{0}r}+cste$ et on pose en général $cste=0$

Calcul de l'énergie potentielle de pesanteur

On a $𝐏=m𝐠$. Cette force est conservative (elle est même constante). On calcule donc

$\text{d}{ℰ}_{pp}=-\delta W=-𝐅\text{d}𝐎𝐌=-m𝐠(\text{d}x{𝐞}_x+\text{d}y{𝐞}_y+\text{d}z{𝐞}_z)=-m\text{d}z𝐠.{𝐞}_z=mg\text{d}z$, soit $\frac{\text{d}{ℰ}_{pp}}{\text{d}z}=mg$, soit ${ℰ}_{pp}=mgz+cste$ et on pose en général $cste=0$

Calcul de l'énergie potentielle élastique

On a ${𝐅}_{elastique}=-kx{𝐞}_x$. Cette force est conservative (elle ne dépend que de la position). On calcule donc $\text{d}{ℰ}_{pelastique}=-\delta W=-𝐅.\text{d}𝐎𝐌=kx{𝐞}_x\text{d}x{𝐞}_x=kx\text{d}x$ et on trouve donc $kx=\frac{\text{d}{ℰ}_p}{\text{d}x}$, soit ${ℰ}_p=\frac{1}{2}k{x}^2+cste$. On pose en général $cste=0$

Calculs des positions d'équilibre, notion de stabilité ou d'instabilité d'un équilibre

Considérons un système soumis uniquement à des forces conservatives. La première loi de Newton nous donne une condition nécessaire et suffisante d'équilibre, à savoir $\sum 𝐅=\mathrm{𝟎}$. On obtient alors une nouvelle condition d'équilibre, à savoir $𝐠𝐫𝐚𝐝({ℰ}_p)=\mathrm{𝟎}$. De plus, dans le cas particulier où la force (et donc l'énergie potentielle) ne dépend que d'un seul paramètre de longueur $x$, cette condition devient alors : Il y a équilibre en $x_0$ si ${\left(\frac{\text{d}{ℰ}_p}{\text{d}x}\right)}_{x_0}=0$. Dans le cas particulier où la force (et donc l'énergie potentielle) ne dépend que d'un seul paramètre angulaire $\theta$, cette condition devient alors : Il y a équilibre en ${\theta }_0$ si ${\left(\frac{1}{r}\frac{\text{d}{ℰ}_{𝓅}}{\text{d}\theta }\right)}_{{\theta }_0}=0$, soit $\left(\frac{\text{d}{ℰ}_p}{\text{d}\theta }\right)=0$

L'étude énergétique nous permet également de discuter de la nature stable ou instable d'un équilibre. Soit une position d'équilibre, et soit un point $M$ placé en cette position d'équilibre. L'équilibre est dit stable si, lorsque l'on éloigne le point $M$ de cette position, il a naturellement tendance à retrouver cette position d'équilibre (par exemple, une bille posée dans un bol est en équilibre stable quand elle est au fond du bol). L'équilibre est dit instable si, lorsque l'on éloigne le point $M$ de cette position, il ne retrouve pas cette position (par exemple, une bille posée tout en haut d'une haut d'une colline est en équilibre instable, si on l'éloigne du sommet elle dévalera la co lline et ne retrouvera pas le sommet).

Courbe d'énergie potentielle

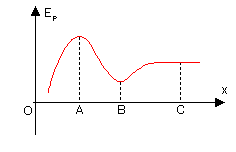
La stabilité ou l'instabilité d'un équilibre se situe de la courbe d'énergie potentielle (voir figure ci-contre). Si, en une position d'équilibre (ie en un maximum ou un minimum d'énergie potentielle), la courbe est convexe (c'est-à-dire au-dessus de sa tangente), alors la position est stable (position B sur la figure ci-contre). Si en une position d'équilibre la courbe est concave (c'est-à-dire au-dessous de sa tangente), alors la position est instable (position A sur la figure ci-contre).

Mathématiquement, soit $x_0$ une position d'équilibre. Cet équilibre est stable si, et seulement si, ${\left(\frac{{\text{d}}^2{ℰ}_p}{\text{d}{x}^2}\right)}_{x_0}\ge 0$

Il est instable si ${\left(\frac{{\text{d}}^2{ℰ}_p}{\text{d}{x}^2}\right)}_{x_0}<0$

(Le résultat serait analogue pour une variable angulaire)

Application du théorème de l'énergie cinétique

On rappelle l'énoncé du théorème de l'énergie cinétique

$$\mathrm{\Delta }{ℰ}_K=\sum _i{𝒲}_{A\to B}({𝐅}_i)$$

Partons d'un exemple : considérons un objet en chute libre sans vitesse initiale et ne subissant pas de frottements. On sait donc qu'à $t=0$, $z=0$ et $v=0$. On cherche à déterminer quelle est la vitesse de l'objet quand il atteint une position $z_0$.

Ce problème est parfaitement résoluble en utilisant le principe fondamental de la dynamique, en procédant comme suit : on commence par déterminer l'équation différentielle du mouvement, puis on obtient l'équation paramétrique du mouvement, et on résout une équation du type $f(t)=z_0$. Cependant, le théorème de l'énergie cinétique va nous permettre de résoudre plus rapidement ce problème. De façon générale, le théorème de l'énergie cinétique doit être utilisé quand on cherche à déterminer une vitesse connaissant une autre vitesse et une position, ou une position connaissant une autre position et une vitesse.

Appliquons le théorème de l'énergie cinétique dans le cas de notre problème. Pour simplifier, notons $A$ l'instant initial et $B$ l'instant. On a alors

$\mathrm{\Delta }{ℰ}_k=\frac{1}{2}m{v}_B^2-\frac{1}{2}m{v}_A^2=\sum _i{𝒲}_{A\to B}({𝐅}_{𝐢})={𝒲}_{A\to B}(𝐏)=-mg(z_B-z_A)$

Or, à l'instant $A$, $v_A=0$ et $z_A=0$. De plus, à l'instant $B$, $z_B=z_0$. Il vient donc $\frac{1}{2}m{v}_B^2=mg{z}_B$ et ainsi $$v_B=\sqrt{2g{z}_B}$$

Application du théorème de la puissance cinétique

La deuxième loi de Newton est une relation vectorielle. On obtient donc, en l'utilisant, trois relations. L'une d'entre elle nous permet d'obtenir l'équation différentielle du mouvement, et les deux autres sont, ou bien inutiles, ou bien intéressantes pour déterminer des forces inconnues (force de tension d'un fil, de réaction, etc). Cependant, cette démarche peut être lourde, notamment dans des cas où il faut effectuer des projections lourdes et fastidieuses.

Le théorème de la puissance cinétique, quant à lui, est un théorème scalaire. Il est donc particulièrement intéressant quand on s'intéresse à un problème à un degré de liberté. Pour illustre cela, reprenons l'exemple du pendule simple. On se place dans le référentiel du laboratoire supposé galiléen, et en coordonnées polaires. Le système est soumis à la force de tension du fil et au poids. Appliquons le théorème de la puissance cinétique.

$$\frac{\text{d}{ℰ}_K}{\text{d}t}=𝒫(𝐏)+𝒫(𝐓)$$Déterminons ensuite ${ℰ}_K$. On a ${ℰ}_K=\frac{1}{2}m{v}^2$. Nous sommes en coordonnées polaires, donc $𝐎𝐌(t)=L{𝐞}_r$ où $L$ est la longueur du fil (qui est une constante car le fil est supposé absolument indéformable). Ainsi, $𝐯(t)=L\dot{\theta }{𝐞}_{\theta }$ et donc $v^2=L^2{\dot{\theta }}^2$. Ainsi, ${ℰ}_K=\frac{1}{2}m{L}^2{\dot{\theta }}^2$.

Il vient donc, par simple calcul de dérivation, que $\frac{\text{d}{ℰ}_K}{\text{d}t}=\frac{\text{d}}{\text{d}t}\left(\frac{1}{2}m{L}^2{\dot{\theta }}^2\right)=m{L}^2\dot{\theta }\ddot{\theta }$

Calculons maintenant les puissances du poids et de la force de tension.

Concernant la force de tension, on a $𝐓=-T{𝐞}_r$ et $𝐯=L\dot{\theta }{𝐞}_{\theta }$. Or, ${𝐞}_r$ et ${𝐞}_{\theta }$ étant orthogonaux, $𝒫(𝐓)=𝐓.𝐯=0$

Pour ce qui est du poids, on a $𝐏=mg\cos \theta {𝐞}_r-mg\sin \theta {𝐞}_{\theta }$ et $𝐯=L\dot{\theta }{𝐞}_{\theta }$. Ainsi, $𝒫(𝐏)=-mLg\sin \theta \dot{\theta }$

L'application du théorème de l'énergie cinétique donne donc

$$m{L}^2\dot{\theta }\ddot{\theta }=-mLg\sin \theta \dot{\theta }$$

soit

$$\ddot{\theta }+\frac{g}{L}\sin \theta =0$$On retrouve ainsi l'équation différentielle du mouvement du pendule simple obtenue avant grâce à la deuxième loi de Newton.

Application du théorème de l'énergie mécanique

Le théorème de l'énergie mécanique s'utilise comme le théorème de l'énergie cinétique, et permet de répondre aux mêmes questions.

Application du théorème de la puissance mécanique

Le théorème de la puissance mécanique s'utilise comme le théorème de la puissance cinétique, et permet de répondre aux mêmes questions. Modèle:Bas de page