Initiation à l'élasticité/Forces et contraintes

Force

Vocabulaire

Dans la littérature, on retrouvera différents termes désignant la force, par exemple la sollicitation, l’effort ou éventuellement l’actions mécaniques. Dans cette leçon, nous parlerons de force.

M centré sur un élément dS

M centré sur un élément dV

On distingue deux types de forces :

1. Les actions mécaniques ou efforts de contact qui s’exercent sur une surface : Forces de Surface.
2. Les actions mécaniques ou efforts à distance qui s’exerce sur un volume : Forces de Volume.

La représentation mathématique d'une force se fait par un vecteur qui s'applique au point M.

M est centré au choix sur :

• un élément dS (Force de Surface),
• un élément dV (Force de Volume).

$||\overrightarrow{F}||$ : la norme représente la valeur de la force en Newton. Pour connaitre la dimension d'une force on effectue: $[F]=\frac{[M]*[L]}{[T{]}^2}\Rightarrow kg.m.s^{-2}$

Ensembles de force

Parmi les efforts de surface il y a les efforts de cohésion qui représentent les efforts générés par la matière pour rester cohérente. Si les efforts dans la pièce mécanique dépassent les efforts de cohésion limites, la pièce casse.

Un champ de vecteur : ensemble de vecteur défini sur un volume de l'espace

Exemple: On entendra par champ de force, l’ensemble des forces sur une surface $\overrightarrow{F}$ (x,y,z) (autre exemple : le champ de vitesse,...)

Densité de forces : force linéique appliqué sur une poutre

on décrit une force par l'intermédiaire d'une densité

F/longueur

F/surface "densité de force" → même dimension qu'une contrainte

F/volume

Soit un volume de surface S de volume n de normal $\overrightarrow{n}$ Sur cet objet sont appliquées des forces (de surface, de volume). Ces forces là qui sont appliquées sur la surface extérieur de l’objet sont appelée densité de force si nécessaire.

Les forces de cohésion ne sont pas décrites par des densités de force mais par des contraintes.

Torseur des efforts :

Résultante d'un champ de force en un point:
$\left\{\begin{array}{c}\overrightarrow{R}\\ \overrightarrow{M}\end{array}\right\}$_A
Torseur de $\overrightarrow{R}$ en A

Résultante de force

La force de résultante (force ponctuelle) est toujours la résultante d’un ensemble de forces de surface.

Vecteurs Contraintes

Définition

La notion de vecteur contrainte est plutôt relié aux forces de cohésion. On se place à l’intérieur d’un volume de matière.

Soit M un point de V autour duquel on définit ΔS surface de ΔV

Sur ΔS existe un champ de force de cohésion Δ$\overrightarrow{F}$ (ce n’est pas une densité de force) Δ$\overrightarrow{F}$ s’exerce sur cette surface la qui passe par M, on définit ΔS par $\overrightarrow{n}$ la normal en M.

$\overrightarrow{F}(M,\overrightarrow{n})$= Force qui s’exerce au point M sur la surface de normal $\overrightarrow{n}$ Principe de la mécanique classique :

$\{\begin{array}{c}\underset{\mathrm{\Delta }S\to 0}{\lim }\frac{\overrightarrow{F}(M,\overrightarrow{n})}{\mathrm{\Delta }S}=\overrightarrow{C}(M,\overrightarrow{n})\\ li{m}_{\mathrm{\Delta }S\to 0}\frac{\overrightarrow{M_{\frac{\overrightarrow{F}}{M}}}}{\mathrm{\Delta }S}=\overrightarrow{0}\end{array}$ $\overrightarrow{C}$ est le vecteur contrainte qui s’exerce en M sur la surface de normal $\overrightarrow{n}$

Modèle:Définition On définit alors le vecteur contrainte comme ceci: $\underset{\mathrm{\Delta }S\to 0}{\lim }\frac{\overrightarrow{F}}{\mathrm{\Delta }S}=\overrightarrow{C}(M,\overrightarrow{n})$

Cette définition est une définition théorique, en pratique on détermine $\overrightarrow{C}$ par d'autres moyens, notamment avec les équations de la mécanique et on utilise l'équation précédente pour trouver $\overrightarrow{F}$ :

$\overrightarrow{F}=\underset{s}{\int }\overrightarrow{C}(M,\overrightarrow{n}).\mathrm{d}S$ $\overrightarrow{F}$ est une force extérieure au système et donc $\overrightarrow{C}$ est la contrainte extérieure qui est appliquée sur la surface considérée. On définit un champ de contraintes $\overrightarrow{C}(M,\overrightarrow{n})$, c’est l’ensemble des vecteurs contraintes définis sur V, le volume.

Représentation et décomposition

La représentation de $\overrightarrow{C}(M,\overrightarrow{n})$

• $\overrightarrow{C}(M,\overrightarrow{n})$ dépend au total de 5 paramètres :

3 paramètres pour les coordonnées du point M

2 paramètres pour la surface (coordonnées de $\overrightarrow{n}$

• Expression de la dimension de la contrainte : $[\overrightarrow{C}]=\frac{[F]}{[S]}=\frac{[M].[L]}{[T{]}^2.[L{]}^2}=\frac{[M]}{[T{]}^2.[L]}$
• L'unité de la contrainte est le Pascal. $1Pa=1N.m^{-2}$
• L'ordre de grandeur de la contrainte dans un métal est le MPa.

La décomposition de $\overrightarrow{C}(M,\overrightarrow{n})$

Lien entre l'outil mathématique et la réalité. On définit un repère local à partir de $\overrightarrow{n}$.

On va exprimer $\overrightarrow{C}(M)$ par rapport à $\overrightarrow{n}$ en M. La décomposition de $\overrightarrow{C}$ se fait sur ce repère. On écrit :

$\begin{array}{ccc}\overrightarrow{C}& =& \sigma .\overrightarrow{n}+\overrightarrow{\tau }\\ & =& \overrightarrow{\sigma }+\overrightarrow{\tau }\end{array}$

Avec $\sigma$ : contrainte normale.
​ $\tau$ : contrainte tangentielle de cisaillement. Méthode pour calculer $\sigma$ et $\tau$ :

$\{\begin{array}{c}\sigma =\overrightarrow{C}.\overrightarrow{n}\\ \overrightarrow{\tau }=\overrightarrow{C}-\sigma .\overrightarrow{n}\end{array}$ Dans certains ouvrages on définit $\overrightarrow{t}$, un vecteur tangent unitaire

$\overrightarrow{C}=\sigma .\overrightarrow{n}+\tau .\overrightarrow{t}$

• Conditions pour définir $\overrightarrow{t}$ :

$\overrightarrow{a}$ pour définir la direction

sens $(\overrightarrow{n},\overrightarrow{t})$ repère direct

$||\overrightarrow{t}||=1$

On définit cette décomposition par intérêt pratique et physique mais aussi pour introduire les notions de pression et de cisaillement. $\{\begin{array}{c}\sigma >0=\text{traction}\\ \sigma <0=\text{compression}\end{array}$ On observe en pratique que les materiaux sont plus sensibles au cisaillement.

Pression

La Pression P_Ambiante est supérieure à 0 et elle génère un vecteur contrainte toujours normal à la surface S et dirigée vers S.
​

Avec $\overrightarrow{n}$ le vecteur normal à S, on écrit alors pour un objet uniquement soumis à la pression :

$\overrightarrow{C}=-p.\overrightarrow{n}$

Tenseur des contraintes

Motivation

Pour comprendre les problèmes posés par la représentation des contraintes on doit déterminer quelle est la surface à prendre en compte lorsque l’on considère:
​

$\overrightarrow{C}=\frac{\overrightarrow{F}}{S}$

Soit une plaque:

​

Quelle est la contrainte appliquée en M ? Première approche :

On choisit $S_1$

$\overrightarrow{C}=\frac{\overrightarrow{T}}{S_1}\Rightarrow$ appliquée sur $S_1$

On définit une surface qui passe en M grâce à son vecteur normal $\overrightarrow{n}$ en M:

​

On choisit un repère centré en M, orthonormé cartésien choisi en fonction de la géométrie de la pièce et des sollicitations. Soit $\alpha =\widehat{\overrightarrow{x}\overrightarrow{n}}$ avec $||\overrightarrow{n}||=1$

$\overrightarrow{x}=\{\begin{array}{c}nx=\cos \alpha \\ ny=\sin \alpha \end{array}$ S la section (surface) est définie par M et $\overrightarrow{n}$. Pour déterminer quel est le vecteur contrainte en M sur S il faut déterminer la force appliquée par l'extérieur sur S.

Par équilibre, sur S l'effort est : $\overrightarrow{T}$ réparti sur S; et la résultante de $\overrightarrow{T}$ est opposée à la résultante de $\overrightarrow{-T}$

La force appliquée en $M$ $\{\begin{array}{c}-T^R=T_x\\ 0\end{array}$ d'où $\overrightarrow{C}={\overrightarrow{T}}_x^M$ Soit $e$ l'épaisseur et $h$ la hauteur on a :
​

$S=\frac{e*h}{cos\alpha }$

et

$\overrightarrow{C}=\frac{{\overrightarrow{T}}_x^M}{e*h}*cos\alpha$ $\overrightarrow{C}$ varie suivant la surface choisie Lorsque l’on parle d'un vecteur contrainte en un point M il faut préciser la surface sur laquelle il est appliqué:

• On souhaite définir un outil mathématique qui permet de décrire la contrainte en M sans avoir à préciser la surface.
• Comment définir mathématiquement un vecteur $\overrightarrow{C}$ en M avec une définition cohérente de la surface S ?

Définition du tenseur des contraintes

Le tenseur des contraintes est par définition un outil mathématique qui permet de définir complètement l'état de contrainte en un point M.

Attention aux notations :

Le tenseur des contraintes est généralement noté $\tilde{\sigma }$
​ Il ne faut pas confondre :

• $\sigma$ la contrainte normale
• $\tilde{\sigma }$ le tenseur des contraintes
• $(\overrightarrow{\sigma })=\overrightarrow{C}$ le vecteur contrainte

$\tilde{\sigma }$ est représenté par une matrice carrée 3x3 (espace 3D) dans un repère donné.
​

$\tilde{\sigma }=\left(\begin{array}{ccc}.& .& .\\ .& .& .\\ .& .& .\end{array}\right)$ _{(O,$\overrightarrow{x}$,$\overrightarrow{y}$,$\overrightarrow{z}$)}
​

Définition implicite du tenseur des contraintes $\tilde{\sigma }$ :
​

$\overrightarrow{C}(M;\overrightarrow{n})=\tilde{\sigma }(M)\overrightarrow{n}$

Intérêt du tenseur des contraintes

Considérons la relation $\overrightarrow{C}=\tilde{\sigma }\overrightarrow{n}$ dans le cas d'une poutre en traction simple :

Soit le tenseur $\tilde{\sigma }$ donné : $\tilde{\sigma }=\left(\begin{array}{ccc}T/S& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$ _{(O,$\overrightarrow{x}$,$\overrightarrow{y}$,$\overrightarrow{z}$)}
​ L'effort $\overrightarrow{T}$ est appliqué sur la poutre selon l'axe $\overrightarrow{x}$
​ Soit le vecteur normal : $\overrightarrow{n}\left|\begin{array}{c}1\\ 0\\ 0\end{array}\right|$ Soit le vecteur contrainte : $\overrightarrow{C}\left|\begin{array}{c}T/S\\ 0\\ 0\end{array}\right|$ Expression de la contrainte normal $\sigma$ sur $\overrightarrow{n}$

$\sigma =\overrightarrow{C}.\overrightarrow{n}=\left|\begin{array}{c}T/S\\ 0\\ 0\end{array}\right|.\left|\begin{array}{c}1\\ 0\\ 0\end{array}\right|=T/S$ $\sigma =T/S$

Contraintes principales, directions principales et invariants du tenseur des contraintes

On part d'un $\tilde{\sigma }$ défini en un point M, en 3 dimensions. On suppose que $\tilde{\sigma }$ est symétrique.
​ La matrice qui représente $\tilde{\sigma }$ admet alors 3 valeurs propres et 3 vecteurs propres.

• Les valeurs propres définissent les contraintes principales
• Les vecteurs propres définissent les directions principales

Convention de notation: ${\sigma }^I,{\sigma }^{II},{\sigma }^{III}$ où ${\sigma }^I$ est la plus grande. Modèle:Définition

Remarque: Dans les directions principales

• le tenseur est diagonal,
• Sur les faces normales aux directions principales : $\overrightarrow{\tau }=\overrightarrow{0}$

Remarque: On définit les invariants de $\tilde{\sigma }$ :

Valeurs propres en 2 dimensions : ${\lambda }^2+J^I\lambda +J^{II}=0$

Valeurs propres en 3 dimensions: ${\lambda }^3+J^{II}{\lambda }^2+J^{III}=0$

Tous les repères dans lesquels $\tilde{\sigma }$ sera exprimé, $J^I,J^{II}et{J}^{III}$ sont toujours les mêmes (mêmes valeurs).

Interprétations et représentations du tenseur des contraintes

Interprétation des représentations du tenseur des contraintes dans différents repères

Le tenseur des contraintes $\tilde{\sigma }$ représente l’état de contrainte en M.

Intérêt du choix d’un repère : le choix du repère doit être fait intelligemment car il permet de simplifier les calculs. Le même tenseur $\tilde{\sigma }$ et peut en effet être représenté par des matrices dans différents repères :

$\tilde{\sigma }=\left(\begin{array}{ccc}.& .& .\\ .& .& .\\ .& .& .\end{array}\right)$ _{(O,$\overrightarrow{x}$,$\overrightarrow{y}$,$\overrightarrow{z}$)}

$\tilde{\sigma }=\left(\begin{array}{ccc}.& .& .\\ .& .& .\\ .& .& .\end{array}\right)$ _{(O,${\overrightarrow{x}}^{\prime }$,${\overrightarrow{y}}^{\prime }$,${\overrightarrow{z}}^{\prime }$)}

$\tilde{\sigma }=\left(\begin{array}{ccc}{\sigma }_1& 0& 0\\ 0& {\sigma }_2& 0\\ 0& 0& {\sigma }_3\end{array}\right)$ _{(eModèle:Exp,eModèle:Exp,eModèle:Exp)}

Interprétation des termes du tenseur des contraintes dans différents repères

Dans tout repère 2D :
​

$\tilde{\sigma }(M)=\left(\begin{array}{cc}\sigma xx& \sigma xy\\ \sigma xy& \sigma yy\end{array}\right)$_{(O,$\overrightarrow{x}$,$\overrightarrow{y}$)}

Selon la notation classique :
​

$\sigma$xy
​

x représente le nombre de ligne
​

y représente le nombre de colonne
​

Remarque : Le tenseur des contraintes est symétrique donc $\sigma$xy=$\sigma$yx On calcul $\overrightarrow{C}$,$\sigma$,$\overrightarrow{\tau }$ pour différentes forces : ($\overrightarrow{x}$) ; $\overrightarrow{n}\left|\begin{array}{c}1\\ 0\end{array}\right|$ ; $\overrightarrow{C}\left|\begin{array}{c}\sigma xx\\ \sigma xy\end{array}\right|$ ; $\sigma$=$\sigma$xx ; $\overrightarrow{\tau }=\left|\begin{array}{c}\sigma xx\\ \sigma xy\end{array}\right|-\left|\begin{array}{c}\sigma xx\\ 0\end{array}\right|=\left|\begin{array}{c}0\\ \sigma xy\end{array}\right|$

($\overrightarrow{y}$) ; $\overrightarrow{n}\left|\begin{array}{c}0\\ 1\end{array}\right|$ ; $\overrightarrow{C}\left|\begin{array}{c}\sigma xy\\ \sigma yy\end{array}\right|$ ; $\sigma$=$\sigma$yy ; $\overrightarrow{\tau }=\left|\begin{array}{c}\sigma xy\\ 0\end{array}\right|$ Les termes diagonaux de $\tilde{\sigma }$ correspondent aux contraintes normales sur les forces qui ont pour vecteur normal, les vecteurs de base du repère choisi pour exprimer $\tilde{\sigma }$.

Les termes non diagonaux de$\tilde{\sigma }$ correspondent aux contraintes tangentielles sur les mêmes forces. Dans le repère principal :

$\tilde{\sigma }=\left(\begin{array}{ccc}{\sigma }_1& 0& 0\\ 0& {\sigma }_2& 0\\ 0& 0& {\sigma }_3\end{array}\right)$ _{(eModèle:Exp,eModèle:Exp,eModèle:Exp)} Les contraintes principales correspondent aux contraintes normales sur les forces qui ont pour normal les directions principales.

Les contraintes tangentielles sont nulles sur les forces qui ont pour normal les directions principales.

Si $\overrightarrow{\tau }=0$ sur une face, alors le vecteur normal à cette force est direction principale. Force libre → $\overrightarrow{\tau }=0$

→ normal à la force de direction principale.

Même raisonnement si les efforts appliqués sont perpendiculaires à la face.

« Force libre » : aucune sollicitation extérieure appliquée sur cette face $\tilde{\sigma }(x,y,z)$ On a définit $\tilde{\sigma }$

C’est un champ de contraintes : il est défini en chaque point M d’une pièce et a priori différent en chaque point.

On a défini :

• contrainte principale (valeur propre)
• direction principale
• la signification des termes

Décomposition du tenseur des contraintes

Parfois on décompose :
​

$\tilde{\sigma }=-p\tilde{I}+\tilde{\tau }$
​

→ plutôt en mécanique des fluides ou en plasticité
​

Mathématiquement on définit la partie sphérique et la partie déviatrice de $\tilde{\sigma }$

Partie sphérique de $\tilde{\sigma }$

Par définition la pression ambiante de l'air dans/sur un matériau est : $p=-\frac{tr(\tilde{\sigma })}{3}$

${\tilde{\sigma }}^S=\frac{tr(\tilde{\sigma })}{3}.\tilde{I}$

avec $\tilde{I}=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$ le tenseur de contrainte associé à une sollicitation par pression ambiante p dans toutes les directions et sur toutes les faces.

On est dans un état hydrostatique on a le tenseur de contrainte suivant:

$\tilde{\sigma }=\left(\begin{array}{ccc}-p& 0& 0\\ 0& -p& 0\\ 0& 0& -p\end{array}\right)$

$Trace({\tilde{\sigma }}^I)=-3p$

et

$p=-\frac{tr(\tilde{\sigma })}{3}$ où 3 est la moyenne des termes de la diagonale.

$\tilde{\sigma }=\left(\begin{array}{ccc}3& 2& 1\\ -2& 2& 0\\ 1& 0& 4\end{array}\right)\Rightarrow tr(\tilde{\sigma })=9\Rightarrow {\tilde{\sigma }}^S=\left(\begin{array}{ccc}3& 0& 0\\ 0& 3& 0\\ 0& 0& 3\end{array}\right)$

${\tilde{\sigma }}^S$ représente la sollicitation en pression toujours perpendiculaire à la surface.

$P=-3$

Dans les cas des fluides $P>0$

Partie déviatrice ou déviateur de $\tilde{\sigma }$

${\tilde{\sigma }}^D=\tilde{D}=\tilde{S}$ et Modèle:Coloré $\left(\begin{array}{ccc}3& 2& 1\\ -2& 2& 0\\ 1& 0& 4\end{array}\right)-\left(\begin{array}{ccc}3& 0& 0\\ 0& 3& 0\\ 0& 0& 3\end{array}\right)=\left(\begin{array}{ccc}0& 2& 1\\ -2& -1& 0\\ 1& 0& 1\end{array}\right)$ $\left(\begin{array}{ccc}3& .& .\\ .& 3& .\\ .& .& 3\end{array}\right)$ : parallèle.

$\left(\begin{array}{ccc}0& .& .\\ .& -1& .\\ .& .& 1\end{array}\right)$ représente les sollicitations tangentes. Utilité :

• description des fluides,
• plasticité,
• critères de résistance.

La partie déviatrice est la partie la plus dangereuse.

États de contraintes particuliers

On choisit des sollicitations simples et on détermine $\tilde{\sigma }$

État de traction simple

$\tilde{\sigma }=\left(\begin{array}{ccc}\frac{T}{S}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$ On veut déterminer $\tilde{\sigma }(M)$ le tenseur des contraintes en tout point M de la barre. Le vecteur appliqué par l'extérieur sur la face normale $\overrightarrow{i}=\left|\begin{array}{c}1\\ 0\\ 0\end{array}\right|$.

C'est le vecteur $\overrightarrow{C}=\left|\begin{array}{c}\frac{T}{S}\\ 0\\ 0\end{array}\right|$ . Ceci est vrai pour toute surface S' parallèle à $S^x$, par équilibre.

Sur les surfaces $S^y$ et $S^z$ rien n'est appliqué et on a $\overrightarrow{C}=0$

On est dans un état de compression / traction simple.

Un seul des éléments diagonaux de $\tilde{\sigma }$ est non nul. $\left(\begin{array}{ccc}\alpha & 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),\left(\begin{array}{ccc}0& 0& 0\\ 0& \alpha & 0\\ 0& 0& 0\end{array}\right),\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& \alpha \end{array}\right)$

États de cisaillement pur

La plaque est obligatoirement carrée pour des raisons d'équilibre des résultantes des forces.

• $\overrightarrow{C}$ en $S^x:\overrightarrow{C}=\left|\begin{array}{c}0\\ -\tau \\ 0\end{array}\right|$

et

• $\overrightarrow{C}$ en $S^y=\left|\begin{array}{c}-\tau \\ 0\\ 0\end{array}\right|$

on a donc : $\tilde{\sigma }=\left(\begin{array}{ccc}0& -\tau & 0\\ -\tau & 0& 0\\ 0& 0& 0\end{array}\right)$

État plan de contraintes

On passe de 3 dimensions à 2 dimensions.

On prend en exemple un plan en traction / cisaillement. Les sollicitations sont toutes dans le même plan $(0,\overrightarrow{x},\overrightarrow{y})$ $\tilde{\sigma }=\left(\begin{array}{ccc}{\sigma }^T& \tau & 0\\ \tau & -{\sigma }^P& 0\\ 0& 0& 0\end{array}\right)$

• Remarque:

$\left(\begin{array}{ccc}.& .& 0\\ .& .& 0\\ 0& 0& 0\end{array}\right)$ cette forme de matrice est caractéristique de l'état de plan de contraintes.

Cercle de Mohr

voir lien ci-dessous pour plus d'information :

Introduction à l'élasticité/Contraintes#Représentation de Mohr

Ellipsoïde de Lamé

Ellipsoïde de Lamé : représentation graphique de l’ensemble des vecteurs contraintes $\overrightarrow{C}$ associés à un tenseur des contraintes, $\tilde{\sigma }$ en un point d'un volume. Dans tous les cas on se place dans le repère principal en 3 dimensions.

$\tilde{\sigma }=\left(\begin{array}{cc}{\sigma }^I& 0\\ 0& {\sigma }^{II}\end{array}\right)$ ; $\overrightarrow{C}$ sur une face de normale $\overrightarrow{n}=\left|\begin{array}{c}{n}_x\\ n_y\end{array}\right|$ or $\begin{array}{ccc}\overrightarrow{C}& =& \tilde{\sigma }.\overrightarrow{n}\\ & =& \left(\begin{array}{cc}{\sigma }^I& 0\\ 0& {\sigma }^{II}\end{array}\right)\left(\begin{array}{c}{n}_x\\ n_y\end{array}\right)=\left|\begin{array}{c}{\sigma }^I.n_x\\ {\sigma }^{II}.n_y\end{array}\right|\end{array}$ Dans le repère principal.

Représentation graphique et physique de $\overrightarrow{C}$ à partir de $\tilde{\sigma }$

Par définition $||\overrightarrow{n}||=1\Rightarrow {n_x}^2+{n_y}^2=1(*)$ $\overrightarrow{C}=\begin{array}{c}{C}_x={\sigma }^I.n_x\\ C_y={\sigma }^{II}{n}_y\end{array}\Rightarrow \begin{array}{c}{n}_x=\frac{C_x}{{\sigma }^I}\\ n_y=\frac{C_y}{{\sigma }^{II}}\end{array}$ On injecte ça dans (*) : $\frac{{C_x}^2}{{{\sigma }^I}^2}+\frac{{C_y}^2}{{{\sigma }^{II}}^2}=1$ $C_x={\sigma }^I\Rightarrow {\frac{{\sigma }^I}{{\sigma }^I}}^2+{\frac{C_y}{{\sigma }^{II}}}^2=1$ $\Rightarrow C_y=0$ $\overrightarrow{C}=\left|\begin{array}{c}{\sigma }^I\\ 0\end{array}\right|.\overrightarrow{n}\left|\begin{array}{c}1\\ 0\end{array}\right|$

Définition des conditions limites sur les contraintes

Il faut connaitre les sollicitations appliquées sur le volume considéré (sollicitations définies par des efforts ou des vecteurs contraintes). Modèle:Coloré

• Exemple:

La forme du volume influence $\tilde{\sigma }$.

Il faut définir la forme du volume pour définir les contraintes limites. Il faut donc définir les équations des surfaces extérieures au volume.

Remarque: Les forces de volume n'interviennent pas dans les conditions limites (par exemple le poids).

Exemples

L'objectif de cet exemple est d'écrire les contraintes limites sur la digue.

1. Faire le bilan des actions mécaniques connues:

• pression de l'eau :

• Poids : $\overrightarrow{P}$
• Réaction du sol.
• Pression atmosphérique : toujours négligée car très inférieure aux contraintes mises en jeu.

1. Écrire les contraintes limites:

On doit faire cette démarche pour toutes les faces du systèmes.

• Face 1: équation : $x=0$
  • $\overrightarrow{n}\left|\begin{array}{c}-1\\ 0\end{array}\right|$
  • $\overrightarrow{C}\left|\begin{array}{c}{C}_x=K.y\\ C_y=0\end{array}\right|$ où K est une constante correspondant à la pression de l'eau.
• Face 2: $x=\alpha .y$
  • $\overrightarrow{n}\left|\begin{array}{c}{n}_x\\ n_y\end{array}\right|$
  • $\overrightarrow{C}\left|\begin{array}{c}{C}_x=0\\ C_y=0\end{array}\right|$ car la pression atmosphérique est très faible et donc négligée.
• Face 3 : $Y=L$
  • $\overrightarrow{n}\left|\begin{array}{c}0\\ 1\end{array}\right|$
  • $\overrightarrow{C}$ n’est pas connu.

Exemple de contraintes limites sur une poutre encastrée

1 et 2 sont 2 matériaux soudés. La section carrée est de longueur 2a ; le volume correspond aux deux matériaux ; la sollicitation extérieure est $\overrightarrow{T}$ en M.

• Contraintes pour les faces suivantes:

• • $x=0$

$\overrightarrow{n}=\left|\begin{array}{c}-1\\ 0\\ 0\end{array}\right|$

• • $\overrightarrow{C}=?$
• Contraintes pour les faces:

• • $\begin{array}{c}y=\pm a\\ z=\pm a\end{array}$

en y : $\overrightarrow{n}\left|\begin{array}{c}0\\ \pm 1\\ 0\end{array}\right|$ en z : $\overrightarrow{n}\left|\begin{array}{c}0\\ 0\\ \pm 1\end{array}\right|$

• • $\overrightarrow{C}=\overrightarrow{0}$
  • Conséquences sur $\tilde{\sigma }$: $\tilde{\sigma }.\overrightarrow{n}=\overrightarrow{C}$

Sur les faces concernées on a: $\tilde{\sigma }.\overrightarrow{n}=\overrightarrow{0}\Rightarrow \left(\begin{array}{ccc}{\sigma }_x& {\sigma }_{x}y& {\sigma }_{x}z\\ 0& {\sigma }_y& {\sigma }_{y}z\\ 0& 0& {\sigma }_z\end{array}\right)\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)$

d'où $\begin{array}{c}{\sigma }_{x}y=0\\ {\sigma }_y=0\\ {\sigma }_{z}y=0\end{array}$

On ne peut rien dire d’autre sur les autres termes de $\tilde{\sigma }$

• Contrainte sur la face $x=L$ :
  • $\overrightarrow{n}=\left|\begin{array}{c}0\\ 1\\ 0\end{array}\right|.\left|\begin{array}{c}1\\ 0\\ 0\end{array}\right|$

Cela correspond à l'effort $\overrightarrow{T}$ appliqué en un point. On va chercher à déterminer $\overrightarrow{C}$.

Théorème de Saint-Venant

Fin de l'exemple de la poutre

Il faut trouver une sollicitation dont les résultantes sont égales aux résultantes de $\overrightarrow{T}$ et qui permet de définir $\overrightarrow{C}$ Si $\sum \overrightarrow{R}=\overrightarrow{F}$ alors la contrainte de traction est la même dans les deux poutres.

$\int \overrightarrow{\tau }\mathrm{d}s=\overrightarrow{T}$

$\overrightarrow{\tau }$ sur y dont les moments des deux types de sollicitations sont égaux.

• Face $x=L$
  • $\overrightarrow{n}=\left|\begin{array}{c}0\\ 1\\ 0\end{array}\right|$
  • $\overrightarrow{C}=\overrightarrow{\tau }$

$\overrightarrow{\tau }$ est réparti et constant sur toute la face et tel que $\int \overrightarrow{\tau }\mathrm{d}s=\overrightarrow{T}$

• Conséquences sur $\tilde{\sigma }$

$\left(\begin{array}{ccc}{\sigma }_x& {\sigma }_{x}y& {\sigma }_{x}z\\ 0& {\sigma }_y& {\sigma }_{y}z\\ 0& 0& {\sigma }_z\end{array}\right).\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ -\tau \\ 0\end{array}\right)$ d'où $\begin{array}{c}{\sigma }_x=0\\ {\sigma }_{x}y=-||\overrightarrow{\tau }||\\ {\sigma }_{x}z=\end{array}$

• Interface $y=0$.

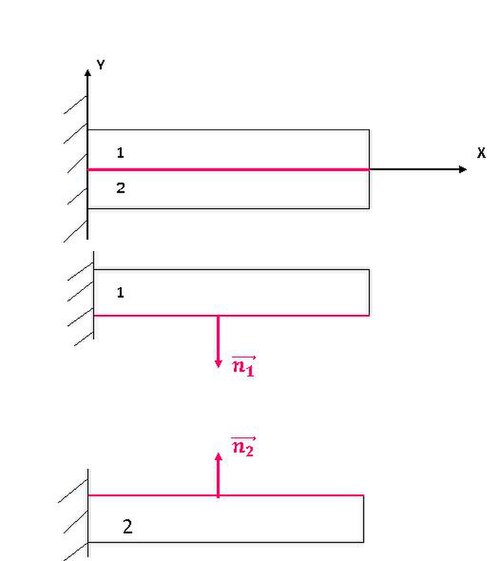
On ne connait pas $\overrightarrow{C}$ exercé par 1 sur 2 mais on sait que
​ $\overrightarrow{C^{1\to 2}}=-\overrightarrow{C^{2\to 1}}$ (loi d'action-réaction).

• Conséquence sur $\tilde{\sigma }$
  • $\widetilde{{\sigma }^1}=$ tenseur des contraintes dans le matériau 1.
  • $\widetilde{{\sigma }^2}=$ tenseur des contraintes dans le matériau 2.

$\begin{array}{c}\overrightarrow{C^{1\to 2}}=\widetilde{{\sigma }^2}.\overrightarrow{n^2}\\ \overrightarrow{C^{2\to 1}}=\widetilde{{\sigma }^1}.\overrightarrow{n^1}\end{array}\Rightarrow \widetilde{{\sigma }^2}.\overrightarrow{n^2}=-\widetilde{{\sigma }^1}.\overrightarrow{n^1}$

avec $\overrightarrow{n^1}=-\overrightarrow{n^2}$

On obtient la relation vectorielle : $\widetilde{{\sigma }^2}.\overrightarrow{n^1}=\widetilde{{\sigma }^1}.\overrightarrow{n^2}$ $\left(\begin{array}{ccc}{{\sigma }_x}^2& {{\sigma }_{x}y}^2& {{\sigma }_{x}z}^2\\ 0& {{\sigma }_y}^2& {{\sigma }_{y}z}^2\\ 0& 0& {{\sigma }_z}^2\end{array}\right).\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)=\left(\begin{array}{ccc}{{\sigma }_x}^1& {{\sigma }_{x}y}^1& {{\sigma }_{x}z}^1\\ 0& {{\sigma }_y}^1& {{\sigma }_{y}z}^1\\ 0& 0& {{\sigma }_z}^1\end{array}\right).\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)$ On obtient trois équations sur les composants: $\begin{array}{c}{{\sigma }_{x}y}^2={{\sigma }_{x}y}^1\\ {{\sigma }_y}^2={{\sigma }_y}^1\\ {{\sigma }_{y}z}^2={{\sigma }_{y}z}^1\end{array}$

Conclusion

Les conditions limites sur les contraintes concernent le vecteur contrainte qui est appliqué par l'extérieur sur le volume considéré.

Analyse des conditions aux limites

L’analyse des conditions aux limites consiste à traduire une sollicitation complexe à géométrie complexe en une condition limite (notée CL dans les exemples de ce cours) que l’on peut écrire mathématiquement « simplement » par un code élément fini.

Exemple :

​

CL en x=0 → $\overrightarrow{u}$(x=0)=$\overrightarrow{0}$

Quelles est la construction mécanique (technologique) utilisée pour l’encastrement ?

Si on a réalisé l’encastrement avec des équerres, le modèle $\overrightarrow{u}$=(x=0)$\overrightarrow{0}$n’est pas strictement représentatif.
​

Si on a réalisé l’encastrement avec une soudure , le modèle $\overrightarrow{u}$=(x=0)$\overrightarrow{0}$ est plus proche de la réalité.

On utilise le Principe de Saint Venant qui est démontré seulement pour l’élasticité.

(Attention : pas démontré en plasticité et faux pour les fluides.)

- Énoncé du principe :
​ Soit une distribution de forces agissant aux points M d’une surface $\overrightarrow{F}$(M)comprise sur la surface SModèle:Exp du système étudié.

Les éléments de réduction de cette distribution forment un torseur.
​ $\{\begin{array}{c}\overrightarrow{F}r\\ \overrightarrow{M}p\overrightarrow{F}r\end{array}$ Si on remplace $\overrightarrow{F}$(M) par un autre centre de distribution ${\overrightarrow{F}}^{\prime }$(M) , toujours appliqué sur la même surface SModèle:Exp, telle que le torseur de ${\overrightarrow{F}}^{\prime }$en P est égal au torseur de $\overrightarrow{F}$ en P. Les autres conditions aux limites restent inchangées. Alors, dans toutes régions de V « suffisamment » éloignée de S , les champs de contraintes et le déplacements sont « pratiquement » (pour la pratique) inchangés.

​

Même $\tilde{\sigma }$ et $\overrightarrow{u}$qu'avec les équerres dans la zone entourée en vert.
​ $\overrightarrow{F}$₁ et $\overrightarrow{F}$₂ même résultante et même moment qu'avec $\overrightarrow{F}$(M) équerre.
​ On peut s’éloigner d’une distance de même ordre de grandeur que S’ et on va retrouver des champs qui sont modifiés de – de 10%.
​ Exemple d'une plaque percée :
​

Principe de Saint Venant utile pour simplifier les CL mais ne donne pas d’information sur ce qui se passe au niveau de la surface des CL. Comment le principe de Saint Venant s’utilise avec un torseur des contraintes ?

Sur la surface S

On a :

$\tilde{\sigma }\overrightarrow{n}=d\overrightarrow{F}$

$\overrightarrow{n}$ vecteur normal à s

$\overrightarrow{C}=\tilde{\sigma }\overrightarrow{n}$

$d\overrightarrow{F}=\tilde{\sigma }\overrightarrow{n}$dS

Torseur résultat sur S

$\overrightarrow{F}r=\underset{S}{\iint }\tilde{\sigma }\overrightarrow{n}$dS
$\overrightarrow{M}\overrightarrow{R}/P=\underset{S}{\iint }\overrightarrow{PM}\wedge \tilde{\sigma }\overrightarrow{n}$dS
Exemple :
​

Force répartie pour fléchir une poutre dont la résultante est $\overrightarrow{T}$
​

CL : $\overrightarrow{C}$=?

$\underset{S}{\iint }\overrightarrow{C}$ dS = $\overrightarrow{T}$

Autre exemple :
​

$\overrightarrow{R}=\overrightarrow{0}$ → $\underset{S}{\iint }\tilde{\sigma }\overrightarrow{n}$ dS=0
$\overrightarrow{M}\overrightarrow{F}/0=\overrightarrow{C}$ouple → $\underset{S}{\iint }\overrightarrow{OM}\wedge \tilde{\sigma }\overrightarrow{n}$ dS = $\overrightarrow{C}$ouple
Conclusion : On sait résoudre ce problème d’élasticité.