Conduction thermique/Équation de la chaleur

Équation de la chaleur

L'équation de la chaleur s'écrit en toute généralité :Modèle:Encadreoù

T est la température ;
λ est la conductivité thermique ;
c_v est la capacité thermique massique à volume constant ;
ρ est la masse volumique ;
$\nabla$ est nabla et ${\vec{\nabla}}^{2}$ est le laplacien ;
p est la puissance volumique dégagée (par exemple dans le cas d'un résistor, p est la puissance dissipée par effet Joule).

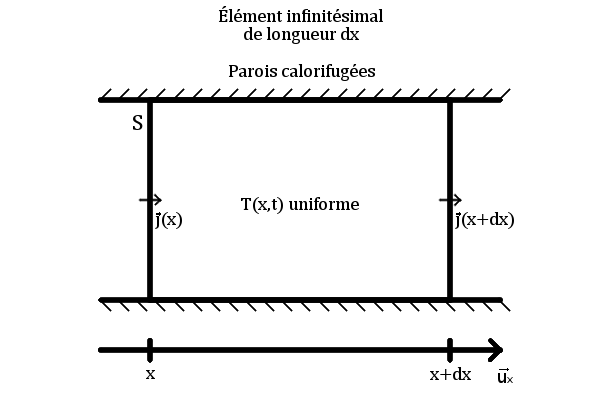
On applique le premier principe à un petit élément de longueur $d x$ , en considérant que les échanges thermiques :

$d U = \partial Q + P d t$

$P d t$ est l'énergie dégagée pendant un temps $d t$

Dans le cas d'une phase condensée (on écrit alors que c_v = c = c_p) ou un gaz parfait :

$d U = m * c_{v} d T$

Donc par définition de j, densité de flux thermique

$m * c_{v} \frac{\partial T}{\partial t} d t = j (x) S d t - j (x + d x) S d t + P d t$

où S est la surface.

Par définition de la différentielle et par simplification par $d t$

$\frac{\partial T}{\partial t} = - \frac{S}{m * c_{v}} \frac{\partial j}{\partial x} d x + \frac{P}{m * c_{v}}$

Par définition de la masse volumique $ρ = \frac{m}{\partial V}$ et du petit volume considéré $\partial V = S d x$

De plus la loi de Fourier donne $\vec{j} = - λ \vec{\nabla} T$ , où $\vec{\nabla} T$ est le gradient de la température qui sécrit en une dimension :

$\vec{\nabla} T = \frac{\partial T}{\partial x}$

Finalement, en notant $p d t$ l'énergie volumique dégagée pendant un temps $d t$ :

$\frac{\partial T}{\partial t} = \frac{λ}{ρ c_{v}} \frac{\partial^{2} T}{\partial x^{2}} + \frac{p}{ρ c_{v}}$

On peut alors généraliser de la même façon à trois dimensions.