Thermodynamique chimique/Lois de la thermochimie

Les lois de la thermochimie sont en particulier:

• la Loi de Hess (1840) qui est une loi de conservation des chaleurs. H et U étant des fonctions d'état, alors les chaleurs de réaction Q_P = ΔH et Q_V = ΔU ne dépendent que de l'état initial et de l'état final.
• les formules de Kirchhoff qui permettent de calculer la chaleur de réaction à une température T quand on a la valeur à une autre température (en particulier, les tables de données donnent ΔH sous 1 bar à la température de Modèle:Unité.).

Cycles de Hess - enthalpie ΔH

Il est très simple de calculer la variation d'enthalpie ΔH d'une réaction quelconque en faisant un cycle où interviennent des réactions connues. Comme l'enthalpie est une fonction d'état, ses variations ne dépendent pas du chemin suivi puisqu'elles ne dépendent que de l'état final et de l'état initial.

Exemple 1 : combustion du méthane

Considérons la réaction de combustion du méthane $\mathrm{C}{\mathrm{H}}_{\mathrm{4}\mathrm{(}\mathrm{g}\mathrm{)}}$, effectuée à T sous la pression standard p°. Le bilan de cette réaction est:

$\mathrm{C}{\mathrm{H}}_{\mathrm{4}\mathrm{(}\mathrm{g}\mathrm{)}}\mathrm{+}\mathrm{2}{\mathrm{O}}_{\mathrm{2}\mathrm{(}\mathrm{g}\mathrm{)}}\mathrm{=}\mathrm{C}{\mathrm{O}}_{\mathrm{2}\mathrm{(}\mathrm{g}\mathrm{)}}\mathrm{+}\mathrm{2}{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{(}\mathrm{l}\mathrm{i}\mathrm{q}\mathrm{)}}$.

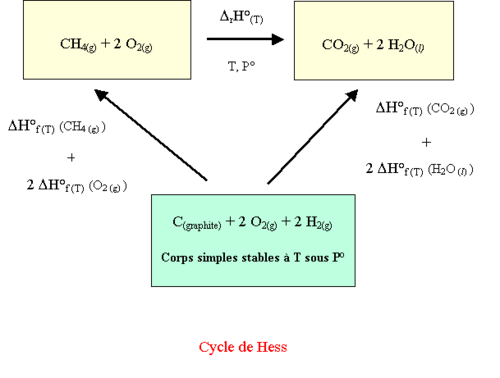
Il est possible de construire un cycle de Hess mettant en jeu la réaction précédente et des transformations impliquant les corps simples stables dans les conditions standard à T. Ce cycle est visualisé sur la figure suivante :

Les transformations impliquant les corps simples correspondent aux réactions de formations des constituants mis en jeu dans la réaction de combustion. Comme l'enthalpie est une fonction d'état, ses variations ne dépendent pas du chemin suivi puisqu'elles ne dépendent que de l'état final et de l'état initial. On obtient :

$\mathrm{\Delta }H=\mathrm{\Delta }H(\mathrm{C}{\mathrm{O}}_{\mathrm{2}})+2.\mathrm{\Delta }H({\mathrm{H}}_{\mathrm{2}}\mathrm{O})-\mathrm{\Delta }H(\mathrm{C}{\mathrm{H}}_{\mathrm{4}})-2.\mathrm{\Delta }H({\mathrm{O}}_{\mathrm{2}})$.

Ceci peut s'écrire aussi:

$\mathrm{\Delta }H=\sum _i{\nu }_i.{\left(\mathrm{\Delta }{H}_i\right)}_f$.

où

${\left(\mathrm{\Delta }{H}_i\right)}_f$ est l'enthalpie de formation et ${\nu }_i$ les coefficients stœchiométriques, négatifs dans le cas d'un réactifs, positifs dans le cas d'un produit.

Remarque

Les valeurs des enthalpies standard de formation sont données dans les tables à la température de Modèle:Unité. Elles permettent de calculer l'enthalpie standard de réaction à Modèle:Unité. La relation de Kirchhoff permet ensuite le calcul à une température différente T.

Exemple 2 : combustion de CH₃COOH

Considérons la combustion de l'acide acétique CH₃COOH (ou acide éthanoïque), se déroulant sous la pression standard et à la température 298 K. Le bilan de cette réaction est:

CH₃COOH_(l) + 2O_{2 (g)} = 2CO_{2 (g)} + 2H₂O_(l) (0)

On peut en fait voir cette réaction comme la composition de deux bilans de réactions (1) et (2):

CH₃COOH_(l) + 2O_{2 (g)} = 2C_(graphite) + 2H_{2 (g)} + 3O_{2 (g)} (1)

2C_(graphite) + 2H_{2 (g)} + 3O_{2 (g)} = 2CO_{2 (g)} + 2H₂O_(l) (2)

Ce qui s'écrit encore:

CH₃COOH_(l) = 2C_(graphite) + 2H_{2 (g)} + O_{2 (g)} (1)

2C_(graphite) + 2H_{2 (g)} + 3O_{2 (g)} = 2CO_{2 (g)} + 2H₂O_(l) (2)

On peut, de plus, décomposer (2) en deux réactions (2') et (2")

2C_(graphite) + 2O_{2 (g)} = 2CO_{2 (g)} (2')

2H_{2 (g)} + O_{2 (g)} = 2H₂O_(l) (2")

On peut donc voir (0) comme étant la succession de (1) puis (2')+(2"). Comme la variation d'enthalpie ne dépend pas du chemin suivi (fonction d'état), on peut écrire:

$\mathrm{\Delta }h(0)=\mathrm{\Delta }h(1)+\mathrm{\Delta }h(2)=\mathrm{\Delta }h(1)+\mathrm{\Delta }h(2^{\prime })+\mathrm{\Delta }h(2^{″})$

où h est l'enthalpie molaire en J/mol.

la notation $h_{298}^0$ veut dire enthalpie molaire standard ( i.e. sous 1 bar, notée ^O ) à la température de 298 K.

Or, on peut remarquer que la réaction (1) est l'exacte opposée de la réaction de formation de CH₃COOH, (2') la formation de deux moles de CO₂ et (2") la formation de deux moles de H₂O. On a donc:

$\mathrm{\Delta }h(1)=-{\left(\mathrm{\Delta }{h}_{(C{H}_{3}COOH)}\right)}_f$

$\mathrm{\Delta }h(2^{\prime })={\left(\mathrm{\Delta }{h}_{(2C{O}_2)}\right)}_f=2.{\left(\mathrm{\Delta }{h}_{(C{O}_2)}\right)}_f$

$\mathrm{\Delta }h(2^{″})={\left(\mathrm{\Delta }{h}_{(2H_{2}O)}\right)}_f=2.{\left(\mathrm{\Delta }{h}_{(H_{2}O)}\right)}_f$

On en déduit finalement que

$\mathrm{\Delta }h=-{\left(\mathrm{\Delta }{h}_{(C{H}_{3}COOH)}\right)}_f+2.{\left(\mathrm{\Delta }{h}_{(C{O}_2)}\right)}_f+2.{\left(\mathrm{\Delta }{h}_{(H_{2}O)}\right)}_f$

De manière générale, on peut écrire:
Modèle:Encadre où:

${\left(\mathrm{\Delta }{h}_{T,(A_i)}\right)}_f$ est l'enthalpie molaire de formation du composé $A_i$ à la température T;

${\nu }_i$ est le coefficient stœchiométrique du composé $A_i$, négatif dans le cas d'un réactifs, positif dans le cas d'un produit.

Dans les conditions standard ( 1 bar ) , on aura:

$\mathrm{\Delta }{h}_T^0=\sum _i{\nu }_i.{\left(\mathrm{\Delta }{h}_{T,(A_i)}^0\right)}_f$,

${\left(\mathrm{\Delta }{h}_{T,(A_i)}^0\right)}_f$ est l'enthalpie standard molaire de formation du composé $A_i$ à la température T

Formules de Kirchhoff

La «loi» de Kirchhoff permet de calculer l'enthalpie standard de réaction à la température T₁, connaissant l’enthalpie standard de réaction à la température T. Pour cela, on dit que l'enthalpie de réaction à la température T₁ est équivalente selon deux chemins différents (car l'enthalpie est une fonction d'état):

• Le chemin direct
• Porter les réactifs à la température T, effectuer la réaction, puis porter les produits à la température T₁

Petits rappels:

On peut définir plusieurs capacités calorifiques:

• La capacité calorifique ( notée C majuscule ) de l’objet étudié (par exemple un cube de laiton)
• La capacité calorifique spécifique qui est calculée pour une mole de matière ( notée c minuscule ) et qui aura les unités J.mol^-1.K^-1
• La chaleur massique qui est calculée pour un kg de matière ( notée c minuscule ) et qui aura les unités J.kg^-1.K^-1
• $\mathrm{P}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{u}\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{:}dV=0,{\mathrm{d}}^{\prime }\mathrm{o}\stackrel{`}{\mathrm{u}}\delta q=c_v.dT+l.dV=c_v.dT\mathrm{o}\stackrel{`}{\mathrm{u}}q=Q/N\mathrm{e}\mathrm{n}\mathrm{J}\mathrm{.}\mathrm{m}\mathrm{o}{\mathrm{l}}^{\mathrm{-}\mathrm{1}}$
• $\mathrm{P}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{u}\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{:}dP=0,{\mathrm{d}}^{\prime }\mathrm{o}\stackrel{`}{\mathrm{u}}\delta q=c_p.dT+h.dP=c_p.dT\mathrm{e}\mathrm{n}\mathrm{J}\mathrm{.}\mathrm{m}\mathrm{o}{\mathrm{l}}^{\mathrm{-}\mathrm{1}}$

avec

$C_v=\frac{\partial U}{\partial T}\mathrm{e}\mathrm{t}{C}_p=\frac{\partial H}{\partial T}$

ou

$c_v=\frac{\partial u}{\partial T}\mathrm{e}\mathrm{t}{c}_p=\frac{\partial h}{\partial T}$

On se place dans le cas d'une transformation isobare. On a alors:

$dH=\delta Q=C_p.dT$

Alors la variation d'enthalpie pour porter les réactifs de T₁ à T vaut:

$\mathrm{\Delta }H=\underset{T_1}{\overset{T}{\int }}{C}_p(reactifs)dT$

et l'enthalpie pour porter les produits de T à T₁ vaut:

$\mathrm{\Delta }H=\underset{T}{\overset{T_1}{\int }}{C}_p(produits)dT$

On a donc:

$\mathrm{\Delta }{H}_{T_1}=\mathrm{\Delta }{H}_T+\underset{T}{\overset{T_1}{\int }}(C_p(produits)-C_p(reactifs)).dT$

avec des grandeurs molaires, on aura:

$\mathrm{\Delta }{h}_{T_1}=\mathrm{\Delta }{h}_T+\underset{T}{\overset{T_1}{\int }}(c_p(produits)-c_p(reactifs)).dT$

sous 1 bar:

$\mathrm{\Delta }{H}_{T_1}^0=\mathrm{\Delta }{H}_T^0+\underset{T}{\overset{T_1}{\int }}(C_p(produits)-C_p(reactifs)).dT$

Avec:

$C_p(reactifs)=\sum _{reactifs}{\nu }_i.c_{p_i}$

$C_p(produits)=\sum _{produits}{\nu }_i.c_{p_i}$

on peut aussi écrire Modèle:Encadre

transformation isochore

Dans le cas d'une transformation isochore, on a en fait:

$dU=\delta Q=C_{v}dT$

La loi de Kirchhoff portera alors sur l'énergie interne:

${\mathrm{\Delta }}_r{U}_{T_1}^0={\mathrm{\Delta }}_r{U}_T^0+\underset{T}{\overset{T_1}{\int }}(C_v(produits)-C_v(reactifs)).dT$

Modèle:Encadre

Notez que C_p et C_v peuvent dépendre de la température.

Exemple

Le bilan de la réaction de formation de l'eau liquide entre Modèle:Unité (273K) et Modèle:Unité (373 K) s'écrit:

$H_{2(g)}+\frac{1}{2}{O}_{2(g)}=H_{2}O{}_{(l)}$

Dans les tables thermodynamiques, on trouve généralement l'enthalpie standard molaire de formation de l'eau liquide à 298K (Modèle:Unité). Si on veut calculer l'enthalpie standard molaire de formation à 350K, la loi de Kirchoff nous dit que dans le cas d'une transformation isobare:

$Q_P(350K)={\left(\mathrm{\Delta }{H}_{350}^0\right)}_f={\left(\mathrm{\Delta }{H}_{298}^0\right)}_f+\underset{298}{\overset{350}{\int }}(C_p(H_{2}O)-C_p(H_2)-\frac{1}{2}.C_p(O_2)).dT$