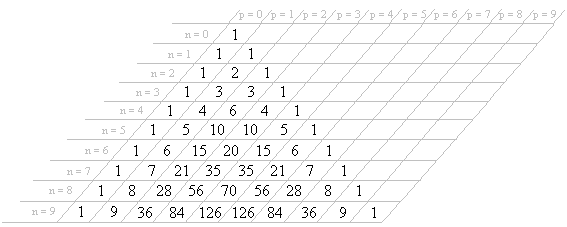Expressions algébriques/Identités remarquables

Modèle:Chapitre Nous savons que les trois Identités remarquables de base jouent un rôle important dans la transformation d'expressions algébriques. Nous allons donc, dans ce chapitre, compléter la liste avec d'autres identités remarquables pour pouvoir disposer de plus de puissance de calcul. La vérification de la justesse de ces identités remarquables est élémentaire et nous la laisserons donc au lecteur à titre d'exercice.

Identités remarquables du second degré

Ce sont les identités remarquables que nous connaissons bien :

$(a+b{)}^2=a^2+2ab+b^2$

$(a-b{)}^2=a^2-2ab+b^2$

$a^2-b^2=(a-b)(a+b)$

auxquelles nous pouvons ajouter :

$(a+b+c{)}^2=a^2+b^2+c^2+2ab+2ac+2bc$

Identités remarquables du troisième degré

Nous avons :

$(a+b{)}^3=a^3+3a^{2}b+3a{b}^2+b^3$

$(a-b{)}^3=a^3-3a^{2}b+3a{b}^2-b^3$

$a^3-b^3=(a-b)(a^2+ab+b^2)$

$a^3+b^3=(a+b)(a^2-ab+b^2)$

Identités remarquables du quatrième degré

Nous avons :

$(a+b{)}^4=a^4+4a^{3}b+6a^2{b}^2+4a{b}^3+b^4$

$(a-b{)}^4=a^4-4a^{3}b+6a^2{b}^2-4a{b}^3+b^4$

$a^4-b^4=(a-b)(a+b)(a^2+b^2)$

Identités remarquables du cinquième degré

Nous avons :

$(a+b{)}^5=a^5+5a^{4}b+10a^3{b}^2+10a^2{b}^3+5a{b}^4+b^5$

$(a-b{)}^5=a^5-5a^{4}b+10a^3{b}^2-10a^2{b}^3+5a{b}^4-b^5$

$a^5-b^5=(a-b)(a^4+a^{3}b+a^2{b}^2+a{b}^3+b^4)$

$a^5+b^5=(a+b)(a^4-a^{3}b+a^2{b}^2-a{b}^3+b^4)$

Identités remarquables du nième degré

Quelle que soit la valeur de $n$ (paire ou impaire), le développement de la formule générale $a^n-b^n$est la suivante:

$a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}{b}^2+\cdots +a^2{b}^{n-3}+a{b}^{n-2}+b^{n-1})$

$a^n-b^n=(a-b)\times \sum _{p=1}^n{a}^{n-p}\times b^{p-1}$

Si l'exposant $n$ est impair, la formule générale $a^n+b^n$ existe. Son développement est le suivant :

$a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}{b}^2-a^{n-4}{b}^3+\cdots +a^2{b}^{n-3}-a{b}^{n-2}+b^{n-1})$

$a^n+b^n=(a+b)\times \sum _{p=1}^n{a}^{n-p}\times (-b{)}^{p-1}$

En ce qui concerne les identités remarquables de la forme $(a\pm b{)}^n$, nous considérerons le tableau :

Pour construire ce tableau, appelé « triangle de Pascal », nous remarquerons que chaque nombre du tableau est la somme des deux nombres situés immédiatement au-dessus :

Si nous prenons une identité que nous avons vu plus haut comme :

$(a+b{)}^4=a^4+4a^{3}b+6a^2{b}^2+4a{b}^3+b^4$

nous remarquons que les coefficients respectifs des termes du second membre sont :

$1,4,6,4,1$

qui, comme nous pouvons le constater, correspondent à la ligne $n=4$ du triangle de Pascal.

Il en est de même pour toutes ces identités remarquables.

Par exemple, en se basant sur la ligne $n=7$, on obtient l'identité remarquable suivante :

$(a+b{)}^7=a^7+7a^{6}b+21a^5{b}^2+35a^4{b}^3+35a^3{b}^4+21a^2{b}^5+7a{b}^6+b^7$

On remarquera que les puissances respectives de $a$ croissent et que les puissances respectives de $b$ décroissent.

S'il y a un signe $-$ dans le premier membre, on alternera les $+$ et les $-$ ainsi :

$(a-b{)}^7=a^7-7a^{6}b+21a^5{b}^2-35a^4{b}^3+35a^3{b}^4-21a^2{b}^5+7a{b}^6-b^7$

Autrement dit, on mettra un signe $-$ devant les puissances impaires de $b$.

Modèle:Bas de page